A red-black tree is a kind of self-balancing binary search tree where each node has an extra bit, and that bit is often interpreted as the color (red or black). These colors are used to ensure that the tree remains balanced during insertions and deletions. Although the balance of the tree is not perfect, it is good enough to reduce the searching time and maintain it around O(log n) time, where n is the total number of elements in the tree. This tree was invented in 1972 by Rudolf Bayer. It must be noted that as each node requires only 1 bit of space to store the color information, these types of trees show identical memory footprints to the classic (uncolored) binary search tree.
5 rules in RBT1. Every node has a color either red or black
2. The root of the tree is always black
3. There are no two adjacent red nodes (Ared node cannot have a red parent or red child)
4. Every path from a node (including root) to any of its descendants NULL nodes has the same number of black nodes.
5. All leaf nodes are black nodes
| Algorithm | Time Complexity |
|---|---|
| Search | O(log n) |
| Insert | O(log n) |
| Delete | O(log n) |
The goal of the insert operation is to insert key K into tree T, maintaining T's red-black tree properties. A special case is required for an empty tree. If T is empty, replace it with a single black node containing K. This ensures that the root property is satisfied.
If T is non-empty tree, then weuse the BST insert algorithm to add K to the tree, color the node containing K red, and restore red-black tree properties if necessary
Recall that the BST insert algorithm always adds a leaf node. Because we are dealing with a non-empty red-black tree, adding a leaf node will not affect T's satisfaction of the root property. Moreover, adding a red leaf node will not affect T's satisfaction of the black property. However, adding a red leaf node may affect T's satisfaction of the red property, so we will need to check if that is the case and, if so, fix it (step 3). In fixing a red property violation, we will need to make sure that we don't end up with a tree that violates the root or black properties.
For step 3 for inserting into a non-empty tree, what we need to do will depend on the color of K's parent. Let P be K's parent. We need to consider two cases:
1. K's parent P is Black
If K's parent P is black, then the addition of K did not result in the red property being violated, so there's nothing more to do.
2. K's parent P is Red
If K's parent P is red, then P now has a red child, which violates the red property. Note that P's parent, G, (K's grandparent) must be black (why?). In order to handle this double-red situation, we will need to consider the color of G's other child, that is, P's sibling, S. (Note that S might be null, i.e., G only has one child and that child is P.)
2-1. P's sibiling S is black or null
If P's sibling S is black or null, then we will do a trinode restructuring of K (the newly added node), P (K's parent), and G (K's grandparent). To do a restructuring, we first put K, P, and G in order; let's call this order A, B, and C. We then make B the parent of A and C, color B black, and color A and C red. We also need to make sure that any subtrees of P and S (if S is not null) end up in the appropriate place once the restructuring is done.
Once a restructuring is done, the double-red situation has been handled and there's nothing more to do.
2-2. P's sibling S is red
If P's sibling S is red, then we will do a recoloring of P, S, and G: the color of P and S is changed to black and the color of G is changed to red.
Recoloring does not affect the black property of a tree: the number of black nodes on any path that goes through P and G is unchanged when P and G switch colors (similarly for S and G). But, the recoloring may have introduced a double-red situation between G and G's parent. If that is the case, then we recursively handle the double-red situation starting at G and G's parent (instead of K and K's parent).
Below image is an RBT insertion diagram.
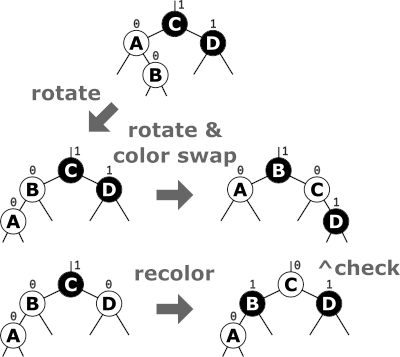
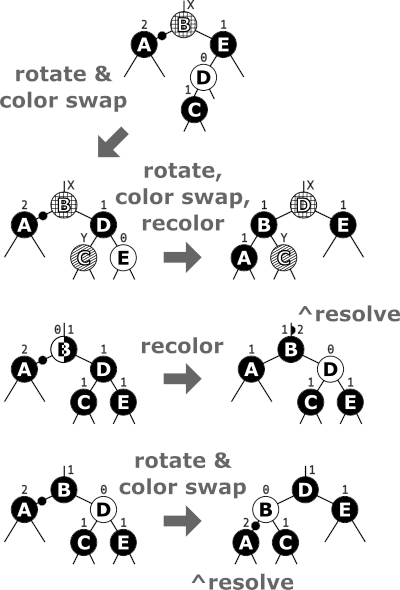
Like Insertion, recoloring and rotations are used to maintain the Red-Black properties. In the insert operation, we check the color of the uncle to decide the appropriate case. In the delete operation, we check the color of the sibling to decide the appropriate case. The main property that violates after insertion is two consecutive reds. In delete, the main violated property is, change of black height in subtrees as deletion of a black node may cause reduced black height in one root to leaf path. Deletion is a fairly complex process. To understand deletion, the notion of double black is used. When a black node is deleted and replaced by a black child, the child is marked as double black. The main task now becomes to convert this double black to single black.
1. Perform standard BST delete. When we perform standard delete operation in BST, we always end up deleting a node which is an either leaf or has only one child (For an internal node, we copy the successor and then recursively call delete for successor, successor is always a leaf node or a node with one child). So we only need to handle cases where a node is leaf or has one child. Let v be the node to be deleted and u be the child that replaces v (Note that u is NULL when v is a leaf and color of NULL is considered as Black).
2. If either K or P is red
we mark the replaced child as black (No change in black height). Note that both K and P cannot be red as P is parent of K and two consecutive reds are not allowed in red-black tree.
3. If both K and P are Black
3-1 Color K as double black
Now our task reduces to convert this double black to single black. Note that If P is leaf, then K is NULL and color of NULL is considered black. So the deletion of a black leaf also causes a double black.
<3.2>3-2-1 If sibiling is black and at least one of fibiling's children is red, perform rotation(s). There are three cases depending on whether sibling and parent are on left or right.3-2-1-1 Left Left case
3-2-1-2 Left Right case
3-2-1-3 Right Right case
3-2-2 If sibling is black and its both children are black
In this case, if parent was red, then we didn't need to recur for parnet, we can simply make it black (red + double black = single black)
3-2-3 If sibling is red, perform a rotation to move old sibling up, recolor the old sibling and parent. The new sibling is always black. This mainly converts the tree to black sibling case (by roation) and leads to 2 other cases
3-2-3-1 Left case
3-2-3-2 Right case
3-3 If K is root, make it single bkack andreturn. In this process the black height of complete tree reduces by 1.
Below image is an RBT deletion diagram.
 Useful Sources
RBT Visualization
Geeks for Geeks RBT detailed explanation
Useful Sources
RBT Visualization
Geeks for Geeks RBT detailed explanation