Program Specification

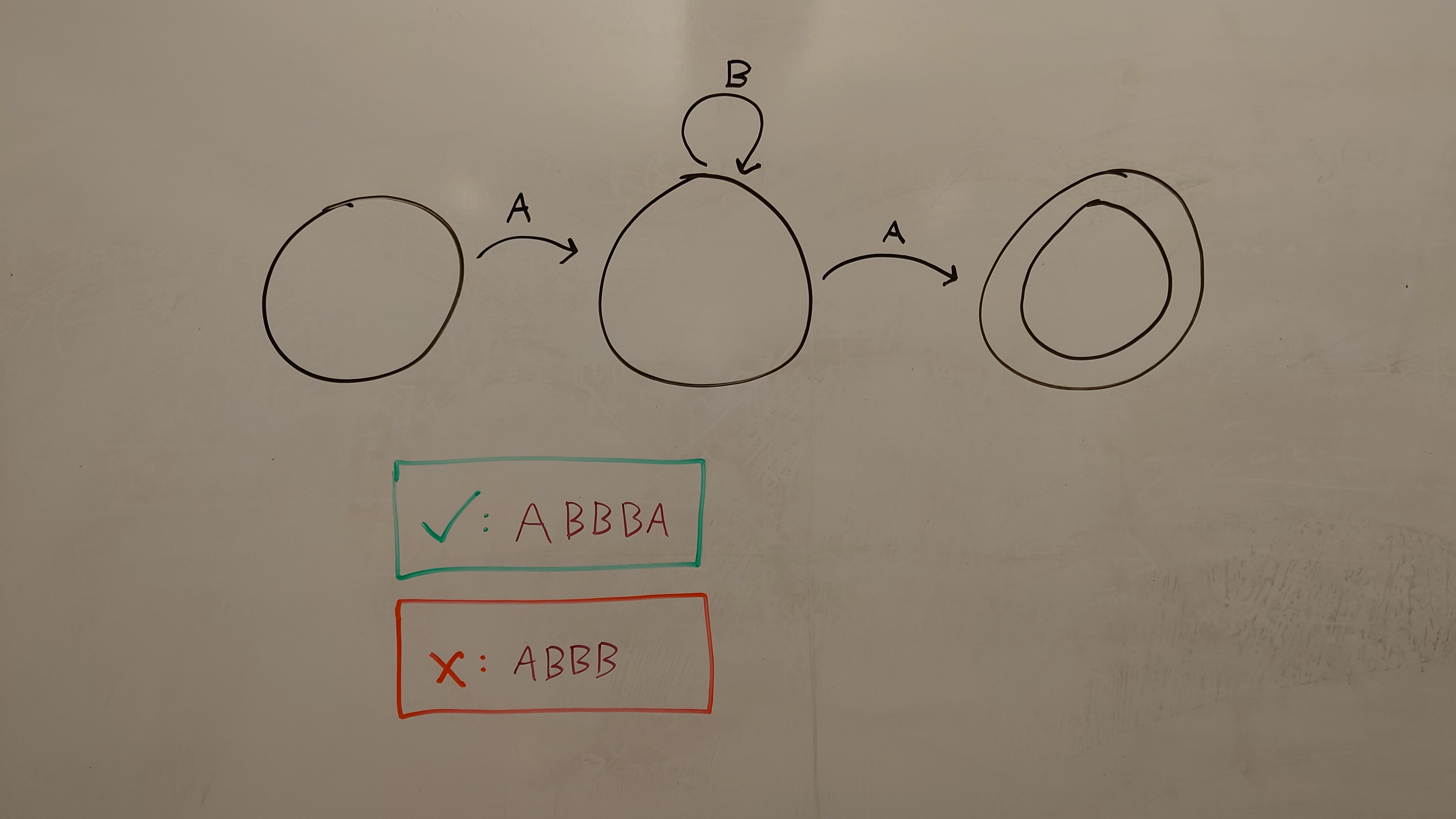
This page will use the automaton A1 as an example, shown below.

A deterministic finite automaton $M$ can be represented as a tuple $(Q, Σ, δ, q_{0}, F)$ , where $Q$ is the set of states, $Σ$ is the input alphabet, $δ : Q \times Σ \to Q$ is the transition relation, $q_{0}$ is the initial state, and $F \subseteq Q$ is the set of accepting states. For the purposes of this project, we assume that $Σ \subseteq {0, 1, A, B}$ ; this is a limit of our OCR implementation more than anything. The remaining tuple components are covered below.

State Specification

Our automata model represents states as integers, with a unique integer for each state, along with a special “zero” state that represents the failure case: all outgoing transitions from the zero state lead back to itself. Formally, $Q \subset Z \land \exists n . | Q | < n \land 0 \in Q$ .

We define a function $i s S t a t e : Z \to B$ , such that $\forall z \in Z . i s S t a t e (z) ⟺ z \in Q$ , and a function $i s A c c e p t i n g : Q \to B$ , such that $\forall q \in Q . i s A c c e p t i n g (q) ⟺ q \in F$ .

Concretely, these declarations correspond to the following in SMT-LIB2 for A1:

(define-fun is-state ((q Int)) Bool
    (and (< (- 1) q) (< q 4)))
	
(define-fun is-accepting ((q Int)) Bool
    (or (= q 3)))

as A1 has 3 defined states (so $q$ varies from 0 to 3), with the third state being the only accepting one.

We additionally declare the initial state $q_{0}$ as an uninterpreted constant for the synthesis procedure to find, with the constraints $q_{0} \neq 0 \land i s S t a t e (q_{0})$ . Concretely, these translate to:

(declare-fun IS () Int)
(assert (not (= 0 IS)))
(assert (is-state IS))

Transition Specification

Determining the transition relation $δ$ is the primary objective of our synthesis procedure. We define it as an uninterpreted function:

(declare-fun T (Int String) Int)

We start with the general constraint that all transitions from valid states must go to valid states, that is, $\forall q \in Q, s \in Σ . δ (q, s) \in Q$ :

(assert (forall ((q Int) (symb String))
            (=> (is-state q)
                (is-state (T q symb)))))

We constrain the zero state such that no transitions can leave, $\forall s \in Σ . δ (0, s) = 0$ :

(assert (forall ((symb String))
            (= 0 (T 0 symb))))

We then assert all defined transitions from the annotated image; for an example transition 1 --> 2 [A], $δ (1, A) = 2$ . For A1, these transitions are concretely:

(assert (= 2 (T 1 "A")))
(assert (= 2 (T 2 "B")))
(assert (= 3 (T 2 "A")))

Finally, we assert all negative transitions. That is, any symbol not specified must go to the zero state. For the example 1 --> 2 [A], $\forall s \in Σ . s \neq A ⟹ δ (1, s) = 0$ . Concretely:

(assert (forall ((symb String))
            (=> (not (or (= symb "A")))
                (= 0 (T 1 symb)))))
(assert (forall ((symb String))
            (=> (not (or (= symb "A") (= symb "B")))
                (= 0 (T 2 symb)))))
(assert (forall ((symb String))
            (=> (not (or false))
                (= 0 (T 3 symb)))))

Examples Specification

To handle our input examples, we first define an execution function that simulates the behavior of our automaton, $e x e c D f a : Q \times [Σ]_{k} \to B$ , where $[Σ]_{k}$ denotes a sequence of $k$ elements from $Σ$ . This function is defined recursively; when $k = 0$ , $e x e c D f a (q, []) ⟺ q \in F$ , otherwise $e x e c D f a (q, [s, \dots]) ⟺ e x e c D f a (δ (q, s), [\dots])$ . This can be concretely defined in SMT-LIB2 as:

(define-fun-rec exec-dfa ((q Int) (input String)) Bool
    (ite (= 0 (str.len input))
         (is-accepting q)
         (exec-dfa (T q (str.at input 0)) (str.substr input 1 (- (str.len input) 1))))) 

Then, each positive or negative example is just an assertion of this function starting on the initial state, $e x e c D f a (q_{0}, A B B B A) \land \neg e x e c D f a (q_{0}, A B B B)$ . Concretely:

(assert (exec-dfa IS "ABBBA"))
(assert (not (exec-dfa IS "ABBB")))