Program Specification

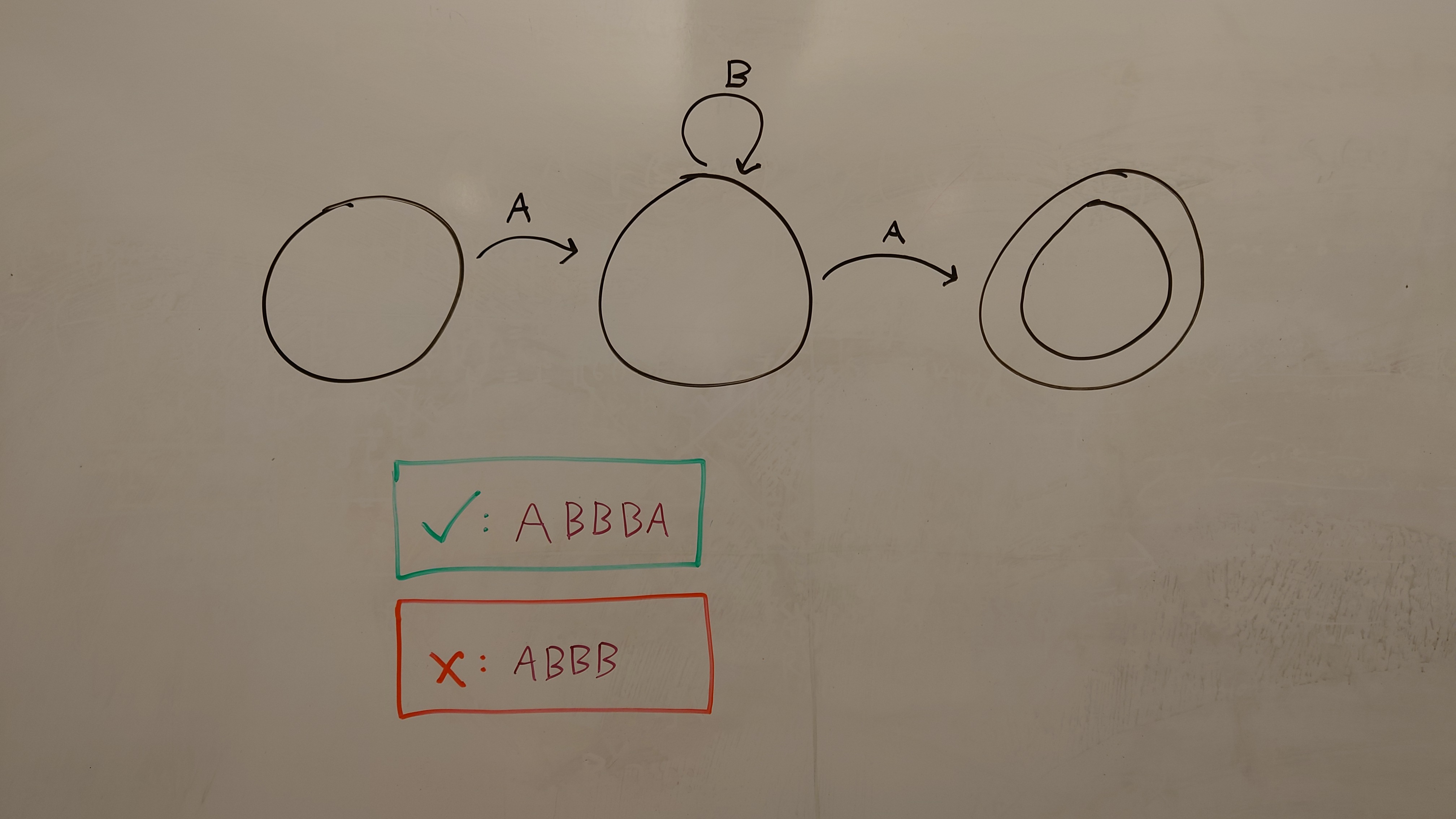
This page will use the automaton A1 as an example, shown below.

A deterministic finite automaton \(M\) can be represented as a tuple \((Q, \Sigma, \delta, q_0, F)\), where \(Q\) is the set of states, \(\Sigma\) is the input alphabet, \(\delta : Q \times \Sigma \to Q\) is the transition relation, \(q_0\) is the initial state, and \(F \subseteq Q\) is the set of accepting states. For the purposes of this project, we assume that \(\Sigma \subseteq \{ 0, 1, A, B \}\); this is a limit of our OCR implementation more than anything. The remaining tuple components are covered below.

State Specification

Our automata model represents states as integers, with a unique integer for each state, along with a special “zero” state that represents the failure case: all outgoing transitions from the zero state lead back to itself. Formally, \(Q \subset \mathbb{Z} \wedge \exists n.\; |Q| < n \wedge 0 \in Q\).

We define a function \(isState : \mathbb{Z} \to \mathbb{B}\), such that \(\forall z \in \mathbb{Z}.\; isState(z) \iff z \in Q\), and a function \(isAccepting : Q \to \mathbb{B}\), such that \(\forall q \in Q.\; isAccepting(q) \iff q \in F\).

Concretely, these declarations correspond to the following in SMT-LIB2 for A1:

(define-fun is-state ((q Int)) Bool
    (and (< (- 1) q) (< q 4)))
	
(define-fun is-accepting ((q Int)) Bool
    (or (= q 3)))

as A1 has 3 defined states (so \(q\) varies from 0 to 3), with the third state being the only accepting one.

We additionally declare the initial state \(q_0\) as an uninterpreted constant for the synthesis procedure to find, with the constraints \(q_0 \not= 0 \wedge isState(q_0)\). Concretely, these translate to:

(declare-fun IS () Int)
(assert (not (= 0 IS)))
(assert (is-state IS))

Transition Specification

Determining the transition relation \(\delta\) is the primary objective of our synthesis procedure. We define it as an uninterpreted function:

(declare-fun T (Int String) Int)

We start with the general constraint that all transitions from valid states must go to valid states, that is, \(\forall q\in Q, s\in\Sigma.\; \delta(q, s) \in Q\):

(assert (forall ((q Int) (symb String))
            (=> (is-state q)
                (is-state (T q symb)))))

We constrain the zero state such that no transitions can leave, \(\forall s\in\Sigma.\; \delta(0, s) = 0\):

(assert (forall ((symb String))
            (= 0 (T 0 symb))))

We then assert all defined transitions from the annotated image; for an example transition 1 --> 2 [A], \(\delta(1, A) = 2\). For A1, these transitions are concretely:

(assert (= 2 (T 1 "A")))
(assert (= 2 (T 2 "B")))
(assert (= 3 (T 2 "A")))

Finally, we assert all negative transitions. That is, any symbol not specified must go to the zero state. For the example 1 --> 2 [A], \(\forall s\in\Sigma.\; s \not=A \implies \delta(1, s) = 0\). Concretely:

(assert (forall ((symb String))
            (=> (not (or (= symb "A")))
                (= 0 (T 1 symb)))))
(assert (forall ((symb String))
            (=> (not (or (= symb "A") (= symb "B")))
                (= 0 (T 2 symb)))))
(assert (forall ((symb String))
            (=> (not (or false))
                (= 0 (T 3 symb)))))

Examples Specification

To handle our input examples, we first define an execution function that simulates the behavior of our automaton, \(execDfa : Q \times [\Sigma]_k \to \mathbb{B}\), where \([\Sigma]_k\) denotes a sequence of \(k\) elements from \(\Sigma\). This function is defined recursively; when \(k = 0\), \(execDfa(q,[]) \iff q\in F\), otherwise \(execDfa(q,[s,…]) \iff execDfa(\delta(q, s), […])\). This can be concretely defined in SMT-LIB2 as:

(define-fun-rec exec-dfa ((q Int) (input String)) Bool
    (ite (= 0 (str.len input))
         (is-accepting q)
         (exec-dfa (T q (str.at input 0)) (str.substr input 1 (- (str.len input) 1))))) 

Then, each positive or negative example is just an assertion of this function starting on the initial state, \(execDfa(q_0, ABBBA) \wedge \neg execDfa(q_0, ABBB)\). Concretely:

(assert (exec-dfa IS "ABBBA"))
(assert (not (exec-dfa IS "ABBB")))