CS368 Homework 7
Lec 1, Spring 2016
Due by 11:59 pm on Friday, May 6 (not accepted late)

Problems

You can get started with this homework by downloading this MATLAB script:

Complete ALL your work in MATLAB (in your homework7.m script and any functions you write. And, as with all homework assignments, your solution must use techniques discussed and covered in lecture and the on-line readings. You may not use MATLAB commands or constructs that have not been covered in lecture prior to the date of the release of the homework (or in the corresponding on-line readings).

Problem 1: (12 points) The Secant Method

In MATLAB, roots of functions are determined numerically (i.e., rather than symbolically) using numeric approximation algorithms. The Successive Numeric Approximation module describes Newton's Method for finding roots and you saw an implementation of the Bisection Method and Newton's Method in the Finding Roots example from the Successive Numeric Approximation handout. In this problem, you will implement a different numeric approximation algorithm for finding roots, the Secant Method. For the purposes of this problem, the function whose roots you will be finding is

This function is defined for you already (as a function handle named fctn) inside the provided homework7.m script.

1. (2 pts) Add code to your homework7.m script to plot f(x) from x = -6 to x = 8. Use the grid ON command and use the axis command to scale the plot so the y-axis ranges from -40 to 40.

A function which implements Newton's Method for finding roots has been implemented for you. Download the file

Newton's Method uses the first derivative of the function in its computation. In order for the newton function to work, it requires that 3 arguments be given to it: a function handle for the function for which we wish to find the root, a function handle for the function that computes the derivative of the function, and an initial guess for the location of the root.

2. (1 pt) Add code to your homework7.m script to define a function handle fctn_prime representing the derivative of f(x). The derivative f '(x) of the function f(x) is

   f '(x) = 3x² + 6x - 5 - 0.4 e^x

The Secant Method takes two initial guesses (x₀ and x₁), which must be distinct. It is very similar to Newton's method except that instead of using the derivative to find the slope of the tangent line at a point on the function, it estimates the slope of the tangent line by using the slope of the line between two nearby points on the function (i.e., the secant line).

The formula for determining the next guess (based on the two previous guesses) is:

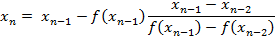
Starting with the initial guesses, x₀ and x₁, a new guess, x₂, is then obtained by finding where the line between the function values at the initial guesses intersects the x-axis; x₁ and x₂ are then used to compute a new guess, x₃, and the process repeats until the desired precision is reached (or two guesses in succession are identical).

3. (7 pts) Define a MATLAB function secant which takes 3 arguments:
   • func - a function handle for the function whose root is being determined
   • x0 - one initial guess, x₀
   • x1 - the second initial guess, x₁

   and returns a vector containing 2 values:

   • root - the value for the root obtained by implementing the secant method
   • iters - the number of iterations it took for the secant method to find the root (where the func(root) is within ε of 0 or two successive guesses are identical) or 50 (the maximum number of iterations the method will perform)

   The first line of the secant function should be:

   function [root, iters] = secant(func, x0, x1)

   The secant function should implement the following algorithm:

   1. if x₀ and x₁are the same value, quit with the error message "x0 and x1 must be distinct" (hint: use the error function)
      
      
   2. initially, curr is x₁ and prev is x₀
      while |func(curr)| > ε and # iterations < 50 and curr is not the same as prev
          compute a new guess using formula above
          update curr and prev

   Use ε = 10^-15 and don't forget to keep track of the number of iterations. Tip: look at the newton function and use it as a guide for the overall structure of step 2.

We now wish to compare the results we get using fzero, Newton's method, and the secant method for our function f(x).

4. (2 pts) Add the code below to your homework7.m script. This code compares the results of using fzero, newton, and secant using initial guesses ranging from -6 to 8. Note that the code should work as given.

   disp( 'method   : root (# iterations)')
   for guess = -6 : 8
       % the next line is used to visually separate the tests
       disp('--------------------------------------------------') 
       disp(['Initial guess: ' num2str(guess)])
       
       % calculate root and display results using each method
       % note: num2str(value, N) displays value to a maximum of N digits
       root_f = fzero(fctn, guess);
       disp(['fzero    : ', num2str(root_f, 20)])
       
       [root_n, iters_n] = newton(fctn, fctn_prime, guess);
       disp(['Newton''s : ', num2str(root_n, 20), '  (' num2str(iters_n), ')'])
       
       offset = 1;
       [root_s, iters_s] = secant(fctn, guess - offset, guess + offset);
       disp(['Secant   : ', num2str(root_s, 20), '  (' num2str(iters_s), ')'...
             '  offset: ' num2str(offset)])
   end
   

   Notice that in the code above, we obtain the two initial guesses needed by the Secant Method by adding and subtracting an offset to guess. We wish to also look at how the size of this offset affects the results we get from the Secant Method. Add code to the provided code above to compute and display the results when the Secant Method is called using offsets of 0.1, 0.01, and 0.001 (in addition to the offset of 1).

Problem 2: (8 points) Area between two curves

This problem deals with the two curves:

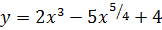
and

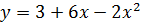
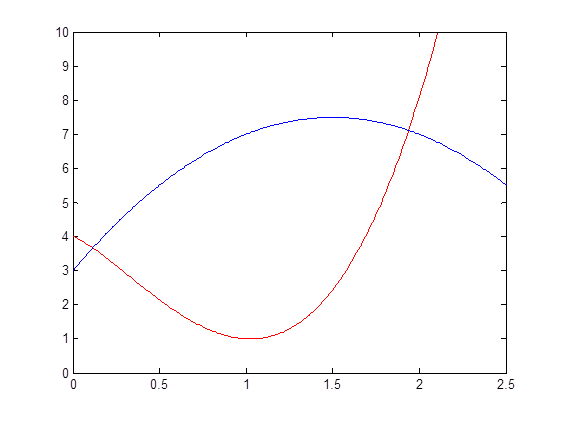
These curves are displayed in the next figure:

For this problem, you will need to make appropriate use of MATLAB's built-in fzero and integral functions. These MATLAB functions each take a function handle as one of their parameters. To receive full credit for this problem, you must use anonymous functions to represent the functions being passed as parameters (i.e., you may not define any functions in separate m-files). You will also need to add code to your homework7.m script which runs everything and displays the appropriate output.

1. Determine the x- and y-coordinates of the two intersection points. Make sure your script displays the coordinates of the intersection points.

2. Determine the area of the region between the two curves. Make sure your script displays this value. Note that you will need to use your intersection points from part a.

Handing in

Upload your m-files to your Dropbox in Learn@UW. See these instructions for uploading files to a Learn@UW Dropbox. The files you should upload are:

• homework7.m
• secant.m

In order for your work to be considered to have been turned in on-time, you must upload your files to your Learn@UW Dropbox by 11:59 pm Friday, May 6.