CS766 HW2

Yan Cao
Project 2 Report

 

Implementation steps

1. I created a java class called “CylindricalConvertion.java” to convert the example images to cylindrical views (saved as cXX.jpg). The central idea is realized by this part:

           for(int i=0;i<newWidth;i++){

               for(int j=0;j<newHeight;j++){

                    double newX=focus*Math.tan((i-newOriginx)/focus)+xc;

                   double newY=Math.sqrt((newX-xc)*(newX-xc)+focus*focus)*(j-newOriginy)/focus+yc;

                   int nearestX=Math.round((float)newX);

                   int nearestY=Math.round((float)newY);

                   bufferedImage.setRGB(i,j,originalImg.getRGB(nearestX,nearestY));

               }

           }

2. I used SIFTwin32 to generate key files (cXX.key).

3. Class “FeaturePairFinder.java” is used to find paired features between two photos. Because in the key files generated from SIFT, each feature point is described by a 128-dimention vector, for each point i in one graph, I used kNN (k=2) to find the 2 closest points (j, k), then I used “distance(i,j)/distance(j,k)>some cut value” to get the candidate pairs. It is realized by the function getPairs() in this class. The feature pairs are saved in a vector with the following format: “Xnode1 Ynode1 Xnode2 Ynode2”

4. RANSAC method is applied to get H between two adjacent graphs (m, n) so that the new coordinates of n can be got by doing the multiplication

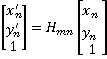                                 (1)

]T. The RANSAC is realized by the function getBestH() in class “Ransac.java”. So if we have N graphs, we get N H’s: H12, H23, …, HN-1,N, HN,1. Because we want to merge the N graphs to one graph, we need to get H12, H13, H14, …, H1,N, H1,1 so that we can convert the other graphs’ coordinates to graph 1’s coordinate system. Here H1i can be attained by using the following formula:

                  H1i= H12* H23*…*Hi-1,i        (2)

Thus, for graphs from 2 to N, use Equation 1 to do the transformation.

5. To make the centers of the first graph and the last graph on a horizontal line, I used a function shftY() to get a shift matrix S, where a=(centerY of the last graph - centerY of the first graph)/ (centerX of the last graph – centerX of the first graph). Then update H1i to S* H1i

 

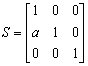
6. Calculate the coordinates of the 4 corner points for each graph. Compare them and get the minX, minY, maxX, maxY. The width of the new graph will be (maxX-minX) and the height is (maxY-minY). Then shift the coordinate by using x=x-minX, y=y-minY, so that the left top point moves to (0,0).

7. For each pixel (x’, y’) in the new graph, calculate the coordinates in all the original graphs by using 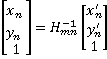     , and then judge if it is in the ranges of the original graphs. If in the range, pick the nearest pixel’s RGB value.

8. Blending. For each row i in the new graph, I used 2 arrays to save the RGB values. These 2 arrays are initiated with 0’s. If a pixel (i, j) is found in some graph, check if the jth element in the first array rgb1[j] == 0, if true, set rgb value to it, if not, set rgb to the jth element in the second array rgb2[j]. Then all overlapped parts can be found in the second array because they are split by 0’s. Then find each overlapped part and use feathering function a*rgb1[j]+(1-a)*rgb2[j] to get the blended rgb. 

Results

1.       Photos taken by me in front of the Bascom Hall.

 

The panorama graph generated (click to see full version):

The graph is also shown in pano viewer.

 

 

2.       The original graphs are the test graphs shown as following.

The panorama graph generated (click to see full version):

    

 

The graph is shown in pano viewer.

Discussion

From the result, we can clearly see the left part is obviously sheared. I think that it might be caused by the accumulative stitching. Notice that there are 19 graphs in total and the H for the19th graph is attained from a long multiplication, H12* H23*…*H18,19. So small values in positions (1,2) and (2,1) in H12, H23…. will cause big values in H1,19.

The good part is that I got a good result of feature match by using RANSAC. The overlapped parts are perfectly stitched. I got it by trying different parameters such as recursion times of RANSAC, cut value of feature pairs in feature selection(see step 3 in the first part).

 

Appended Discussion

I first generated the panorama from the sample graphs. I found there is a significant shear effect at the end of the panorama. Thus, I decide to change my algorithm a little bit to see if it can be solved in my new photos. Instead of using the coordinate system of the 1st graph, I choose the coordinate system of the graph in the middle. Since I have 20 consecutive photos (if we see the first one also the last one, we have 21 in total), I use the 11th graph as the basis, and transform the graphs on its left and right. From the result, we can see the shear effect is somewhats weakened.