CS766: Computer Vision
COURSE PROJECT
Project 1: High Dynamic Range Imaging
Ba-Quy Vuong
(baquy@cs.wisc.edu)
Department of Computer Sciences
UW-Madison
1. Introduction
Regular images only have 256 levels of brightness for each color channel. This is far below the viewing capability of human eyes. High dynamic range images have much higher dynamic range. However, traditional cameras are incapable of capturing those high dynamic range images. In this project, we aim to recover the high dynamic range images of a scene by using a regular camera. We first take pictures of that scene with various exposures. We then develop a computer program to combine these images and produce the high dynamic range image. In this report, we are going to discuss the implementations of two algorithms:
The High Dynamic Range Radiance Maps algorithm developed by Devebec and Malik [1] for recovering the high dynamic range image from a set of images taken by a regular camera.
The Median Bitmap Threshold (MBT) algorithm proposed by Ward [2] for aligning different images of the same scene.
2. The overall process
The process of recovering high dynamic images basically consists of three steps:
Image aligning: A series of images may not be well aligned due to human errors. For example, the camera may be shifted slightly when the photographer vibrates his hands. Even when taking pictures with tripod, some misalignment may also occur. If we do not align the original images before recovering the high dynamic range image, the resulting image may suffer some blurs due to misalignment. Many algorithms have been proposed to align images and most of them work quite well.
HDR Image recovery: This step attempts to recover the high dynamic image from a set of regular images. There are several algorithms available. One of the very first algorithms was the radiance map algorithm proposed by Debevec and Malik [1].
Tonne mapping: The ranges of typical high dynamic range images usually exceed the display capability of regular computer monitors. That is why we cannot observe the full dynamic range of those images on a computer. Tone mapping is the step that converts the range of a high dynamic range image to the range displayable by regular computers. By doing this, we are able to see the picture on the screen although they do not look as good as they can be.
3. Radiance maps algorithm
3.1. Overall idea
Each camera has a response function which relates the exposure at an pixel to its color. Due to the camera's sensitivity, too low or too high exposures are mapped to the same color. Our target is to recover the exposure that each pixel receives. In order to do that, we need to know the response function. The radiance map algorithm recovers this function as follows.
The exposure X is measured as the product of the irradiance E and the exposure time ∆t. Let Zij be the pixel value of the pixel i in image j, then the response function can be written as:
![]()
It can be rewritten as:

Let
![]() ,
we have
,
we have
![]()
We need to know g(z) for each discrete value of z from Zmin to Zmax where Zmin and Zmax are the minimum and maximum values of a pixel. The problem now becomes minimizing the following objective function. w(z) is a function that reduces the significance of pixels whose values are close to Zmin and Zmax.
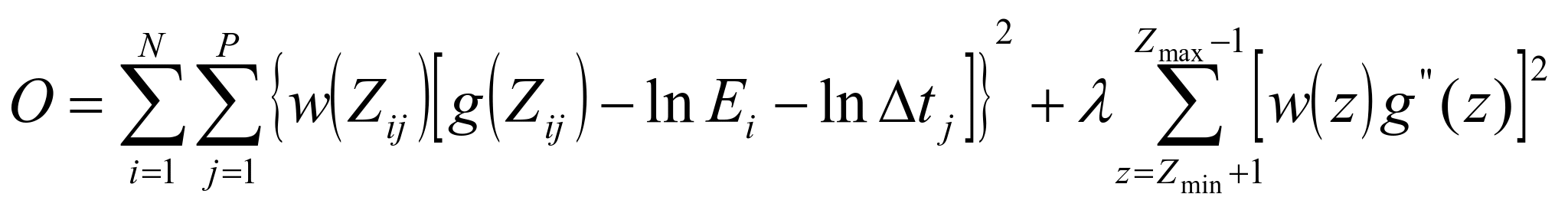
This can be solved by solving the overdetermined system of linear equations using the singular value decomposition (SVD).
After getting values for g(z) for each of z between Zmin and Zmax, we can calculate the irradiance of each pixel as follows:
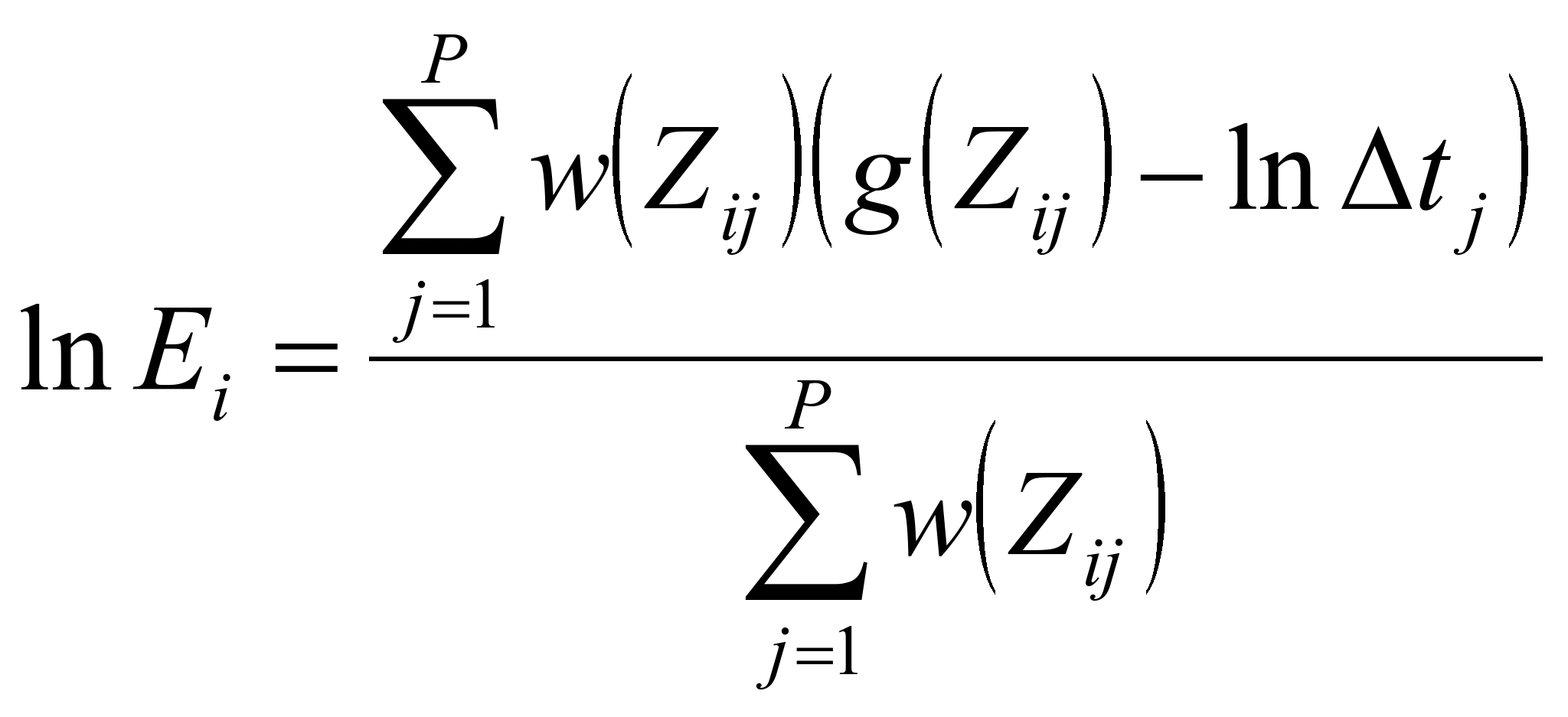
3.2. Implementation
The algorithm is implemented as follows:
We used a collection of 13 images, taken at exposure time from 1/256s to 8s. Each exposure time is a half of the following one. We chose 81 points from these images. To ensure even distribution, we evenly distributed these 81 points across the image.
Each image was then analyzed to get the value for each pixel at each channel.
For each channel, the matrices of the overdetermined system of linear equations were derived. More specifically, the system is in the form A.X=B where:
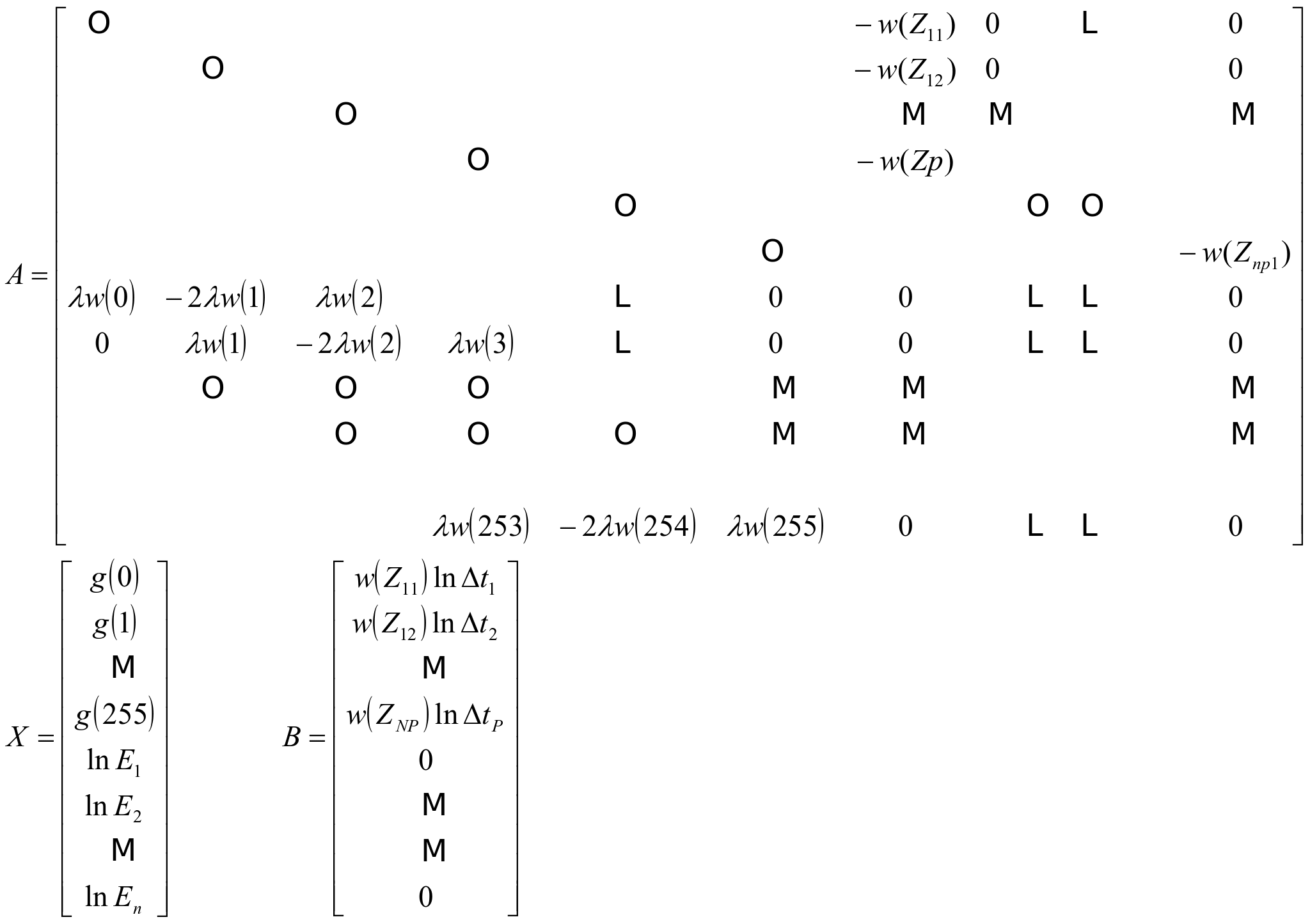
Because the solution to the above equation system can be up to a scale factor, we added the constraint g(Zmid) = 0. In this implementation, Zmid = 128. To add this constraint to the equation system, we simply added one more row into A with value 1 at g(Zmid) and 0 otherwise. The X matrix was still the same and the B matrix was just added one more 0 at the end.
If
we performed SVD on A then
![]() ,
and
,
and
![]() .
.
In our implementation, we used LAPACK++ [3] to perform SVD.
All other matrix operators such as transposing, pseudo inversing, and multiplication were implemented in our program.
The result was written to a high dynamic range (hdr) file. The size of this file is typically about 25MB for an image with the resolution of 3264x2448 (8 Mega Pixels).
3.3. Results
The result we achieved is very optimistic. We were able to recover high dynamic range images. After tone mapping, we can see a very detailed pictures. The recovered response curve for each channel is shown in the following figure. We can see that they are very similar to those presented in the paper by Debevec. That means the algorithm has been implemented correctly.
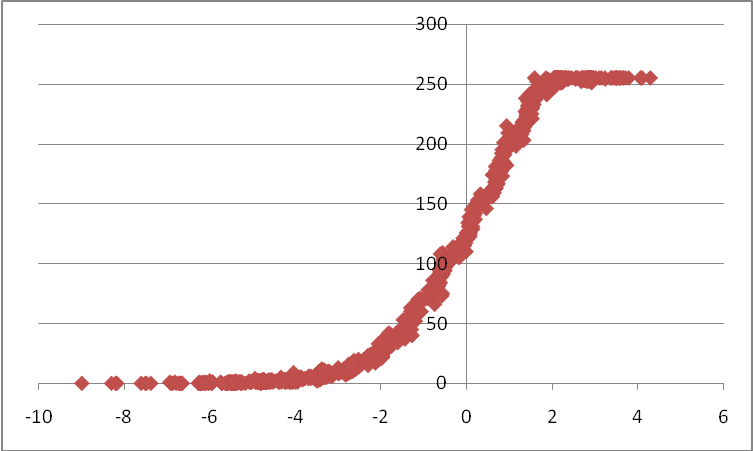
The read channel response curve (Y axis: pixel value, X axis: log of the exposure)
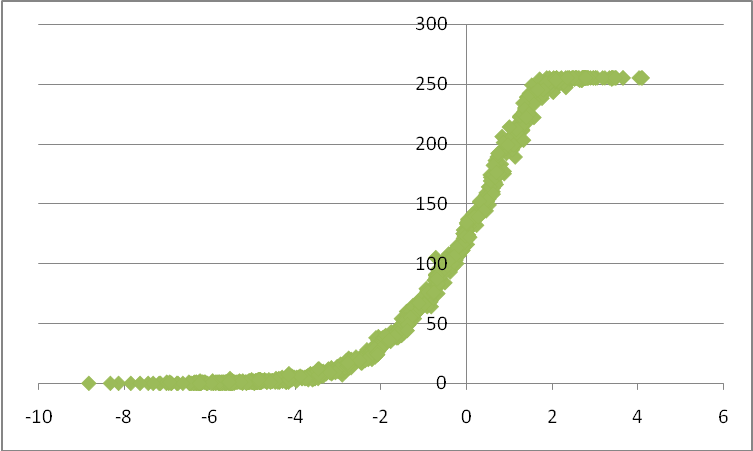
The green channel response curve (Y axis: pixel value, X axis: log of the exposure)

The blue channel response curve (Y axis: pixel value, X axis: log of the exposure)
4. Extension: Median Bitmap Threshold (MBT) algorithm
4.1. Overall idea
Assume we have two images to align. For each image, the algorithm first takes the median value of all the pixels and constructs a median bitmap, in which a value 0 corresponds to a pixel value in the original image that is greater than the threshold and a value 1 otherwise. Basically, if we “and” the two median bitmaps, we will get the difference of the two original images. The smaller this difference is, the better the two images match. As the pixels whose values are close to the thresholds are very sensitive, we do not want to consider them. Thus, an exclusive bitmap is created by setting all the pixel whose values are close to the thresholds to zero and setting to one otherwise. This exclusion bitmap is then “anded” with the median bitmaps to get a better comparison.
To improve the efficiency, a pyramid of images is generated. In this pyramid, the size of each image is halved. The algorithm starts from the top of the pyramid where images have the smallest sizes. It compares the two images at each level of the pyramid and derives the corresponding bit of the distance between two original images. After the two images at the bottom of the pyramid are compared, the algorithm returns the values in X and Y coordinates that the second image needs to shift in order to match the first image.
4.2. Implementation
To simulate the operation of the pyramid mechanism, we developed a recursive function that recursively moves along the pyramid and constructs appropriate bits. There are a number of support functions that we created. For example, we needed to resize images, construct median bitmaps and exclusive bitmaps.
4.3. Results
The result of this algorithm is pretty good. It is able to shift images so that they are aligned with each other. However, a main drawback of this method is the efficiency. Although the pyramid mechanism has been used to speed up the algorithm, it is still very slow, especially with large images. This is because there are many operations need to be done on images in order to compare them.
5. Lessons
The response functions of cameras are very important in images processing. Recovering high dynamic range images is just one application of this response function.
In constructing high dynamic range images, generating the correct matrices for the system of linear equations is very crucial. The parameters must be very accurate; otherwise the recovered images look very bad.
The constraint g(Zmid)=0 is important to balance the three channel values.
Different tone mapping algorithms result in different images.
6. References
[1] Paul E. Debevec, Jitendra Malik, Recovering High Dynamic Range Radiance Maps from Photographs, SIGGRAPH 1997
[2] Greg Ward, Fast Robust Image Registration for Compositing High Dynamic Range Photographs from Hand-Held Exposures, jgt, 2003.
[3] http:// lapackpp.sourceforge.net/