






Step 1: Calibration
Note: the very first thing we did was convert the images to ppm files so Matlab could read them properly.
To do this, for each of the chrome ball images, we computed the centroid of the light spot on the ball, and considered that to be the point of interest. Then we assumed that we were looking in the z-direction, and found the light direction by taking the direction so that the normal was directly between the light direction and the view direction.
In particular, the relevant code for doing this was:
Step 2: Computing surface normals
We converted the image to grayscale, and used these values for the light intensities. Then for each pixel, we solved an over-constrained system (one constraint for each of the 12 images) for the 3 components of the normal. No weighting function was used.
The code for this part was display_rgb_normals.m and solve_normals.m
Step 3: Solving for albedo
The albedo map for each color channel is obtained by simple projection using the normals matrix obtained in the previous step and the lighting matrix from chrome balls.
usage: [r g b]=per_channel_albedo('buddha')
imshow(r);imshow(g);imshow(b)
to see the albedo maps for corresponding set of pictures given as argument to the matlab function.
Step 4: Setting up / solving for surface height
We used the constraints suggested on the project description page, and put these into Matlab's sparse matrix representation. A note on running this: this part takes a few minutes, and the progress bar that is displayed is just for the filling of the matrix elements.
The code for this was get_height_map.m
Extension
EXTENSION:
Estimating surface normals without using the chrome balls
extension_proj3.m.It defines the function extension_proj3. The function takes the name of the directory (eg. Buddha) as its input and returns two images, the surface normal map and the RGB encoded normal map for that particular object.
To run-->
Give the command: [N,M]=extension_proj3('buddha') for example.
It plots the needle map,the RGB encoded map for the object and also finds the normals matrix and the lighting matrix without using chrome ball images.
Algorithm:
Work load
Calibration/Lighting: Blayne/Mayank
Solving for normals: Blayne
Solving for albedos: Mayank
Solving for height map: Blayne
Extension: no chrome balls: Prachi
All Source code files
Running the code :
Usage:
This code depends on things being run with in the directory containing the sub-directory 'psmImages'. It also assumes the images have been converted to ppm (and that extension was added to the file). Let us know if you want such images (they're big, so they weren't submitted).
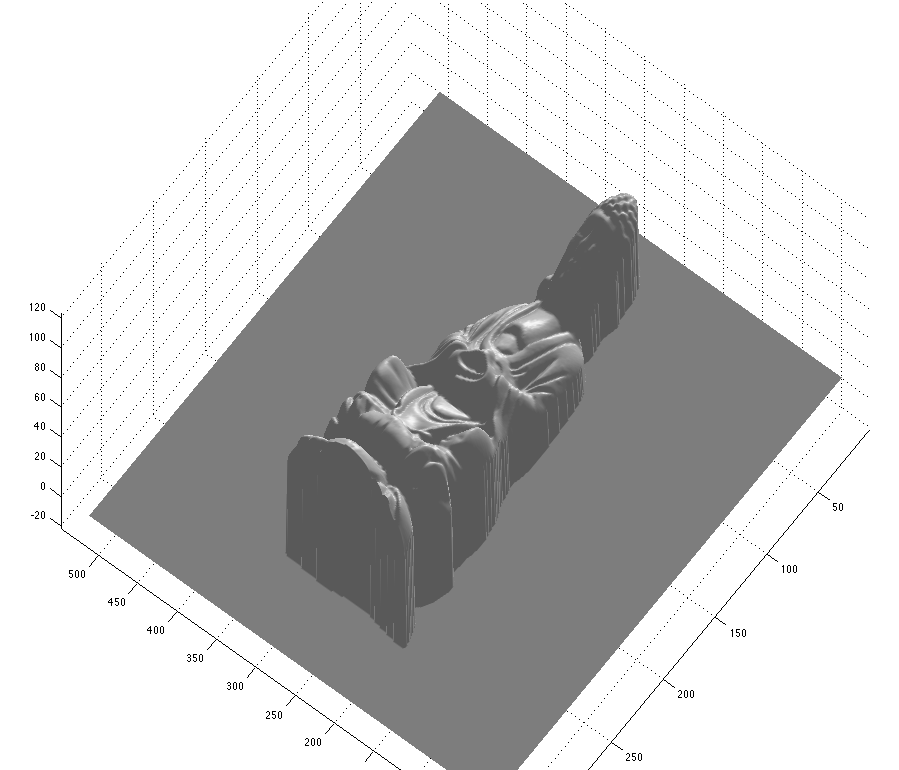
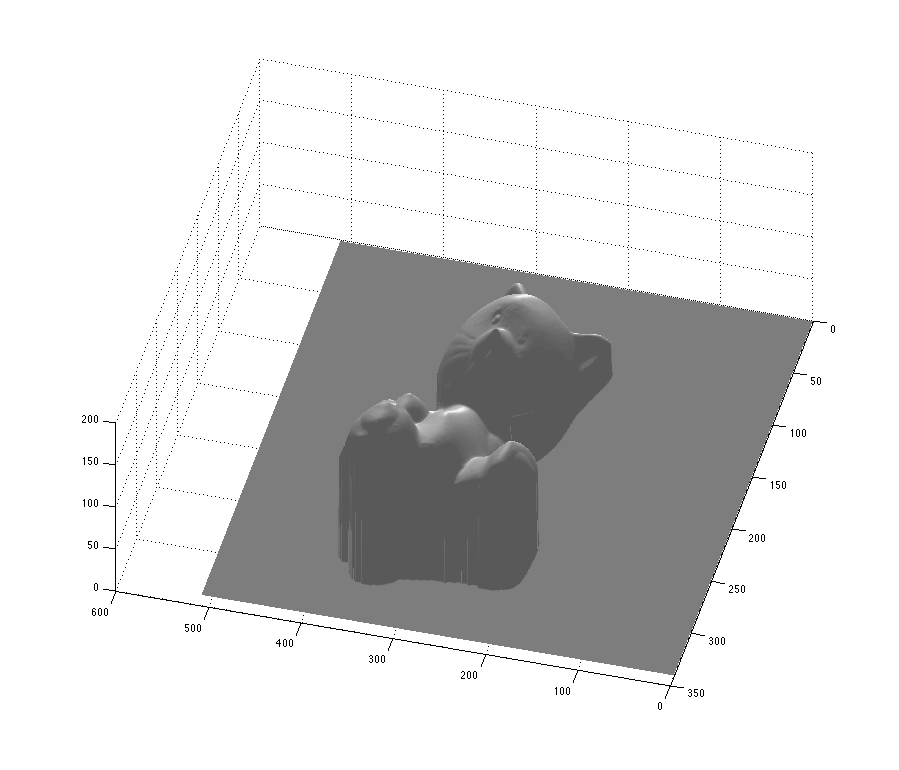
To get the output shown in the gray 3d reconstructions, the commands would be (for the Buddha):
> [l n mask] = display_rgb_normals('buddha');
> h = get_height_map(n, mask);
> surfl(h)
> colormap(gray);
> shading interp
To get the channel albedo map, the commands would be:
> [r g b]=per_channel_albedo('buddha')
> imshow(r);imshow(g);imshow(b)
| Buddha |  |  |  |
| Cat |  |  |  |
| Owl |  |  |  |
| Buddha(R,G,B) |  |  |  |
| Cat(R,G,B) |  |  |  |
| Owl(R,G,B) |  |  |  |
| Horse(R,G,B) |  |  |  |
| Buddha | 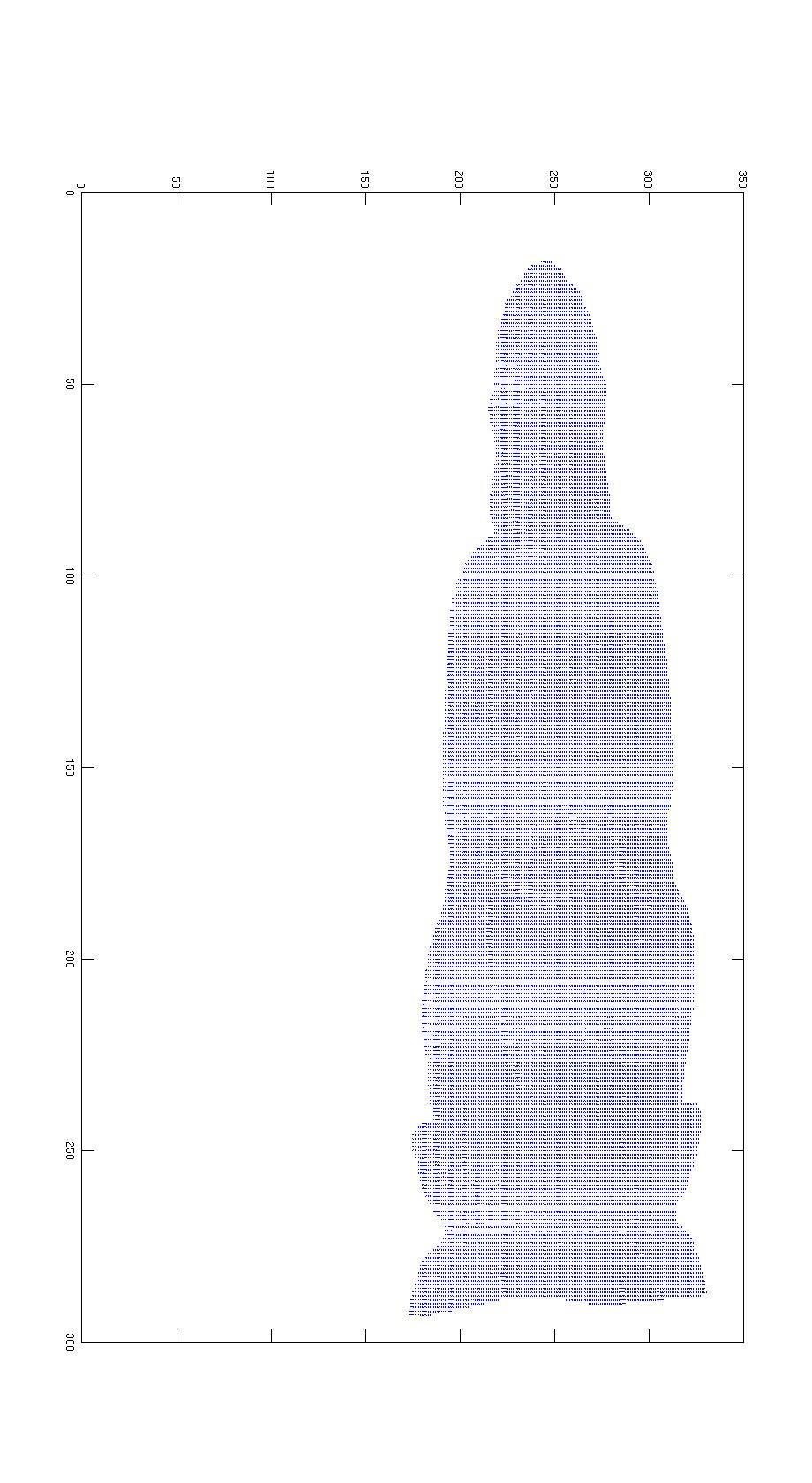 |
| Cat | 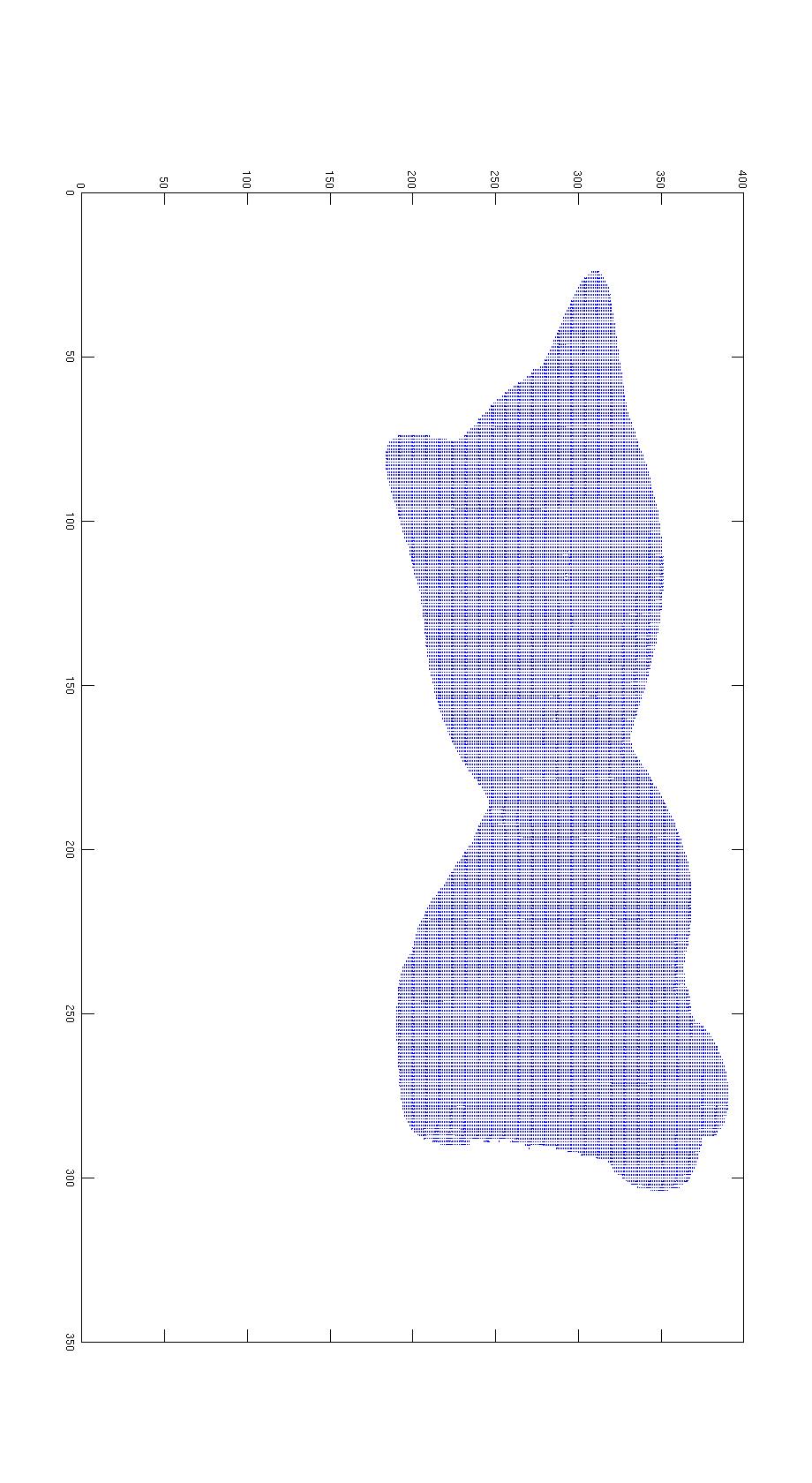 |
| Owl |  |