Project 3 Photometric Stereo

Yi Pan, Mengmeng Chen, Charles Xie

1. Introduction

In this project, we implement a system to construct a height field from a series of images of a diffuse object under different point light sources. We develop software to calibrate the lighting directions, find the best fit normal and albedo at each pixel, and then find a surface which best matches the solved normals.

We read the papers and discussed the algorithms all together.

2. The Approach

2.1 Calibration (done by Yi)

One method of determining the direction of point light sources is to photograph a shiny chrome sphere in the same location as all the other objects. Since we know the shape of this object, we can determine the normal at any given point on its surface, and therefore we can also compute the reflection direction for the brightest spot on the surface.

• Compute the centroid of the ball mask as the center of the ball
• Compute the average distances between the boundary pixels to the center as the radius
• Compute the centroid of the highlight pixels in each lighting image and its distance from the center of the ball, get ( Xp, Yp, sqrt(radius * radius – Xp * Xp –Yp * Yp)), vector N is the normal vector of the ball at point P, equals to OP/R (OP is the vector from the center of the ball to point P)
• Light direction L = 2*(N dp R) * N – R (dp is doc product)

2.2 Normals from Images (done by Yi)

The appearance of diffuse objects can be modeled as where I is the pixel intensity, kd is the albedo, and L is the lighting direction (a unit vector), and n is the unit surface normal. (Since our images are already balanced as described above, we can assume the incoming radiance from each light is 1.) Assuming a single color channel, we can rewrite this as so the unknowns are together. With three or more different image samples under different lighting, we can solve for the product by solving a linear least squares problem. The objective function is:

To help deal with shadows and noise in dark pixels, its helpful to weight the solution by the pixel intensity: in other words, multiply by Ii:

The objective Q is then minimized with respect to g. Once we have the vector g = kd * n, the length of the vector is kd and the normalized direction gives n. I use the same weighting function as we used in project 1. So in the above formula, it is not multiplied by Ii, but intead by weight(i).

2.3 Solving for color albedo (done by Charles)

The objective function is

To minimize it, differentiate with respect to kd, and set to zero:

Writing Ji = Li . n, we can write this more concisely as a ratio of dot products: .This can be done for each channel independently to obtain a per-channel albedo.

2.4 Least square surface fitting (done by Mengmeng)

If the normals are perpendicular to the surface, then they'll be perpendicular to any vector on the surface. We constructed vectors on the surface using the edges that will be formed by neighbouring pixels in the height map. Consider a pixel (i,j) and its neighbour to the right. They will have an edge with direction

(i+1, j, z(i+1,j)) - (i, j, z(i,j)) = (1, 0, z(i+1,j) - z(i,j))

This vector is perpendicular to the normal n, which means its dot product with n will be zero:

(1, 0, z(i+1,j) - z(i,j)) . n = 0

Similarly, in the vertical direction:

We constructed similar constraints for all of the pixels which have neighbours, which gives us roughly twice as many constraints as unknowns (the z values). These can be written as the matrix equation Mz = v. The least squares solution solves the equation

To solve this problem, we used the sparse matrices in Matlab because most of the entries of the matrix are zero.

After computing the surface, use the surfl function to plot out the result of this project.

3. How to Run

In matlab, just simply use phs('image path/imagename_prefix')

4. Experiment Data

We used six different datasets of diffuse objects provided by the project. They can be found under the /psimage directory of our submission.

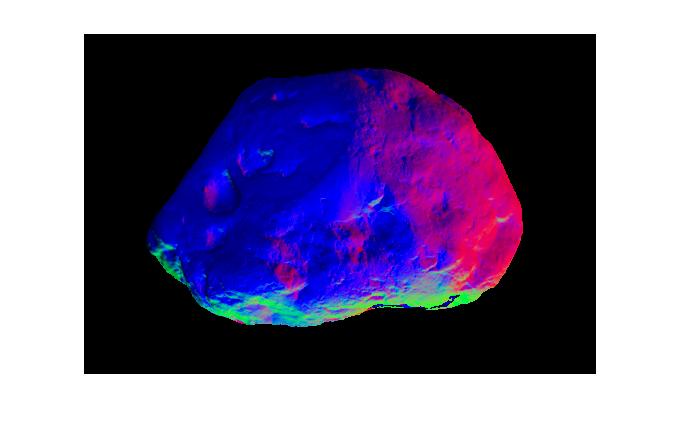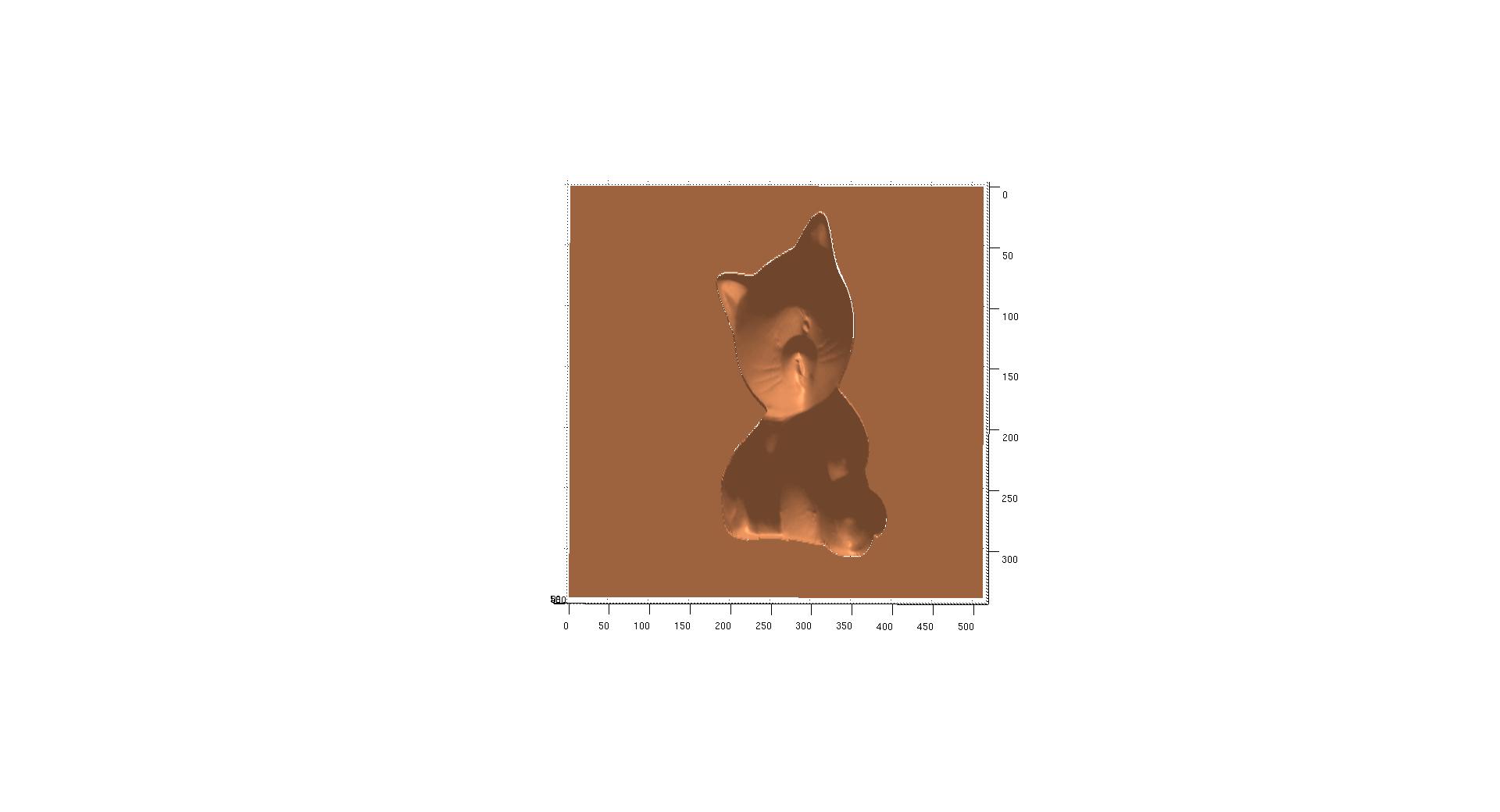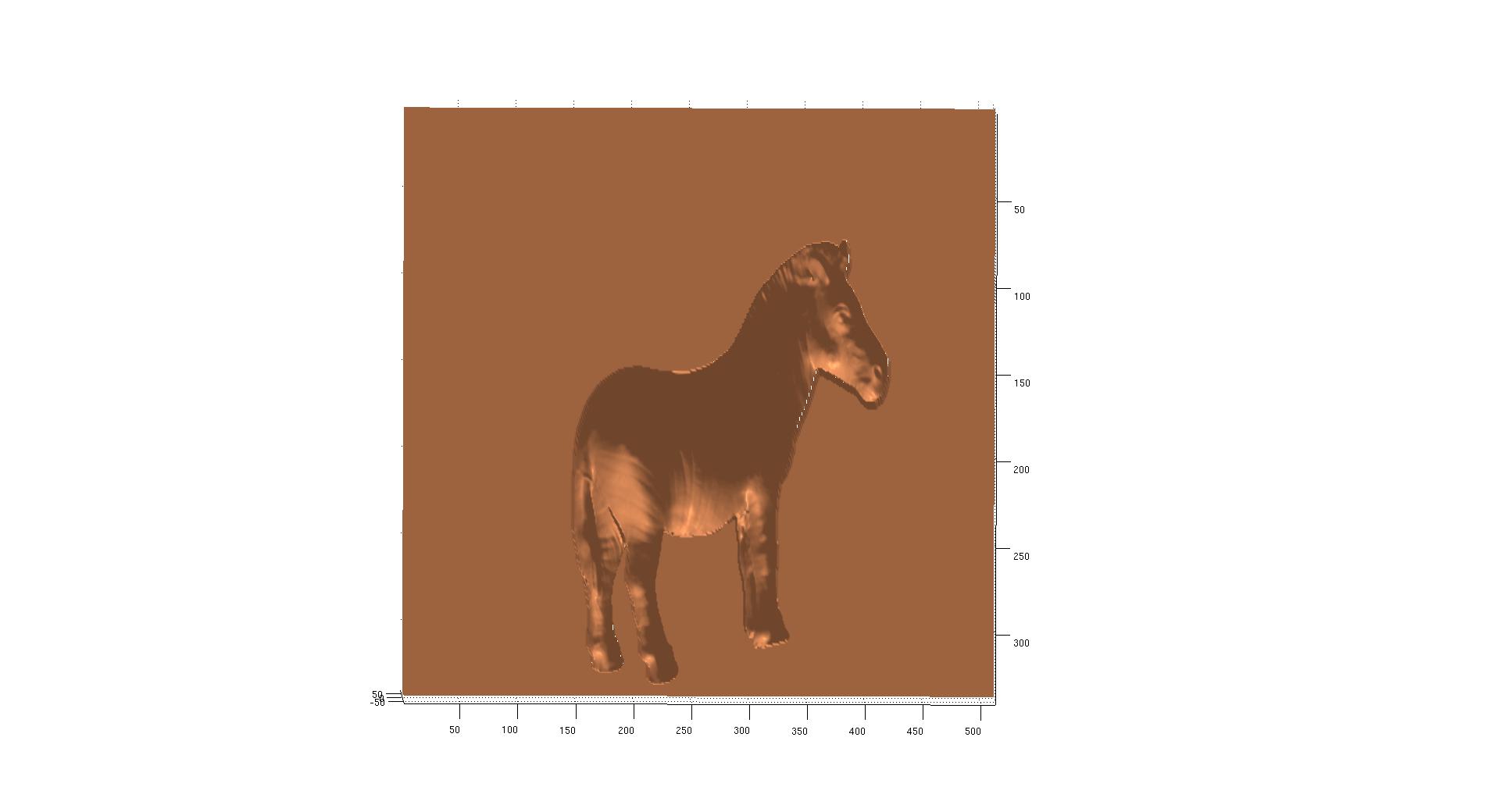5. Results

5.1 Normal maps

5.2 Albedo maps

5.3 3D model views

6. References

1. Woodham, Optical Engineering, 1980, Photometric Stereo.
2. Hayakawa, Journal of the Optical Society of America, 1994, Photometric stereo under a light source with arbitrary motion.
3. Example-Based Photometric Stereo: Shape Reconstruction with General, Varying BRDFs A. Hertzmann, S. M. Seitz. IEEE Trans. PAMI. August 2005. Vol. 27, No. 8, pages 1254-1264.