

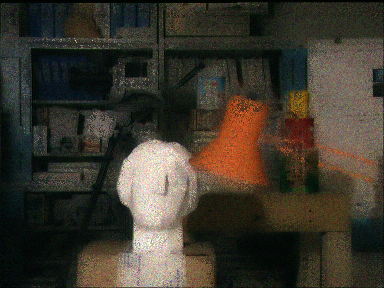
Comparing our method with a state-of-the-art single image denoising [Dabov et al.] and an existing multi-view stereo denoising method [Vaish et al.] on synthetic Poisson noise.
In Matlab, NoisyImage = K*poissrnd(CleanImage/K), where poissrnd is a Poisson random number generator and K=38 for this image set. This operation simulates the process that incoming light is darkened by a factor of K, recorded by a photoreceptor, and then amplified by a factor of K before quatization. At the end, the mean of NoisyImage is CleanImage, and its variance is K*CleanImage.
In the rest of the figures, noisy input images are scaled down by a factor 1/2 to avoid saturating bright noisy pixels for illustration purpose.
Comparison between different denoising approaches
 |
 |
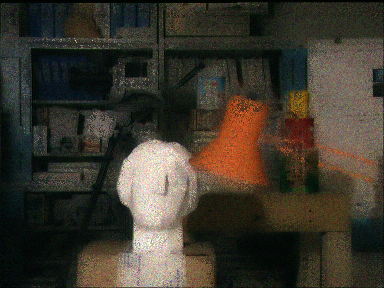 |
One of 25 noisy input images, PSNR=14.1471 |
Single image denoising [Dabov et al.], PSNR=26.476 |
25-view stereo denoising [Vaish et al.], PSNR=19.837 |
 |
 |
Our 25-view denoising (PCA), PSNR: 30.659 |
Ground Truth |
Comparison between different denoising approaches (Insets)
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Noisy Patch |
Single image denoising [Dabov et al.] |
25-view stereo denoising [Vaish et al.] |
Our results |
Ground truth |
Importance of Modeling Signal-Dependent Noise Variance
 |
One of 25 noisy input images |
 |
 |
Single image denoising [Dabov et al.], (with parameter sigma=50) |
Single image denoising [Dabov et al.], (with parameter sigma=98) |
 |
 |
Our result (with parameter sigma=50) |
Our result (with parameter sigma=98) |
 |
 |
Our result (signal-dependent variance) |
Ground truth |
Importance of Modeling Signal-Dependent Noise Variance (Insets)
 |
Noisy Patch |
 |
 |
Single image denoising [Dabov et al.], (with parameter sigma=50) |
Single image denoising [Dabov et al.], (with parameter sigma=98) |
 |
 |
Our result (with parameter sigma=50) |
Our result (with parameter sigma=98) |
 |
 |
Our result (signal-dependent variance) |
Ground truth |
Comment: For both Dabov et al. and our method, using a small and fixed noise variance keeps image details but is unable to reduces large noise over bright regions.Using a large and fixed noise variance reduces noise in all regions but over-smoothes the details in the dark regions. Using signal-dependent variance reduces noise in all regions without loosing details in dark regions.
PCA Denoising versus Tensor Denoising
 |
 |
One of 25 noisy input images |
Our result (PCA) |
 |
 |
Our result (Tensor) |
Ground truth |
PCA Denoising versus Tensor Denoising (Insets)
 |
 |
 |
 |
Noisy Patch |
Our result (PCA) |
Our result (Tensor)
|
Ground Truth |
Comment: PCA and tensor analysis have comparable performance for denoising. Tensor denoising yields smoother results because it tends to treat appearance variation across viewpoints due to occlusion or reflectivity as noise, while PCA is more flexible to preserve these variations.