AVL Trees

• From last time, we know that BST operations take O(h) time where h is the height of the tree. The smallest we could make h was log₂n, where n is number of nodes in the tree.
• Goal: our tree should try to maintain logarithmic height
  • We have to somehow "balance" our trees
• An AVL tree is a binary search tree with an additional balance condition:
  • For any node n in the tree, the height of the left subtree and right subtree differ by at most 1
• Examples:
  
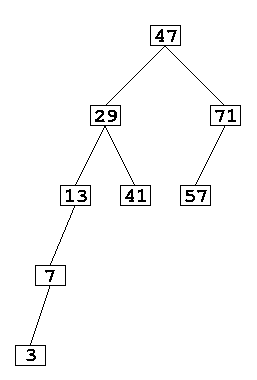
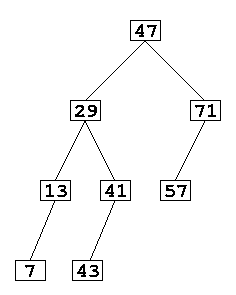
• The first two trees are valid AVL trees. The last 3 are not:
  • The third tree is not balanced at nodes labelled 13, 29, and 41
  • The fourth tree is not balanced at the root: the height along the left branch is 4, while along the right it is 2
  • The fifth tree is not because it is not a BST
• Inserting elements into an AVL tree: begin by inserting like you normally would with an BST
• If the tree becomes unbalanced, have to fix the unbalance
  • Fact: if a tree becomes unbalanced after an insert, only ancestors of the newly inserted node are unbalanced
  • Fact: to fix the balance, we need to concentrate on the deepest node that is unbalanced.
• Call the deepest unbalanced node N. If N was balanced before the insert, there are four possible cases which could cause the tree to become unbalanced:
  1. We inserted the new element into the left sub-tree of the left child of N
  2. We inserted the new element into the right sub-tree of the right child of N
  3. We inserted the new element into the right sub-tree of the left child of N
  4. We inserted the new element into the left sub-tree of the right child of N
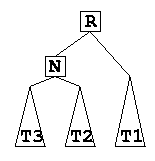
• Resolving situation 1. Suppose before the insert, we had the following situation:
  
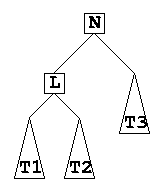
• Note that T1, T2, and T3 are sub trees, with height possibly greater than 1. However: height(T1) = height(T2) = height(T3)
• If we had an element to T1, increasing its height by 1, we have an unbalance at N, resulting in the tree below:
  
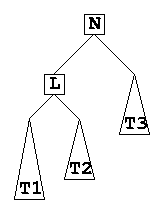
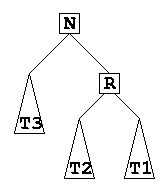
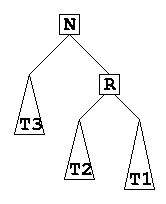
• To fix the unbalance, we shift L up to N's location, make N the root of the L's right subtree. To maintain BST property, we have to make T2 and T3 the left and right subtrees of N, respectively. Finally, we maintain L's left subtree (T1) as is
• This is known as a "single rotation left" and is illustrated below:
  
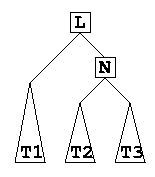
• To resolve situation 2, we perform an analogous single rotation right

  Before insert	After insert	After rotation

• Resolving situation 3: suppose before the insert, we had the following situation:
  
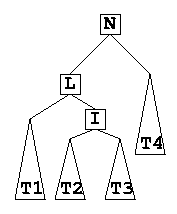
• Note: height(T1) = height(T4); height(T2) = height(T3); height(T1) = height(T2) + 1
• We now add an element to the right sub-tree of the left child of N. That is, we insert an element into either T2 or T3 creating an unbalance. It does not matter which subtree the element was inserted into: the resolution will be the same.
  
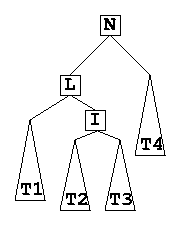
• A single rotation is not good enough
• To fix the unbalance, we have to move I up 2 places. Because L was smaller than I to begin with, we make this the root of I's left subtree. Also, because N was bigger than I to start with, we make N the root of I's right subtree. We then have to place T1, T2, T3, and T4 into the appropriate locations:
  
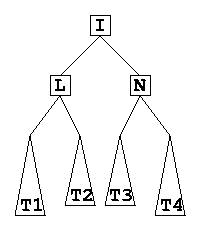
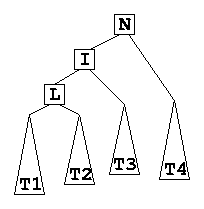
• This is the same as making a single rotation right at L followed by a single rotation left at N:

  After insert	Single Rotation Right	Single Rotation Left

• There is an analogous double rotation for situation 4 (single left rotation followed by a single right rotation)