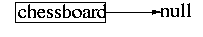
ChessBoard chessboard;
    chessboard = new ChessBoard(8);

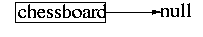
The next statement then creates a new ChessBoard object, and sets the chessboard to refer to (or "point to") the newly created ChessBoard object, as below:

In all honesty, the above picture is not completely accurate: the ChessBoard object actually contains a two dimensional array of char, which is itself an object. That is, there should be a reference coming out of our ChessBoard object (I don't draw that object, however):

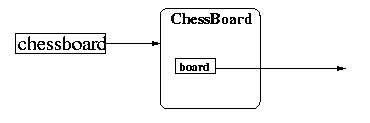
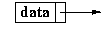
The elements in the list are commonly referred to as a node. The node contains data and a link (reference to) the next node:

Chaining a whole bunch of these together forms our linked list:

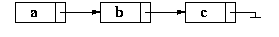
The list contains three items. Therefore, the node which contains a points to the next node in the sequence (b), which points to the final node in the sequence (c). Because there are no items following c, there is no next reference; instead this node's reference will point to null.

We use a ListNode data type to define the nodes in our linked list. A ListNode then must contain to data members: the piece of data the node is keeping track of, and the next ListNode.

In Java, the ListNode class is typically constructed with its data members having package wide access. That is, the data members will only be accessible to other classes within the same package. To specify the package access modifier, we simply declare our members with no access modifier. Therefore, we would likely define the class as follows:

    class ListNode {
        Object data;
        ListNode next;

        public ListNode(Object d, ListNode n) {
	    data = d;
	    next = n;
        }
    }

We need to define the operations we will be able to use on a data structure. We have the four basic methods we want to be able to perform on any structure: add, remove, get, and contains:

add(x)
Input: the element to be added to our list
Postcondition: the element has been added to the front of the list

remove(x)
Input: the item to be removed front the list
Returns: true if the list contains x, false otherwise
Postcondition: Removes the first occurrence of x from the list

get()
Returns: the item at the front of the list

contains(x)
Input: the item sought in the list
Returns: true if the list contains the item, false otherwise

Our LinkedList data structure will contain one data member: a "header" node which will contain a link to the front of the list. It is important to note that this header note is not actually part of the list, but is a ListNode which contains no data (that is header.data = nulland whose next points to the ListNode which is the front of the list. If there are no items in the list, next will point to null.

When adding a new item to the list, there are many steps that must be performed:

1. The new list node must be created
2. The data must be inserted into the new node
3. The next pointer must be correctly set
4. Header's next pointer should be set to the new node

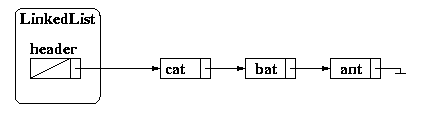
If we want to add dog, we must first create a new node:

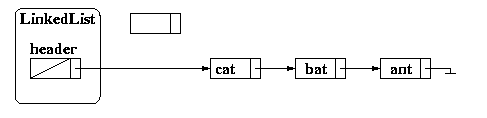
then add dog to the node,

then set the next pointer for this new node,

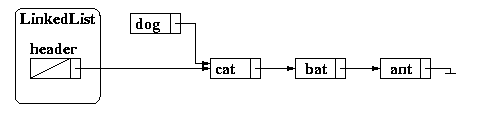
and then finally update our header node:

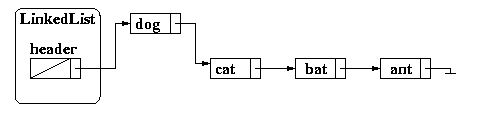
This process is formalized below:

add(x)
Input: the element to be added to our list
Postcondition: the element has been added to the front of the list

    Create a new ListNode, tmp
    tmp.data = x
    tmp.next = header.next
    header.next = tmp

The use of a header node is a long standing debate amongst Computer Scientists: some claim that it is useless to have a header node because it contains no information. Instead it should only be necessary to have a node denoted as the front of the list, which is set to null when the list is empty. Instead, we use a header node to avoid the check of a special case (head ==- null) of inserting into an empty list.

If we were to implement the add method in Java, we could combine the four steps into one:

    header.next = new ListNode(x, header.next);

get()
Returns: the item at the front of the list

    if header.next == null
        error: underflow
    return header.next.data

To see if our list contains a specific item, we must examine all of the elements in the list, one element at a time. Thus, we start at the first item after the header (header.next) and look at that element and then all subsequent things in the list until we either find the element, or run out of things to look at:

contains(x)
Input: the item sought in the list
Returns: true if the list contains the item, false otherwise

    tmp = header.next
    while tmp != null
        if tmp.data == x
            return true
        tmp = tmp.next
    return false

Before we get to the pseudocode for our remove method, let us discuss what is supposed to happen. Consider again, our linked list of dog, cat, bat, and ant.

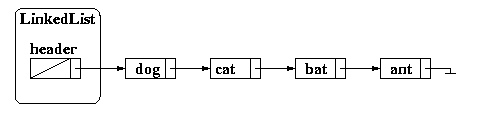
To remove bat from the list, we actually have to change the next pointer for the node prior to bat. That is, we must change the list to look like the following:

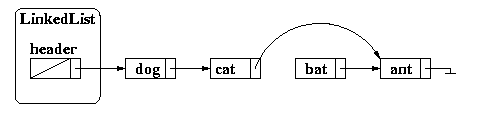
The node which contains bat will then be garbage collected because there is no longer anything pointing to it.

To perform our removal, we perform steps similar to what we did for contains: we have to look at each element in the list until we find the element to be removed. This time, however, we must also be keeping track of the node prior to the node to be deleted. However, instead of keeping track of two references, we simply use one and just look ahead to the correct node:

remove(x)
Input: the item to be removed from the list
Returns: true if the list contains x, false otherwise
Postcondition: Removes the first occurrence of x from the list

    tmp = header
    while tmp.next != null
        if tmp.next.data == x
            tmp.next = tmp.next.next
            return true
        tmp = tmp.next
    return false

On the other hand, to search and remove from our list, we have to look at all of the elements in our list, one element at a time. If there are n elements in our list, therefore, it will take O(n) time to perform these actions.

Notice how our implementation of a linked list is very similar to a stack: we perform all additions and accesses at the front of the list. Indeed, if we changed remove such that the first element is always the one removed, we will have a stack:

removeFront()
Input: the item to be removed from the list
Returns: the item at the front of the linked list Postcondition: Removes the first item from the linked list

    if header.next == null
        error: underflow
    tmp = header.next.data
    header.next = header.next.next
    return tmp

The advantage of this implementation of a stack is that it avoids all of the copying that had to be done whenever we expanded the size of the array. With the linked list, there is no limit to the number of items we can store in the structure.

It is also possible to use a linked list to implement a queue. We just need to add a tail reference, which always refers to the last item in the linked list. Then, all additions will go at the tail of the list, and all removals will be done at the front. When there are no items in the list, tail should be equal to the header. I show the updated add method below:

add(x)
Input: the element to be added to our list
Postcondition: the element has been added to the end of the list

     tail.next = new ListNode(x, null);

We can use the definition of removeFront for removing from our list. We must be sure, however to add a special case for removing the last item from the list:

removeFront()
Input: the item to be removed from the list
Returns: the item at the front of the linked list Postcondition: Removes the first item from the linked list

    if header.next == null
        error: underflow
    tmp = header.next.data
    if header.next == tail
        tail = header
    header.next = header.next.next
    return tmp

addBefore(x)
Input: the item to insert into this list
Postcondition: x has been added to the list prior to the current position; the new node is considered to be current

addAfter(x)
Input: the item to insert into this list
Postcondition: x has been added to the list after the current position; the new node is considered to be current

advance()
Postcondition: current has been advanced one spot

advanceTo(x)
Input: the item being sought, x
Returns: true if the item is in the list, false otherwise
Postcondition: current has been updated to point to the first occurrence of x get()
Returns: the data item at the current location

remove()
Returns: the current item in the list
Postcondition: the list no longer contains the current item; current has been update to the item following the removed item

rewind()
Postcondition: current is set to be the first item in the list

We need more than just a header node to keep track of our list: we also need a current node. And since we will be performing deletions at this current node, we also need to keep track of the node prior to the current node. When the list is empty, we will define current to be null. Finally, we need to worry about the boundary conditions of our iterator: for instance, what happens if we are at the last position of the list, and we advance? Or, similarly, we remove the last item in the list. What should we do in this case. It is possible to answer these questions in several ways. We attempt to reconcile these problems by adding one more method to our interface:

inList()
Returns: true if current is at a valid location in the list, false otherwise

That is, we allow ourselves to make a call to advance off of the end of the list. If this happens, we can not allow all of our other actions (our adds, removes, and gets) to happen. We are not in the list if current == null.

We need one other method of this type: a method which checks if the list is empty. The list is empty is header.next == null.

We implement our methods below:

inList()
Returns: true if current is at a valid location in the list, false otherwise

    return current != null

isEmpty()
Returns: true if the list is empty, false otherwise

    return header.next == null

addBefore(x)
Input: the item to insert into this list
Postcondition: x has been added to the list prior to the current position; the new node is considered to be current

    if isEmpty()
        header.next = new ListNode(x, null)
        current = header.next
        return
    else if !inList()
        error: index out of bounds
    tmp = new ListNode(x, current)
    prior.next = tmp
    current = tmp

We define a method to add after the current node in a similar way:

addAfter(x)
Input: the item to insert into this list
Postcondition: x has been added to the list after the current position; the new node is considered to be current

    if isEmpty()
        header.next = new ListNode(x, null)
        current = header.next
        return
    else if !inList()
        error: index out of bounds
    tmp = new ListNode(x, current.next)
    prior = current
    current.next = tmp
    current = tmp

advance()
Postcondition: current has been advanced one spot

    if isEmpty()
         error: underflow
    if !inList()
         error: index out of bounds
    prior = current
    current = current.next

    tmp = header
    while tmp.next != null
        if tmp.next.data == x
            prior = tmp
	    current = tmp.next
	    return true
        tmp = tmp.next
    return false

    if isEmpty()
        error: underflow
    if !inList()
        error: index out of bounds
    return current.data

    if isEmpty()
        error: underflow
    if !inList()
        error: index out of bounds
    prior.next = current.next
    current = current.next

    current = header.next

Instead of having the notion of being "outside of the list" when we advance too far in our list iterator, many people find it useful to use the idea of a "circular linked list". We were introduced to this circular idea when we first discussed queues: the notion of when we get to the end of a data structure, we should wrap back around to the beginning. This can be accomplished quite easily with our linked list: instead of having the last item point to null, we could simply have it point back to the beginning of the list:

We would have to be careful in our code for advanceTo and contains to avoid going around the list forever if our item is not in the list. This could easily be avoided by maintaining the number of elements in the list.

A circular linked list with only one element is a fairly strange picture: the next pointer will actually point to itself!

Doubly linked lists

You may have noticed that with linked list iterators, it is only possible to move forwards in the list. It would be nice to be able to move backwards as well. At first glance, it should appear that this should not be too difficult: we have a prior node, if we want to go back, just set current to the prior node. The problem is that we will then have no way to update prior.

This whole situation can be rectified by changing our list slightly, such that each node keeps track of the node before it as well as the node after it:

To add a node to such a list, we have to many more things to update than we did in a singly-linked list:

1. Create a new list node
2. Add the data to the node
3. Add the prior pointer
4. Add the next pointer
5. Update the prior node's next pointer
6. Update the next node's prior pointer

Of course, it is also possible to make our doubly-linked list a circular doubly-linked list.