Trees

Day 1, Day 2

Introduction

So far, all data structures have been "linear": items follow one after another
Next comes trees: number of items following another item may vary
Advantages: Insert/delete are fast; find is fast (usually)

Tree Basics

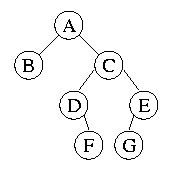
What is a tree? Consider the following example:

Terms
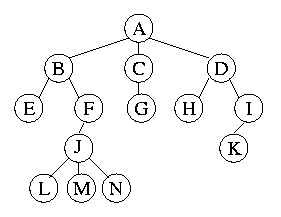
- Node: data (the value we actually care about) and key (the value used to find the data), plus branches to other nodes. All of the above circles are considered to be nodes of the tree
- Edges: The "branches" mentioned above. An edge is each line drawn in the image. The branches are usually considered to be directional: if you have an edge from A to D, you are not allowed to follow the edge back from D to A.
- Each branch leads to a child. B - N are all children of some kind.
- All of the fellow children are known as siblings. B, C, and D are all siblings.
- All siblings have a common parent. However, a child is usually not aware of its parent: instead, parents keep track of only their parents. B, C, and D all have the common parent, A. A node is only allowed to have one parent.
- There is a special node which has no parent: the root. Above, A is the root node.
- The number of children a node has is the the degree. A and J are of degree 3; K is of degree 0: it has no children.
- Some nodes have no children: these are known as leafs. E, G, K, L, M, and N are all leafs.
- An interior node is a non-leaf node. An interior node always has at least one child. A, B, D, F, and I are all interior nodes.
- The depth of a node is the number of edges which must be taken in traversing from the root to that node. For instance, the depth of K is 3. The root has depth of 0.
- The height of a node is the maximum length of a reachable path from this node to any other node. Note, that we are only allowed to travel down the tree: the parent is not included as being a reachable node from a given node. We can make a recursive definition of the height of a node: The height of a leaf is 0. The height of an interior node is 1 + the maximum height of any child. The height of D is 2; the height of M is 0. The height of the tree is the height of the root: 4 in the tree above.
- Size of a node is the number of descendants of a node; including the node itself. The size of D is 4; K is 1; and A is 14.
- Subtree: we can view each node as the root of a separate tree. Indeed, trees are often defined recursively. B, C, and D are the roots of subtrees of A
- A tree with no data is said to be empty

Representing Trees

Option 1: An array of references
We could use an array of references to store all of the children. A problem is that we may have to assume a specific size. Or, we could use a Vector for the children

Option 2: Linked List Representation
Each node has a reference to its first child as well as to its next sibling.

Binary Trees

binary tree

An important kind of binary tree is a full binary tree. In a full binary tree, all of the children (except the leafs) degree 2, and all leaves are at the same level.

Also, a complete binary tree is like a full tree, except the bottom level may not be totally filled in. However, all leafs are filled in from left to right.

Traversals

A traversal is looking at all of the elements in your structure, no matter what that structure may be.
They are useful for finding elements (if your data is unordered), printing, or inserting and deleting.
Linked list traversals were pretty easy, because it was easy to go to the "next" element
Trees are more difficult: there is more than one next
Traversing a general tree: possible but not discussed
Instead, we concentrate on traversing binary trees.

Binary Tree Structure

Recall, trees are made up of nodes. Therefore, a binary tree is made up of a binary tree node. The tree actually only keeps track of one node, the root. All other nodes are kept track of the root by following the left and right branches of the root. A binary tree node contains a piece of data (typically, of type Object in Java), and two other BinaryTreeNodes for the left and right.

Recursive Binary Tree Traversals

There are several things we have to do in recursively traversing a binary tree:
1. visit the root
2. visit the left subtree
3. visit the right subtree
The way we order the top three produces different ordering.
There are 3! = 6 different ways to order the above
Convention: always visit left subtree before right subtree: 3 possibilities

The tree used:

Preorder:

visit root
visit left subtree
visit right subtree

Pseudocode:

    Preorder(BinaryTreeNode node)
        if (node == null)
            return
        print node.data
        Preorder(node.left)
        Preorder(node.right)

Preorder printing of above tree gives: A, B, C, D, F, E, G

Inorder:

visit left subtree
visit root
visit right subtree

Pseudocode:

    Inorder(BinaryTreeNode node)
        if (node == null)
            return
        Inorder(node.left)
        print node.data
        Inorder(node.right)

In order printing of above tree gives: B, A, D, F, C, G, E

Postorder:

visit left subtree
visit right subtree
visit root

Pseudocode:

    Postorder(BinaryTreeNode node)
        if (node == null)
            return
        Postorder(node.left)
        Postorder(node.right)
        print node.data

Postorder traversal of above tree gives: B, F, D, G, E, C, A

Level Order Traversal

Goal: Print all siblings before moving on to children

Pseudocode:

    Levelorder(BinaryTreeNode root) 
        enqueue root into Q
        while Q is not empty
            node = dequeue from Q
            print node.data
            if node.left != null
                enqueue node.left into Q
            if node.right != null
                enqueue node.right into Q

Level order traversal of above tree: A, B, C, D, E, F, G