
Statisticians are known for juggling numbers, but there's a lot more to it than you might think. Let's see how to juggle the most famous number of all.
The story can be told with any number of balls, but we start with 3 since it's the most popular juggling number. Instead of writing π as we usually do in base 10 (i.e. 3.1415926535897932384…), let's imagine that we have fewer symbols at our disposal, say 3, and we'll write it in that base:
Recall, because you only have symbols 0, 1, and 2, you have to double up to get three, giving 10 to the left of the decimal point. The basic juggling plan is pretty simple. Associate each ball with a digit; imagine that as time goes along (left to right) you throw the ball (digit) corresponding to where you are in the expansion. That ball lands again at some later point, exactly when it occurs next in the expansion. After each throw you look one place to the right and make the next required throw. The throws will need to be of varying heights in order to make up for the irregular sequence of digits in the expansion; the greater the number of steps to the next occurrence of the thrown digit, the higher the throw. For convenience we'll associate the actual heights (whose values would depend on the physics of the situation) with the numbers of required steps in the expansion. Relative to the base 3 that we're working in:
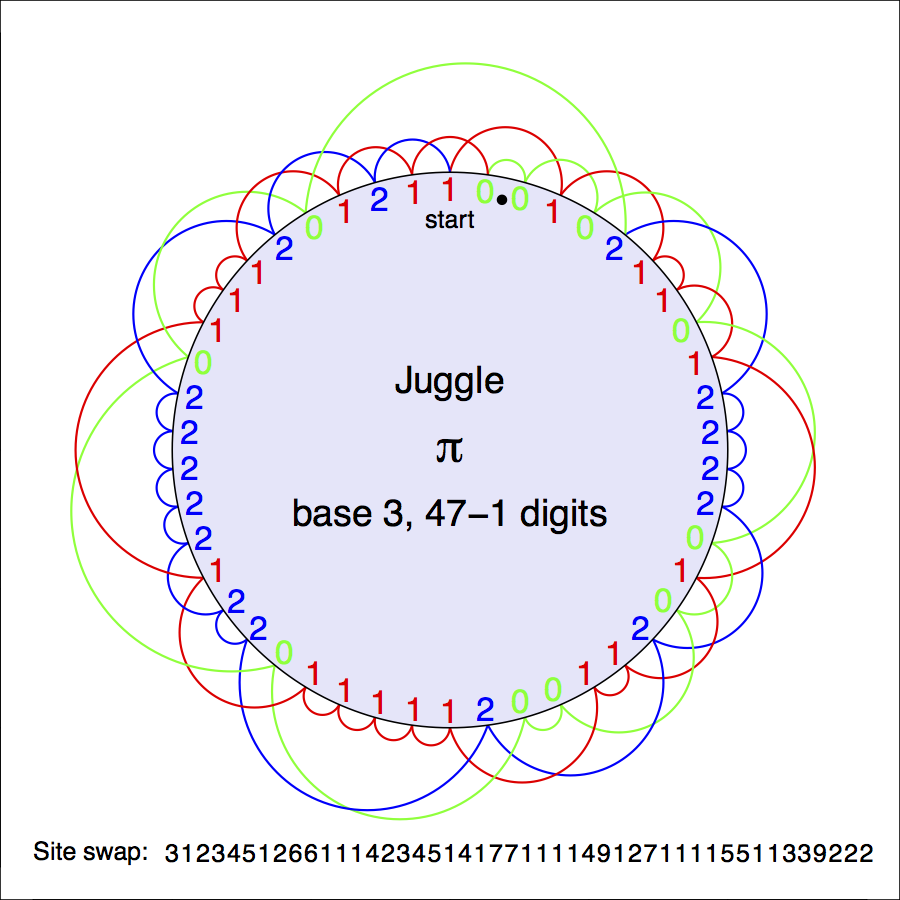
A juggler (surely a very talented one) can proceed happily throwing balls following this transformed base-3 expansion. No big deal, except that if you want a finite approximation (so that you or maybe a machine might ever hope to learn how to juggle part of π) you need to be a bit careful with how you stop. Jugglers have for a long time known how to describe juggling patterns with a compact number sequence called site swap. Roughly speaking, a site swap is a sequence of throw heights. But not just any sequence of throw heights will do, since the constructed juggling pattern is considered to be cyclical and, in principle, could be repeated indefinitely. To make a site swap pattern from a finite chunk of π, we have to truncate the height sequence at a legal spot. The figure below might help to explain. We wrap a finite chunk of the expansion around a circle, starting at 12:00 noon, say, and indicate the throw heights by curves, as shown. A legal truncation point is one where all the throws generated towards the end of the finite expansion (late morning) land again nicely after the beginning (early afternoon), with no collisions and no gaps. It so happens that a legal site swap for base-3 π occurs in 46 digits (obviously a significant number, since it's one shy of the Madison Area Jugglers' most significant number!) Indeed, stick man above is doing a most impressive run of this pattern. Note that stick man has two hands and is juggling in a standard way right-left-right and so on. This means that even throws go to the same hand (two's are holds) and odd throws go to the opposite hand. Most mortals will find this pattern very hard, both to commit to memory and to juggle. It happens that the first 9 digits also works: 312345126. Give it a try!

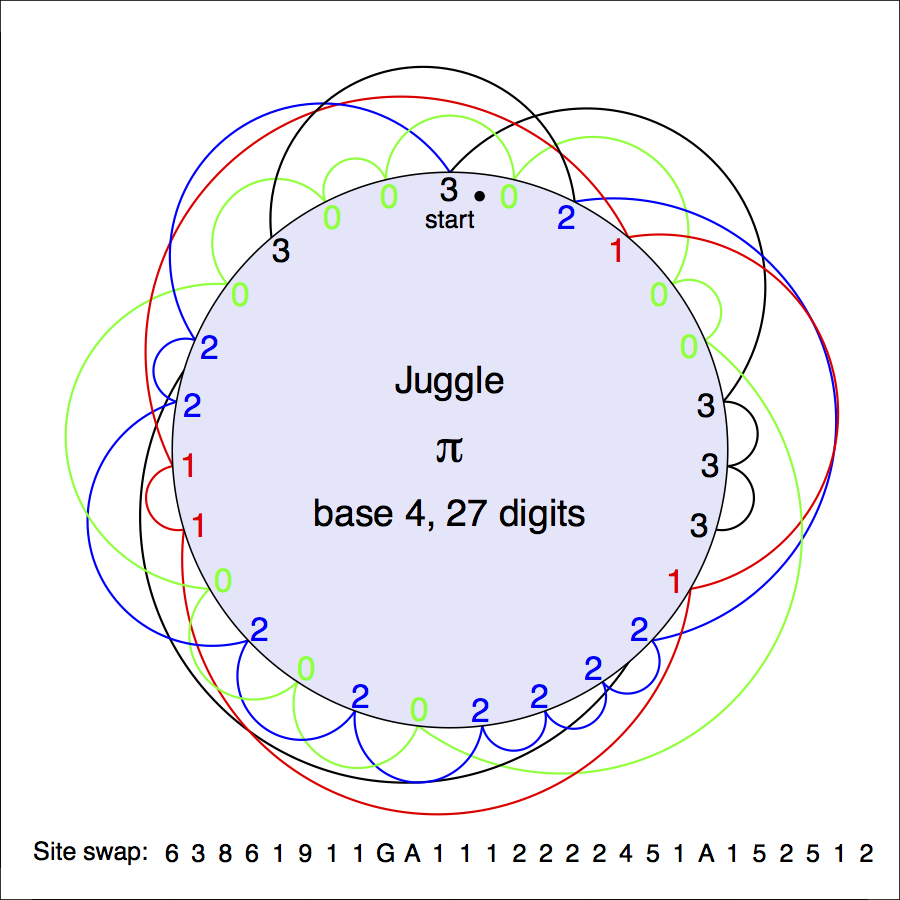
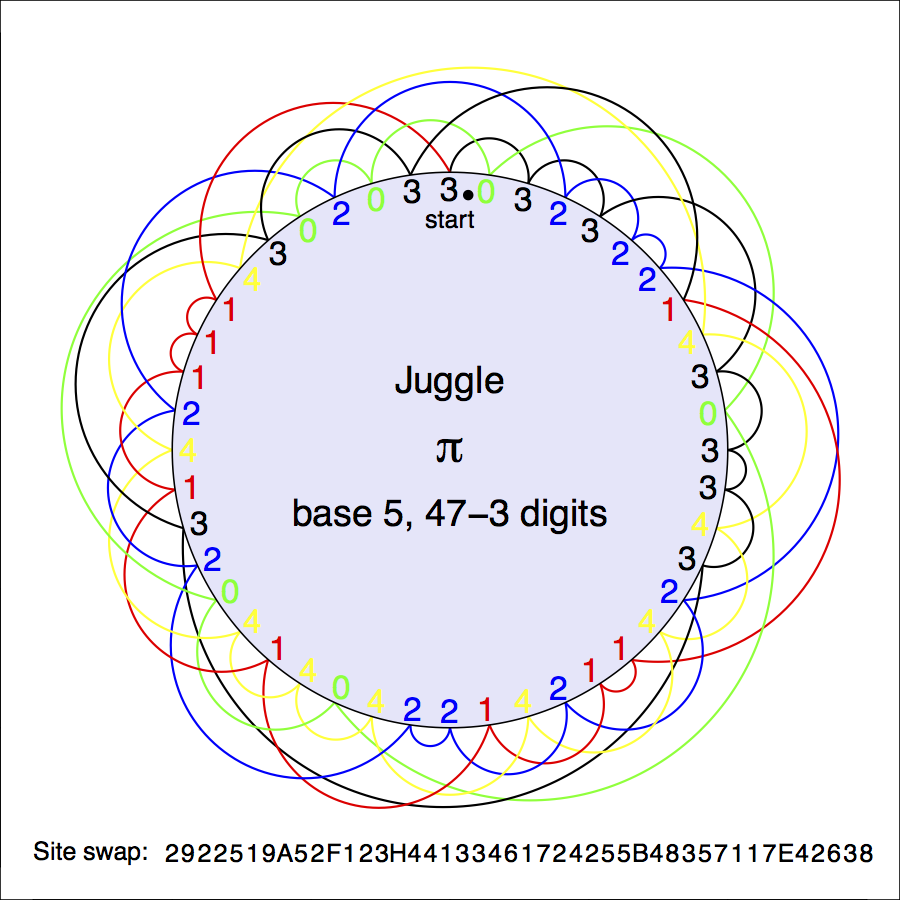
There's nothing stopping us from working out juggling patterns for more balls. The two figures below show site swaps for 4 and 5 balls. Notice that they start with expansions of π in the same base as the number of balls being juggled. Good luck trying them; there are some awfully big throws. Remember the convention in site swap, letters are used to get into the two-digit throws.
Technically, the three-ball juggler (stick man above) is not juggling the first 46 digits of π but rather the first 46 throw heights derived from the expansion of π. We need to know a few more digits in the original sequence to make sure our site swap is valid.
