$ tar -xzf scrm2.v2.2.tar.gz
make the executable in the program directory by changing directory and typing "make"
$ cd scrm2.v2.2 $ make g++ -Wall -O3 -static -c scrm2.cpp g++ -Wall -O3 -static -c Option.cpp g++ -Wall -O3 -static -c grid.cpp g++ -Wall -O3 -static -c genomic.cpp g++ -Wall -O3 -static -c fasta.cpp g++ -Wall -O3 -static -c Timer.cpp g++ -Wall -O3 -static -c CRM.cpp g++ -Wall -O3 -static -c Distance.cpp g++ -Wall -O3 -static -c IOExample.cpp g++ -Wall -O3 -static -c metric.cpp g++ -Wall -O3 -static -c io.cpp g++ -Wall -O3 -static -c custom.cpp g++ -Wall -O3 -static -o scrm2 scrm2.o Option.o genomic.o grid.o fasta.o Timer.o CRM.o Distance.o IOExample.o metric.o io.o custom.o g++ -Wall -O3 -static -o fasta2markov fasta2markov.cpp fasta.o Option.o Timer.o genomic.o grid.o g++ -Wall -O3 -static -o pwm2fasta pwm2fasta.cpp Option.o g++ -Wall -O3 -static -o revcomp revcomp.cpp Option.o genomic.o fasta.o $
Run the binary, "scrm2" created by the installation process above.
Basic usage is: scrm2 [options] postive-FASTA-file negative-FASTA-file.
The input to the program is a set of two files containing sequence data: A set of positive example sequences and a set of negative example sequences. These are in FASTA format:
Basic usage is: scrm2 [options] postive-FASTA-file negative-FASTA-file.
Options are associated with a keyword and often a single letter. Keywords are preceeded with two dashes, single letters with one. For instance, the PRNG seed is set with --seed 12345 or -S 12345 (one could also use --seed=12345, -S=12345, or -S12345).
For help, run scrm2 --help. This will list all the options, their keywords, default values, and give a brief description.
There are many options. What follows is a list of the ones you'll want to consider.
| Option Keyword(s) | Meaning | Comments |
|---|---|---|
| -C, --C | Max. binding sites | Usually set to --C=3. That means the final solution will have one, two, or three binding sites, but the program will never consider four. |
| -D, --D | Max. motifs per binding site | Each binding site may have multiple motifs. If any are present, the binding site occurs in the sequence. This can represent variability in a binding site motif, but each motif is learned separately. This is optional, and sometimes people prefer to set --D=1 and have each binding site represented by a single motif. |
| -G, --G | Max. negated binding sites | Set --G=0 if you don't want to consider negated motifs. |
| -Z, --timeout | Max. number of considered models | The algorithm will stop after considering a total of this many model structures. This includes learning single-motif models, possibly based on candidate motifs. |
| -m, --mm | Variable-order Markov chain background distribution file | The algorithm will work better with a good model of the background distribution (promoter DNA). It uses a Markov-chain model for this (same as MEME). One can be created from FASTA sequence data using the fasta2markov program. |
| -b, --bg | Background distribution file |
Arbitrary background distribution per sequence. FASTA-like format:
Following i numbers are the LOG-SCALE likelihood of the subsequence
up to, but not including position i (so there are L+1 numbers
for a sequence of length L). Example:
|
The following are options you may or may not want to consider.
| Option Keyword(s) | Meaning | Comments |
|---|---|---|
| -N, --folds | cross-fold validation folds | To run 10-fold cross-validation, set this to 10, and set the -F, --fold option appropriately. |
| -F, --fold | Which fold? | For N-fold cross-validation, run N times, setting -F=0, -F=1, ..., -F=N-1. This is (stratefied) N-fold cross-validation. The algorithm will set aside every Nth positive and negative example sequence for testing. Specifically, if all P positive examples are numbered 0 through P-1, and all G negative examples are numbered P through P+G-1, then an example numbered i is held aside for testing if i modulo N = F. |
| -w, --minw | Minimum motif width | The algorithm will try various CRM model structures by adding new motifs to promising learned models. When it adds a new motif, it is randomly initialized and given a random width at least this many base pairs. |
| -x, --maxw | Maximum motif width | Self-explanatory, see -w, --minw above. |
| -W, --weights | Sequence weights input file | If you are more confident about some sequences than others,
you can assign a weight (between zero and one) to each sequence. This
is interpreted as the probability that it contains the CRM.
The input file looks like FASTA, but just contains each sequence's weight.
For instance:
Input FASTA file: > Sequence0 ACTACTACAATCGACTAGCATCGATCACTAACAGCATCA... > Sequence1 ACTGACTATTTACGACGATCAGCATAGCATACGACAACA... ... Weights file: > Sequence0 1.0 > Sequence1 0.80 ... |
| -V, --prior | Binding site location prior input file | If you have an idea of where on each sequence binding is more likely to
occur (say, via comparative genomics), you can indicate this with a number
for each sequence, for each location (individual base), indicating the relative
probability of the binding site occuring there.
For instance:
Input FASTA file: > Sequence0 ACTACTACAATCGACTAGCATCGATCACTAACAGCATCA... > Sequence1 ACTGACTATTTACGACGATCAGCATAGCATACGACAACA... ... Prior file: > Sequence0 0.0023 0.0123 0.0199 ... > Sequence1 0.0001 0.0022 0.0037 ... ...There are as many numbers for each sequence as base pairs for that sequence. |
| -r, --ratio1 | Search ratio (|m|=1) | To speed up convergence, the algorithm may consider only the most likely positions for each binding site. For instance, given a motif, it may be 99% probable that if the motif occurs, it occurs in one of a few positions. Setting --ratio1=0.99 will consider only these positions and greatly reduce the necessary amount of computation. This option refers to CRM models of size 1 (One binding site). (Note: This affects convergence time, and you can also set the number of EM iterations run during learning.) |
| -R, --ratio2 | Search ratio (|m|>1) | Same as --ratio1, but for CRM models with two or more binding sites. |
| -B, --binw | Distance histogram bin width | The distance distribution is a (smoothed) histogram over possible distances. It takes time to smooth, so for large sequences (kilobases) it is recommended that you "bin" together groups of this many consecutive base pairs. |
| -T, --tunerat | Tune set size | To avoid overfitting (or maybe you have too much data), you can hold aside this ratio of the training set for evaluation only. |
| --save | Save learned CRM to file | The file format for this is not meant to
be human readable, although it contains comments.
It is meant to be used in subsequent calls to the program with
the --load option
Note: the CRM file format for the --load and --save options
may change in future versions.
See also: the --load and --base options. |
| --load | Use a previously-learned CRM model | Instead of learning a model, read one from file and evaluate it Note: train/tune/test set divisions remain the same |
| --base | Supply a CRM submodel |
if the --base option is supplied with a filename,
the program will read the submodel and all
explored structures will contain this submodel
(i.e. all the binding sites of the submodel).
See also: The --badjust option. |
| -j, --badjust | Learn CRM submodel parameters |
If the program is given a CRM submodel to always use
(via the --base option), the parameters of this submodel
can be adjusted by the learning algorithm by setting this
boolean.
For instance, with [-j|--badjust] set, the program will consider this base submodel structure with the parameters as given, add a new binding site with randomized parameters, then learn all model parameters. Without this option set (default), the program will learn the parameters of any additional binding site(s), but not of the base submodel. See also: The --base option. |
The program writes both to standard error and standard output.
Written to standard error:
The following is example summary data written to standard error (--verbose=1):
[llama $] scrm2 positive.fa negative.fa -b fly.markov -N10 -F0 -T0.25 -I1 -Z4 -C2 -D2 -G1
Structured CRM 2.1
Inupt file(s): "positive.fa" "negative.fa"
Parameter settings: X="" b="fly.markov" c="" W="" V="" load="" save="" fileprec=10
f="" C=2 D=2 G=1 d=unset o=unset s=unset m=unset w=20 x=20 e=10
E=10 I=1 r=0.99 R=0.1 u=0.001 k=0.1 B=1 Z=4 N=10 F=0 T=0.25 S=-1 v=1
Seeding PRNG with 1147986514
Read order 5 Markov file "fly.markov". (0.023 seconds)
TRAINSET: 135 sequences (67+ 68- )
TUNESET: 45 sequences (23+ 22- )
TESTSET: 20 sequences (10+ 10- )
1 (TmhybCGGATATCCGbdnnh) F1 = 0.914398 > 0 (9.59 seconds)
2 (AwGCGCGGATATCCGndnnh | nnnCGGATATCCGndnnhnw) F1 = 0.966999 > 0.914398 (9.59 seconds)
3 (kymrATGGATATCCGndnnh) & (nnnnACTTnmGGGACTThnn) F1 = 0.9999 > 0.966999 (42.9 seconds)
4 (nnnnnCGGATATCCGndnnh) & (~wkrATsyGvTACTAGGvvGw) F1 = 0.956673 (50.3 seconds)
...
Each learned model is summarized (if --verbose=1) as:
The following is an example CRM model written to standard error:
Binding Site #1 (template 0.000998004)
Motif #1 (motif preference 1) Consensus GGkAbAGrCwswCGCknwyy MLE GGGATAGACTCTCGCGTATT
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A | 0.27 0.00 0.00 0.72 0.00 0.72 0.00 0.54 0.18 0.45 0.00 0.36 0.18 0.00 0.00 0.00 0.18 0.45 0.00 0.09
C | 0.09 0.00 0.00 0.09 0.36 0.00 0.27 0.00 0.72 0.09 0.45 0.09 0.72 0.00 0.90 0.09 0.18 0.18 0.36 0.45
G | 0.63 0.99 0.54 0.09 0.27 0.18 0.72 0.45 0.00 0.00 0.36 0.00 0.09 0.99 0.09 0.54 0.27 0.09 0.09 0.00
T | 0.00 0.00 0.45 0.09 0.36 0.09 0.00 0.00 0.09 0.45 0.18 0.54 0.00 0.00 0.00 0.36 0.36 0.27 0.54 0.45
Binding Site #2 (template 0.00751102)
Motif #1 (motif preference 0.5) Consensus ryTCmbCCdCTTCkwGGAdr MLE GTTCAGCCGCTTCGTGGATG
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A | 0.36 0.09 0.00 0.09 0.54 0.00 0.00 0.00 0.36 0.00 0.00 0.00 0.00 0.00 0.36 0.00 0.27 0.54 0.27 0.36
C | 0.00 0.36 0.27 0.63 0.27 0.36 0.90 0.90 0.00 0.99 0.18 0.00 0.72 0.18 0.00 0.00 0.00 0.18 0.00 0.00
G | 0.63 0.00 0.09 0.27 0.00 0.36 0.09 0.00 0.36 0.00 0.00 0.00 0.09 0.54 0.18 0.81 0.63 0.18 0.27 0.45
T | 0.00 0.54 0.63 0.00 0.18 0.27 0.00 0.09 0.27 0.00 0.81 0.99 0.18 0.27 0.45 0.18 0.09 0.09 0.45 0.18
Motif #2 (motif preference 0.5) Consensus TykTTGmTCArsmGCkwCrT MLE TCGTTGATCAGCAGCGACGT
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A | 0.18 0.18 0.09 0.18 0.27 0.00 0.45 0.00 0.27 0.72 0.27 0.09 0.45 0.00 0.00 0.00 0.54 0.18 0.36 0.18
C | 0.18 0.54 0.18 0.09 0.00 0.00 0.45 0.18 0.63 0.00 0.00 0.54 0.36 0.09 0.63 0.18 0.00 0.72 0.18 0.00
G | 0.09 0.00 0.45 0.00 0.00 0.99 0.00 0.18 0.09 0.00 0.54 0.36 0.18 0.90 0.27 0.45 0.00 0.00 0.45 0.00
T | 0.54 0.27 0.27 0.72 0.72 0.00 0.09 0.63 0.00 0.27 0.18 0.00 0.00 0.00 0.09 0.36 0.45 0.09 0.00 0.81
Negated Binding Site #1 (template 0.929835)
Motif #1 (motif preference 1) Consensus TTnnGGGACTThnnnnnnnn MLE TTACGGGACTTAGAACAACA
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
A | 0.00 0.00 0.30 0.26 0.02 0.00 0.02 0.98 0.00 0.01 0.00 0.35 0.28 0.30 0.29 0.23 0.33 0.30 0.19 0.31
C | 0.03 0.00 0.19 0.33 0.01 0.00 0.03 0.00 0.96 0.01 0.00 0.23 0.17 0.22 0.24 0.31 0.20 0.23 0.32 0.17
G | 0.00 0.00 0.25 0.19 0.95 0.98 0.93 0.01 0.00 0.00 0.00 0.17 0.31 0.19 0.20 0.21 0.20 0.16 0.16 0.21
T | 0.95 0.98 0.24 0.21 0.01 0.00 0.01 0.00 0.03 0.97 0.99 0.23 0.21 0.26 0.24 0.23 0.24 0.29 0.31 0.28
Binding Site #1 downstream of #2: 0.710477
Binding Site #1 downstream of #3: 0.500481
Binding Site #2 downstream of #3: 0.500681
Distance #1 <-> END as Distance[0..501) peak ~= 237, mid ~= 230
Distance #1 <-> #2 as Distance[0..501) peak ~= 136, mid ~= 173
Distance #1 <-> #3 as Distance[0..501) peak ~= 128, mid ~= 151
Distance #2 <-> END as Distance[0..501) peak ~= 394, mid ~= 308
Distance #2 <-> #3 as Distance[0..501) peak ~= 0, mid ~= 91
Distance #3 <-> END as Distance[0..501) peak ~= 0, mid ~= 100
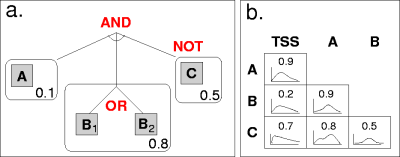
This has the same structure as shown in Figure 1.
Notes:
Standard output gets evaluation data, one record per sequence, one line per record with four fields (separated by white space):
Example output:
acCer1_sgdGene_YBR181C train 1 0.987643 2@172 1@201 acCer1_sgdGene_YBR188C train 1 0.98993 2@295 1@365 ... acCer1_sgdGene_YPR103W train 1 0.814915 2@250 1@315 acCer1_sgdGene_YJR072C train 0 2.76453e-05 2@3 1@76 acCer1_sgdGene_YGL213C train 0 0.000704786 2@65 1@298 acCer1_sgdGene_YOR190W train 0 0.0746866 2@12 1@93 ... acCer1_sgdGene_YGR057C train 0 0.00324076 2@133 1@201 acCer1_sgdGene_YBR085W tune 1 0.85638 2@201 1@426 acCer1_sgdGene_YBR191W tune 1 0.998627 2@141 1@193 ... acCer1_sgdGene_YPR132W tune 1 0.999275 2@82 1@115 acCer1_sgdGene_YGR250C tune 0 0.00647939 2@187 1@411 acCer1_sgdGene_YCR107W tune 0 0.00274947 2@27 1@272 ... acCer1_sgdGene_YMR016C tune 0 0.000158975 2@204 1@383 acCer1_sgdGene_YBL087C test 1 0.977379 2@148 1@427 acCer1_sgdGene_YDR471W test 1 0.923808 2@143 1@341 acCer1_sgdGene_YFL034W test 1 0.991551 2@191 1@304 acCer1_sgdGene_YGL030W test 1 0.997261 2@168 1@320 acCer1_sgdGene_YHR141C test 1 0.98651 2@133 1@474 acCer1_sgdGene_YJL190C test 1 0.927052 2@225 1@254 acCer1_sgdGene_YLR048W test 1 0.995488 2@70 1@144 acCer1_sgdGene_YLR448W test 1 0.99195 2@61 1@246 acCer1_sgdGene_YNL302C test 1 0.999094 2@108 1@177 acCer1_sgdGene_YOR095C test 1 0.000222165 2@106 1@209 acCer1_sgdGene_YPR102C test 1 0.953526 2@21 1@49 acCer1_sgdGene_YGL066W test 0 0.00928651 2@139 1@182 acCer1_sgdGene_YGR287C test 0 4.81675e-05 2@9 1@32 acCer1_sgdGene_YDR071C test 0 0.647564 2@113 1@423 acCer1_sgdGene_YBR141C test 0 0.00608682 2@270 1@372 acCer1_sgdGene_YER069W test 0 0.049907 2@283 1@487 acCer1_sgdGene_YMR144W test 0 0.699687 2@206 1@322 acCer1_sgdGene_YOR162C test 0 0.40865 2@21 1@47 acCer1_sgdGene_YJL140W test 0 0.00721103 2@12 1@38 acCer1_sgdGene_YIL115C test 0 0.0228935 2@275 1@365 acCer1_sgdGene_YIL067C test 0 0.014081 2@100 1@220
An example CRM model structure is shown in Figure 1. On the left (a), we see an example model structure: A conjuction of binding sites, each a disjunction of motifs. Binding sites also have a strand preference (a single number representing the probability that binding occurs on the template strand). Binding sites may be negated.
In this particular case, there are three binding sites. The first has a single motif ("A"), the second has two motifs (either "B1" or "B2" will satisfy this binding site), and the third has a single motif ("C"), but is negated. This means that a positive seqeunce must contain the first two binding sites, but not the third. (A negative sequence would contain all three, or fail to contain one of the first two.)
On the right in Figure 1 (b), we see pairwise preferences: For each pair of binding sites,
Basic algorithm:
untilstopping criteria: Consider a model structure Learn parameters for said structure Evaluate modelreturnbest model
And slightly more detailed algorithm:
Q ← { }; (Empty queue)
for each candidate motif, c:
Create a single-motif model m with c;
Learn parameters of m;
Q ← Q ∪ m
for init iterations: (Some user-defined number)
Create a random single-motif model, m;
Learn parameters of m;
Q ← Q ∪ m
until stopping criteria: (e.g. A user-defined maximum number of models considered)
m ← best model from Q;
m' ← m ∪ new random single-motif binding site;
Learn parameters of m';
Q ← Q ∪ m'
m' ← m ∪ with new random motif adding to last binding site;
Learn parameters of m';
Q ← Q ∪ m'
m' ← m ∪ new random single-motif negated binding site;
Learn parameters of m';
Q ← Q ∪ m'
return best model considered.
Notes:
The file metric.cpp has a function, double metric(const
vector<pair<probability, probability> >&) which is given
a set of (class, prediction) pairs, and returns a "score" (typically between 0
and 1, higher is better). "class" refers to the true class of the example (1.0
is positive, 0.0 is negative, but these can be "soft"--between 0 and 1).
"prediction" refers to the prediction made by the learning algorithm (which
will be "soft"--the probability of an example being generated by a positive
path through the corresponding HMM). (Note that probability is a
type, defined in probabilty.h.)
You may create any metric you like, or call one of the existing ones, such
as metric_cmargin (classification margin), metric_Fx
(F1), or metric_acc (plain old accuracy).
Note that you should also update the function (also in
metric.cpp), std::string metric(), which returns the
"name" of the metric (which will be printed to standard error during the
learning process).
The file, custom.cpp is designed to make it easy to customize the learning task by explicity constraining (or otherwise altering) the structure and/or parameters of CRM models, or by constraining other probabilities, like the probability distribution over possible orders-of-binding-sites.
These are the "custom" functions:
void constrain_preconditions(CRM &crm, vector<Example*> &training_data):
This is called before the first iteration of EM-based parameter learning algorithm (see our paper, Noto & Craven, ECCB 2006 and Krogh et al., ICPR 1994). You can put any code here to constrain or otherwise alter a CRM model.
void constrain_per_iteration(CRM &crm, vector<Example*> &training_data):
This is called after each E-M iteration.
void constrain_finalize(CRM &crm, vector<Example*> &training_data):
This is called after all E-M iterations.
void constrain_order(list<pair<vector<uint>, probability> > &order, const CRM&):
This is called whenever the CRM learner needs to know the probability of a given ordering among binding sites. It's based on normalizing the product of all pairwise orderings, but you can change the answer before it is given to the learning algorithm.
Typical use would be to force certain binding sites to be adjacent by zeroing-out inconsistent orderings, then renormalizing.
The three versions of constrain_..., might all do the same thing, of course.
Examples of use might be: