Let A and B be finite, disjoint point sets in n-dimensional Euclidean space, represented by the m x n and k x n matrices A and B, respectively. The MSM-T algorithm generates a decision tree representing the planes needed to separate the sets A and B . Each non-leaf node in the tree is plane that further separates A and B . Each leaf node contains points of either A or B exclusively (or to a prescribed tolerance). For a detailed description of the MSM-T algorithm, see:
The MATLAB representation of the matrices A and B (from now on denoted by A and B), must be placed in the MATLAB environment. This can be done either by actually entering them by hand, or by placing them in an M-file and loading the M-file into the MATLAB environment.
The decision tree is technically represented as a matrix in the MATLAB environment. This matrix representation of the decision tree must be generated. To generate this matrix, call (in the MATLAB environment):
T = msmt_tree(A,B,max_depth,tolerance,certainty_factor,min_points)
In the above expression the various symbols are defined as follows:
See msmt_tree.m file.
The decision tree generated by the call above can be displayed graphically by calling the following routine (within the MATLAB environment):
disp_tree(T,A,B)
where:
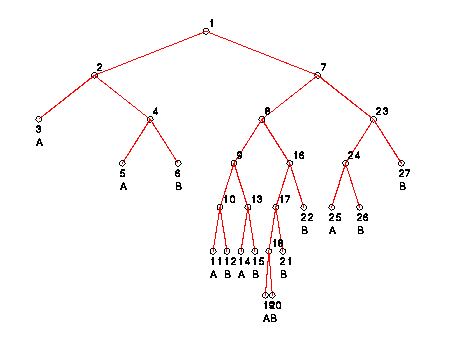
The following is an example of the graphical representation of the decision tree using Wisconsin Breast Cancer data.

Each node in the tree is numbered. In the MATLAB environment, the following information is provided:
See disp_tree.m file.
Pruning removes potentially unnecessary subtrees from the decision tree. This MATLAB implementation allows for pruning using 2 different algorithms: (1) Error-based pruning from C4.5: Programs for Machine Learning, and (2) Minimum misclassified points algorithm.
To prune the given decision tree using the error-based pruning algorithm (outlined in C4.5: Programs for Machine Learning), call (in the MATLAB environment):
T = prune_tree_C45(T,A,B,certainty_factor)
where:
The decision tree may also be pruned by this algorithm when the tree is generated by giving a value for certainty_factor in the call:
T = msmt_tree(A,B,max_depth,tolerance, certainty_factor, min_points)
For a detailed description of the pruning algorithm, see
See prune_tree_C45.m file.
The minimum misclassified points algorithm works as follows. An integer number of allowable misclassified points is given. If a plane is generated that splits a node and has less than this number of allowable misclassified points, this decision node is made into a leaf node. If the plane generated splits more than this allowable number of misclassified points, this decision node remains. This pruning algorithm can be called (in the MATLAB environment) by:
T = prune_tree_points(T,A,B,min_points)
where:
The decision tree may be pruned using this algorithm when it is generated by giving a value for min_points in the call:
T = msmt_tree(A,B,max_depth,tolerance, certainty_factor, min_points)
See prune_tree_points.m file.
The performance of the MSM-T algorithm on a given data set may be tested by cross-validation. The cross-validation procedure works as follows. The sets A and B are equally divided into a given number of groups (num_groups); for each group, a decision tree is constructed using (num_groups - 1) groups. The tree is then tested using the group set aside. The algorithm returns percent (percentage of correctly classified points by the MSM-T algorithm), confusion_matrix (see cross_val.m file), ave_planes (average number of planes needed in the separation). The cross-validation procedure can be initiated by making the following call (in the MATLAB environment):
[percent,confusion_matrix,ave_planes] = cross_val(A,B,num_groups,max_depth,tolerance,certainty_factor,min_points)
where:
See cross_val.m file.
A decision tree may be written to any specified file using the following call (in the MATLAB environment):
msmt_write_file(T,'filename')
where:
Once a tree has been written, it can be retrieved and put back in the MATLAB environment with the following call (in the MATLAB environment):
T = msmt_read_file('filename')
where:
See msmt_write_file.m and msmt_read_file.m files.