Comparison: Adjacency list vs adjacency matrix
To compare the two ways of representing edges, we will consider both the
amount of space used, and the time required for some standard operations.
Regardless of which way edges are represented, O(N) space will be needed
to store information about the nodes (the space for the node objects
themselves, plus the array or linked list of pointers to the nodes).
In addition,
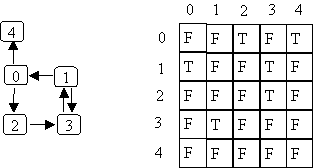
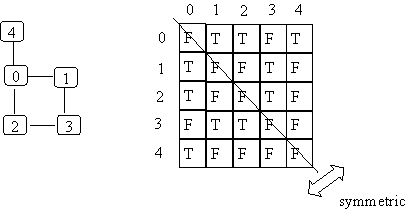
an adjacency matrix takes O(N2) space for a graph with N nodes,
regardless of how many edges are in the graph.
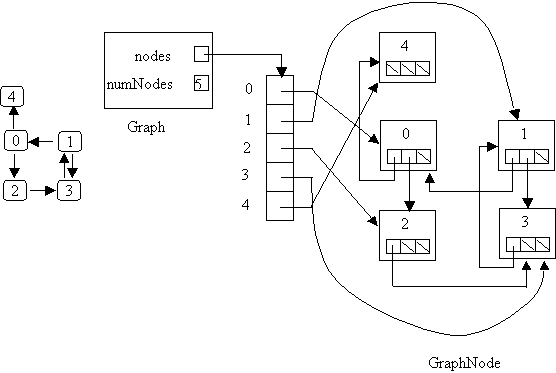
Assuming that adjacency lists are implemented using Sequences, the space
used to store information about edges
is proportional to N + E (where E is the number of edges).
The N comes from the fact that every node has a Sequence (so some space
is taken up even if the node has no successors);
the E comes from the fact that the space required for a Sequence of
k items is O(k).
If the graph is sparse (there are not many edges), then adjacency lists
will probably be more space efficient than adjacency matrices;
if the graph is dense (the number of edges is O(N2)), then
the adjacency matrix will probably be more space efficient.
The following table provides information about time requirements for
some simple graph operations.
N is the number of nodes in the graph.
You should think about each operation and be sure that you understand
why its time requirements are as specified in the table.