Heap Sort

Contents

• Heap Review
• Heap Sort
• Heap Complexity

Heap Review

Remember that a heap is a way to implement a priority queue.

The property of a priority queue is:

• when you get an item it is the one with the highest priority

Heaps have same complexity as a balanced search tree but:

• they can easily be kept in an array
• they are much simpler than a balanced search tree
• they are cheaper to run in practice

A heap is a binary tree that has special structure compared to a general binary tree:

1. The root is greater than any value in a subtree

• this means the highest priority is at the root
• this is less information than a BST and this is why it can be easier and faster

• the height is always log(n) so all operations are O(log(n))

Heap Sort

If you have values in a heap and remove them one at a time they come out in (reverse) sorted order. Since a heap has worst case complexity of O(log(n)) it can get O(nlog(n)) to remove n value that are sorted.

There are a few areas that we want to make this work well:

• how do we form the heap efficiently?
• how can we use the input array to avoid extra memory usage?
• how do we get the result in the normal sorted order?

If we achieve it all then we have a worst case O(nlog(n)) sort that does not use extra memory. This is the best theoretically for a comparison sort.

The steps of the heap sort algorithm are:

1. Use data to form a heap
2. remove highest priority item from heap (largest)
3. reform heap with remaining data

You repeat steps 2 & 3 until you finish all the data.

You could do step 1 by inserting the items one at a time into the heap:

• This would be O(nlog(n)). Turns out we can do in O(n). This does not change the overall complexity but is more efficient.
• You would have to modify the normal heap implementation to avoid needing a second array.

Instead we will enter all values and make it into a heap in one pass.

As with other heap operations, we first make it a complete binary tree and then fix up so the ordering is correct. We have already seen that there is a relationship between a complete binary tree and an array.

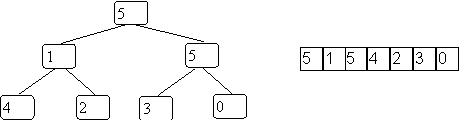
Our standard sorting example becomes:

Now we need to get the ordering correct.

It will work by letting the smaller values percolate down the tree.

To make into a heap you use an algorithm that fixes the lower part of the tree and works it way toward the root:

• Go from lowest right parent (non-leaf) and proceed to left. When finish one level go to next starting again from right.

• at each node, percolate down the item to its proper place in this part of the subtree, e.g., subheap.

Here is how the example goes:

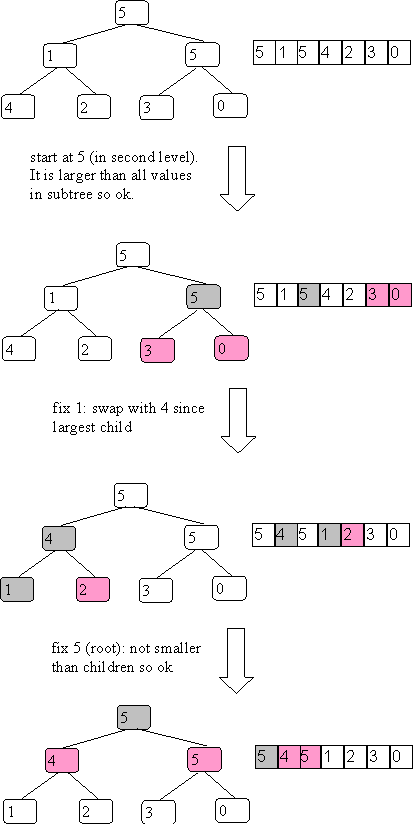
This example has very few swaps. In some cases you have to percolate a value down by swapping it with several children.

The Weiss book has the details to show that this is worst case O(n) complexity. It isn't O(nlog(n)) because each step is log(subtree height currently considering) and most of the nodes root subtrees with a small height. For example, about half the nodes have no children (are leaves).

Now that we have a heap, we just remove the items one after another.

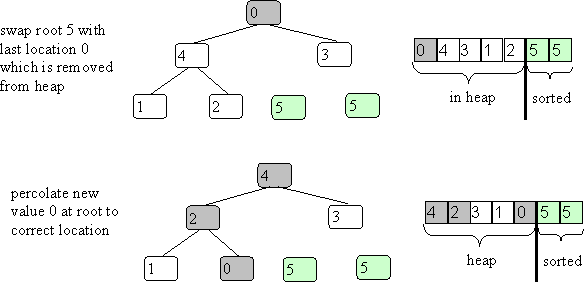
The only new twist here is to keep the removed item in the space of the original array. To do this you swap the largest item (at root) with the last item (lower right in heap). In our example this gives:

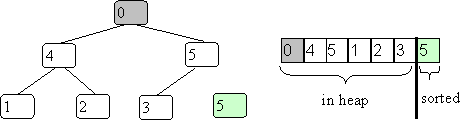
The last value of 5 is no longer in the heap.

Now let the new value at the root percolate down to where it belongs.

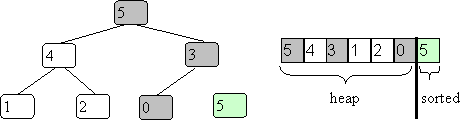
Now repeat with the new root value (just chance it is 5 again):

And keep continuing:

Heap Complexity

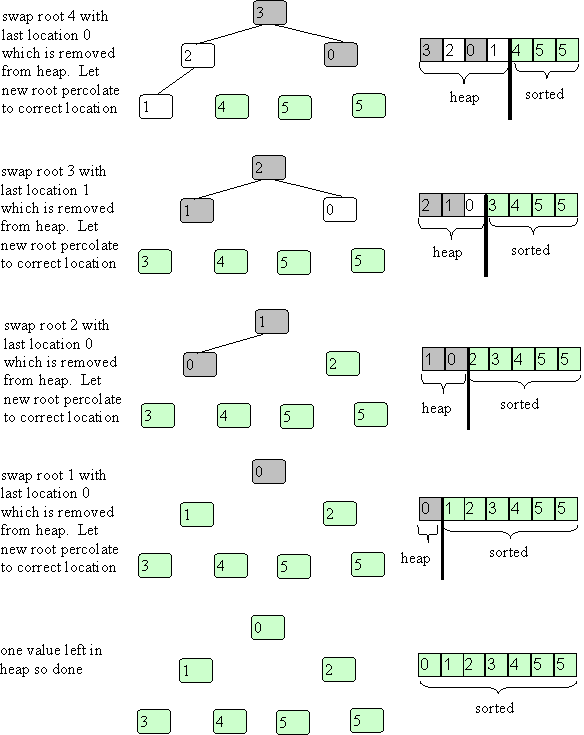
The part just shown very similar to removal from a heap which is O(log(n)). You do it n-1 times so it is O(nlog(n)). The last steps are cheaper but for the reverse reason from the building of the heap, most are log(n) so it is O(nlog(n)) overall for this part. The build part was O(n) so it does not dominate. For the whole heap sort you get O(nlog(n)).

There is no extra memory except a few for local temporaries.

Thus, we have finally achieved a comparison sort that uses no extra memory and is O(nlog(n)) in the worst case.

In many cases people still use quick sort because it uses no extra memory and is usually O(nlog(n)). Quick sort runs faster than heap sort in practice. The worst case of O(n²) is not seen in practice.