
The previous set of notes discussed how to implement the ListADT interface using an array to store the items in the list. Here we discuss how to implement the ListADT interface using a linked list to store the items. However, before talking about linked lists, we will review the difference between primitive and non-primitive types in Java.
Java has two "categories" of types:
When you declare a variable with a primitive type, you get enough space to hold a value of that type. Here's some code involving a primitive type, and the corresponding conceptual picture:

When you declare a variable with a reference type, you get space for a reference (or pointer) to that type, not for the type itself. You must use "new" to get space for the type itself. This is illustrated below.

Remember that class objects are also reference types. For example, if you declare a variable of type List, you only get space for a pointer to a list; no actual list exists until you use "new". This is illustrated below, assuming the array implementation of lists, and assuming that the List constructor initializes the items array to be of size 3. Note that because it is an array of Objects, each array element is (automatically) initialized to null (shown using a diagonal line in the picture).

An important consequence of the fact that non-primitive types are really pointers is that assigning from one variable to another can cause aliasing (two different names refer to the same object). For example:

Note that in this example, the assignment to B[1] changed not only that value, but also the value in A[1] (because A and B were pointing to the same array)! However, an assignment to B itself (not to an element of the array pointed to by B) has no effect on A:

A similar situation arises when a non-primitive value is passed as an argument to a method. For example, consider the following 4 statements, and the definition of method changeArray:
1. int[] A = new int[3];
2. A[1] = 6;
3. changeArray(A);
4. System.out.print(A[1]);
5. public static void changeArray(int[] X) {
6. X[1] = 10;
7. X = new int[2];
8. }
The picture below illustrates what happens when this code executes.

Note that the method call causes A and X to be aliases (they both point to the same array). Therefore, the assignment X[1] = 10 changes both X[1] and A[1]. However, the assignment X = new int[2] only changes X, not A, so when the call to changeArray finishes, the value of A[1] is still 10, not 0.
TEST YOURSELF #1
For each line of the code shown below, draw the corresponding conceptual picture.
int [] X = new int[2]; X[0] = 1; int Y = new int[3]; Y[0] = 2; Y = X; Y[0] = 3;

Note that a linked list consists of one or more nodes. Each node contains some data (in this example, item 1, item 2, etc,) and a pointer. For each node other than the last one, the pointer points to the next node in the list. For the last node, the pointer is null (indicated in the example using a diagonal line). To implement linked lists in Java, we will define a Listnode class, to be used to represent the individual nodes of the list.
public class Listnode {
//*** fields ***
private Object data;
private Listnode next;
//*** methods ***
// 2 constructors
public Listnode(Object d) {
this(d, null);
}
public Listnode(Object d, Listnode n) {
data = d;
next = n;
}
// access to fields
public Object getData() {
return data;
}
public Listnode getNext() {
return next;
}
// modify fields
public void setData(Object ob) {
data = ob;
}
public void setNext(Listnode n) {
next = n;
}
}
To understand this better, consider writing code to create a linked list with two nodes, containing "ant" and "bat", respectively, pointed to by a variable named L. First we need to declare variable L; here's the declaration together with a picture showing what we have so far:

To make L point to the first node of the list, we need to use new to allocate space for that node. We want its data field to contain "ant" and (for now) we don't care about its next field, so we'll use the 1-argument Listnode constructor (which sets the next field to null):

To add the second node to the end of the list we need to create the new node (with "bat" in its data field and null in its next field), and we need to set the next field of the first node to point to the new one:

TEST YOURSELF #2
Assume that the list shown above (with nodes "ant" and "bat") has been created.
Question 1.
Write code to change the contents of the second node's data field from
"bat" to "cat".
Question 2.
Write code to insert a new node with "rat" in its data field
between the two existing nodes.

And here's the code:
Note that it is vital to first copy the value of n's
next field
into tmp's next field (step 2(a)) before setting
n's next field to point to the new node (step 2(b)).
If we set n's next field first, we would lose our
only pointer to the rest of the list after node n!
Also note that, in order to follow the steps shown in the picture
above, we needed to use variable tmp to create the new node
(in the picture, step 1 shows the new node just "floating" there, but
that isn't possible -- we need to have some variable point to it so
that we can set its next field, and so that we can set
n's next field to point to it).
However, we could in fact accomplish steps 1 and 2 with a single
statement that creates the new node, fills in its data and
next fields, and sets n's next field
to point to the new node!
Here is that amazing statement:
Draw pictures like the ones given above, to illustrate what happens
when node n is the last node in the list.
Does the statement
Now consider the worst-case running time for this add operation.
Whether we use the single statement or the list of three statements,
we are really doing the same thing:
Listnode tmp = new Listnode(newdat); // Step 1
tmp.setNext( n.getNext() ); // Step 2(a)
n.setNext( tmp ); // Step 2(b)
n.setNext( new Listnode(newdat, n.getNext()) ); // steps 1, 2(a), and 2(b)
n.setNext( new Listnode(newdat, n.getNext()) );
still work correctly?
We will assume that storage allocation via new takes constant time.
Setting the values of the three fields also takes constant time,
so the whole operation is a constant-time (O(1)) operation.
In particular, the time required to add a new node immediately after
a given node is independent of
the number of nodes already in the list.
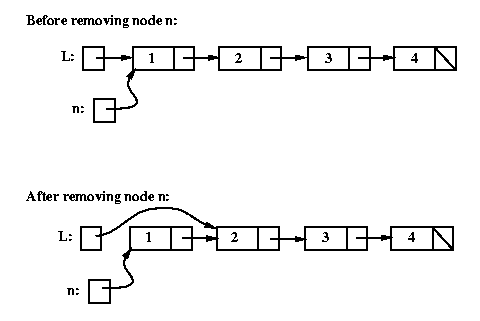
Removing a node
To remove a given node n from a linked list, we need to
change the next field of the node that comes immediately
before n in the list to point to whatever n's
next field was pointing to.
Here's the conceptual picture:

Note that the fact that n's next field is still pointing to a node in the list doesn't matter -- n has been removed from the list, because it cannot be reached from L. It should be clear that in order to implement the remove operation, we first need to have a pointer to the node before node n (because that node's next field has to be changed). The only way to get to that node is to start at the beginning of the list. We want to keep moving along the list as long as the current node's next field is not pointing to node n. Here's the appropriate code:
Listnode tmp = L; while (tmp.getNext() != n) tmp = tmp.getNext(); // find the node before n
Note that this kind of code (moving along a list until some condition holds) is very common. For example, similar code would be used to implement a lookup operation on a linked list (an operation that determines whether there is a node in the list that contains a given piece of data).
Note also that there is one case when the code given above will not work. When n is the very first node in the list, the picture is like this:

In this case, the test (tmp.getNext() != n) will always be false, and eventually we will "fall off the end" of the list (i.e., tmp will become null, and we will get a runtime error when we try to dereference a null pointer). We will take care of that case in a minute; first, assuming that n is not the first node in the list, here's the code that removes n from the list:
Listnode tmp = L; while (tmp.getNext() != n) tmp = tmp.getNext(); // find the node before n tmp.setNext( n.getNext() ); // remove n from the linked list
How can we test whether n is the first node in the list, and what should we do in that case? If n is the first node, then L will be pointing to it, so we can test whether L == n. The following before and after pictures illustrate removing node n when it is the first node in the list:
Here's the complete code for removing node n from a linked list,
including the special case when n is the first node in the list:
What is the worst-case running time for this remove operation?
If node n is the first node in the list, then we simply
change one field (L's next field).
However, in the general case, we must traverse the list to find the
node before n, and in the worst case (when n is the
last node in the list), this requires time proportional to
the number of nodes in the list.
Once the node before n is found, the remove operation involves
just one assignment (to the next field of that node), which
takes constant time.
So the worst-case time running time for this operation on a list with N
nodes is O(N).
Note that
if your linked lists do include a header node, there is no need for the
special case code given above for the remove operation;
node n can never be the first node in the list, so there
is no need to check for that case.
Similarly, having a header node can simplify the code that adds a node
before a given node n.
Note that if you do decide to use a header node, you must remember
to initialize an empty list to contain one (dummy) node, you must
remember not to include the header node in the count of "real" nodes in the
list (e.g., if you implement a size operation), and you must
remember to ignore the header node in operations like contains.
Look back at the definition of
the ArrayList class in
the second set of notes and think about which fields and/or methods
need to be changed before reading any further.
Clearly, the type of the items field needs to change, since the
items will no longer be stored in an array;
instead, the items will be stored in a linked list.
Since having a header node simplifies the add and remove
operations, we will assume that the linked list has a header node,
Here's new declaration for the items field:
Given this declaration for the items field,
let's think again about the three List methods
that were discussed assuming the array implementation:
The disadvantage of this approach is that it requires O(N) time to add a
node to the end of a list with N items.
An alternative is to add a lastNode field (often called a
tail pointer) to the LinkedList class,
and to implement the methods that modify the linked list so that
lastNode always points to the last node in the linked list
(which will be the header node if the list is empty).
There is more opportunity for error (since several methods will need to
ensure that the lastNode field is kept up to date), but the
use of the lastNode field will mean that the worst-case running time
for this version of add is always O(1), and that will be
important for applications that frequently add to the end of a list
(which is often a common operation).
Here's a picture of the "ant, bat, cat" list, when
the implementation includes a lastNode pointer:
TEST YOURSELF #4
if (L == n) {
// special case: n is the first node in the list
L = n.getNext();
} else {
// general case: find the node before n, then "unlink" n
Listnode tmp = L;
while (tmp.getNext() != n) tmp = tmp.getNext();
tmp.setNext( n.getNext() );
}
Using a header node
There is an alternative to writing special-case code to handle removing
the first node in a list.
That alternative is to use a header node: a dummy node at the
front of the list that is there only to reduce the need for special-case
code in the linked-list operations.
For example, the picture below shows how the list "ant", "bat", "cat", would
be represented using a linked list without and with a header node:

The LinkedList Class
Now let's consider how to implement our ListADT interface using linked list instead of arrays;
i.e., how to implement a scaled-down LinkedList class.
Remember, we only want to change the implementation (the "internal"
part of the List abstract data type), not the interface (the
"external" part of the abstract data type).
That means that the signatures of the public methods for the LinkedList
class will be the same as the ones for the ArrayList class
and the descriptions of what those methods do will also be the same.
The only thing that will change is how the list is represented,
and how the methods are implemented.
private Listnode items; // pointer to the header node of the list of items
add (to end of list)
Recall that the first version of method add adds a given value
to the end of the list.
We have already discussed how to add a new node to a linked list following
a given node.
The only question is how best to handle adding a new node at the end
of the list.
A straightforward approach would be to traverse the list, looking for
the last node (i.e., use a variable tmp as was done above
in the code that looked for the node before node n).
Once the last node is found, the new node can be inserted immediately after it.

Write the "add at the end" method (assuming that the LinkedList class includes both a header node and a lastNode field).
TEST YOURSELF #5
Write the "add at a given position" method (assuming that the LinkedList class includes both a header node and a lastNode field).
TEST YOURSELF #6
Write the constructor.
In terms of ease of implementation, straightforward implementations of both the array and linked-list versions seem reasonably easy. However, the methods for the linked-list version seem to require more special cases.
TEST YOURSELF #7
Assume that lists are implemented using linked lists. How much time is required (using Big-O notation) to remove the first item from a list? to remove the last item from a list? How do these times compare to the times required for the same operations when the list is implemented using an array?
Another way to fix the problem is to use a doubly linked list. Here's the conceptual picture:

Each node in a doubly linked list contains three fields: the data, and two pointers. One pointer points to the previous node in the list, and the other pointer points to the next node in the list. The previous pointer of the first node, and the next pointer of the last node are both null. Here's the Java class definition for a doubly linked list node:
public class DblListnode {
//*** fields ***
private DblListnode prev;
private Object data;
private DblListnode next;
//*** methods ***
// 3 constructors
public DblListnode() {
this(null, null, null);
}
public DblListnode(Object d) {
this(null, d, null);
}
public DblListnode(DblListnode p, Object d, DblListnode n) {
prev = p;
data = d;
next = n;
}
// access to fields
public Object getData() {
return data;
}
public DblListnode getNext() {
return next;
}
public DblListnode getPrev() {
return prev;
}
// modify fields
public void setData(Object ob) {
data = ob;
}
public void setNext(DblListnode n) {
next = n;
}
public void setPrev(DblListnode p) {
prev = p;
}
}
To remove a given node n from a doubly linked list, we need to change the prev field of the node to its right, and we need to change the next field of the node to its left, as illustrated below.

Here's the code for removing node n:
// Step 1: change the prev field of the node after n DblListnode tmp = n.getNext(); tmp.setPrev( n.getPrev() ); // Step 2: change the next field of the node before n tmp = n.getPrev(); tmp.setNext( n.getNext() );Unfortunately, this code doesn't work (causes an attempt to dereference a null pointer) if n is either the first or the last node in the list. We can add code to test for these special cases, or we can use a circular, doubly linked list, as discussed below.

The class definitions are the same as for the non-circular versions. The difference is that, instead of being null, the next field of the last node points to the first node, and (for doubly linked circular lists) the prev field of the first node points to the last node.
The code given above for removing node n from a doubly linked list will work correctly except when node n is the first node in the list. In that case, the variable L that points to the first node in the list needs to be updated, so special-case code will always be needed unless the list includes a header node.
Another issue that you must address if you use a circular linked list is that if you're not careful, you may end up going round and round in circles! For example, what happens if you try to search for a particular value val using code like this:
Listnode tmp = L; while (tmp != null && !tmp.getData().equals(val)) tmp = tmp.getNext();and the value is not in the list? You will have an infinite loop!
Write the correct code to search for value val in a circular linked list pointed to by L. (Assume that the list contains no null data values.)
The major advantage of doubly linked lists is that they make some operations (like the removal of a given node, or a right-to-left traversal of the list) more efficient.
The major advantage of circular lists (over non-circular lists) is that they eliminate some special-case code for some operations. Also, some applications lead naturally to circular list representations. For example, a computer network might best be modeled using a circular list.