RED-BLACK TREES

A Red black tree is a type of tree data structure. It is basically a Binary Search tree that has both red and black colored nodes that follow a certain set of properties. Below is an image that shows how a Red-black tree looks like:

To better understand the existence of such a tree, let us dive into the properties of a red-black tree.

Properties of a Red-black tree:

1. It follows all properties of a Binary Search tree.
2. Every node is either red-colored or black-colored
3. The root node is always a black node.
4. A red node cannot have a red child.
5. Every possible path from the root node to any leaf node in the tree consists of the same number of black nodes.

This is an example of a valid RBT (short for red-black tree):

Red-black tree operations:

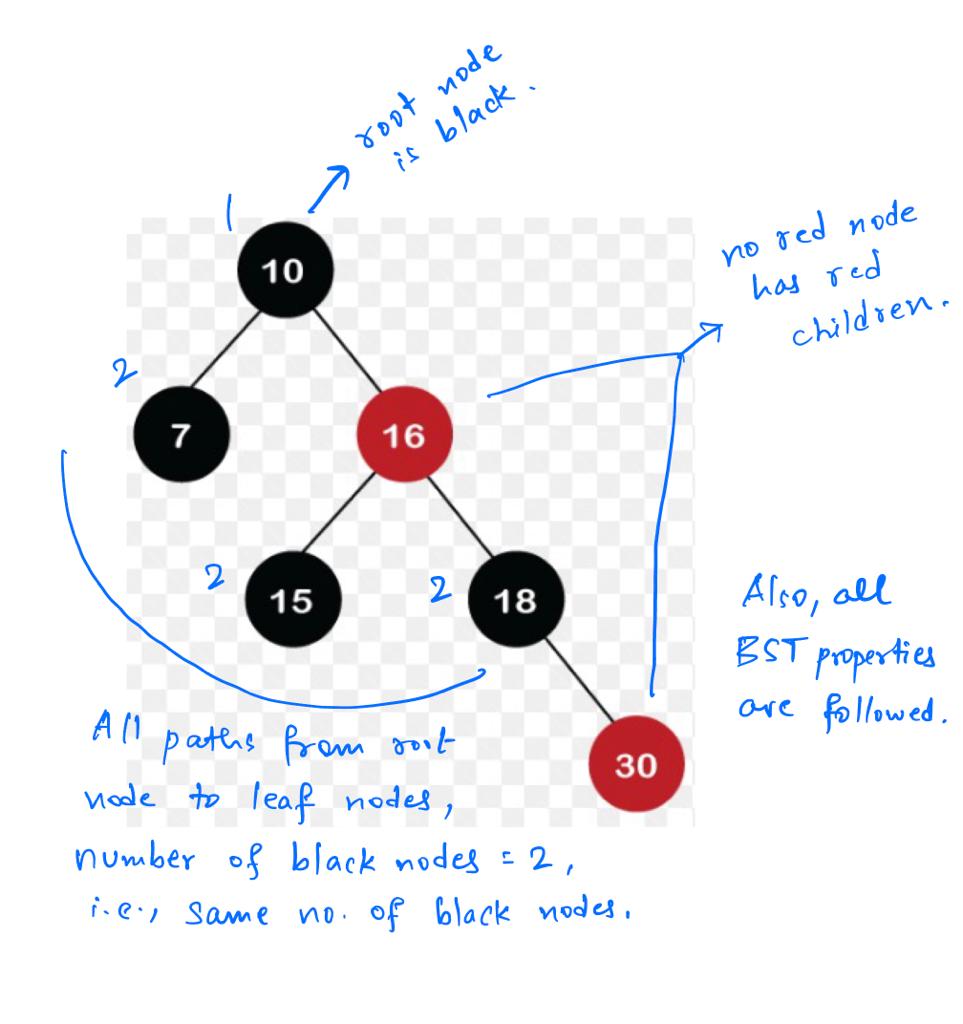
You can perform three simple operations on a red-black tree:

• Insertion of a red or black node.
• Searching for a red or black node.
• Deleting a red or black node.

In all of these operations, the insert and delete operations modify the tree, which may cause changes in the properties of the red-black tree too. Thus, we should also take care of fixing the tree and restoring all its properties so that it remains as a red-black tree. For that, there is a fix algorithm in place that traverses through the entire modified tree and changes position and color of the nodes so that it follows the properties of a red-black tree as indicated in the previous section above.

Worst-case Complexities:

• Insert: O(log(N))
• Search: O(log(N))
• Delete: O(log(N))

where N is the number of nodes in the red-black tree.