Red-Black Trees

A red-black trees is a self-balancing binary search tree in which every node is colored with either red or black. The tree adjusts itself automatically after each insertion or deletion operation by coloring each node in the tree either red or black.

Properties of Red-Black Trees

• Each node is either red or black.
• The root is always black.
• Red nodes can not have red children.
• Every path from root to a null child has the same number of black nodes.
• Null children are black.

How to insert into a Red-Black Tree:

1. Insert new key using BST insertion algorithm
2. Color new node red
3. Check red black tree properties and restore if necessary

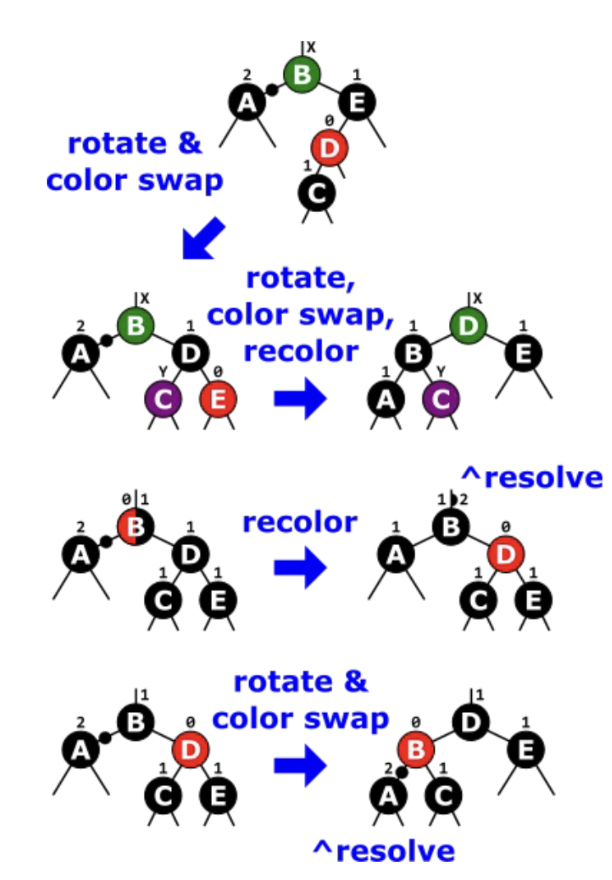
Tips for repairing an insertion

• Root is red: switch to black.
• Red node with red child, and aunt is black (or null): rotate and color swap.
• Red node with red child, and aunt is red: recolor

How to delete from a Red-Black Tree:

1. Delete key using BST deletion algorithm
2. Check red black tree properties and restore if necessary

Tips for repairing a deletion

• Deleted node is black and replacement is red: turn replacement black.
• If not, some rotation and color swaps need to be performed.

Learn More