


Next: Experimental Results
Up: Level Set Method for
Previous: Theory
This section will give an algorithmic summary of the level set method for shape modeling.
- Calculate the image gradient at each point in the image.
- Initialize
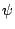 . This is done by first making
. This is done by first making 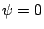 at the points specified by the user in the
initial boundary. The value of
at the points specified by the user in the
initial boundary. The value of 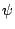 at all the other points is
at all the other points is
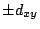 , where
, where 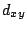 is the distance of point
is the distance of point
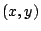 from the closest point on the level set
from the closest point on the level set 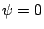 . The value is positive or negative depending on whether
the point is outside or inside the boundary.
. The value is positive or negative depending on whether
the point is outside or inside the boundary.
- Calculate the velocity at the points on the level set
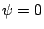 using the equations given in the previous
section. The velocity of other points is equal to the velocity of the closest point on the level set
using the equations given in the previous
section. The velocity of other points is equal to the velocity of the closest point on the level set 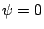 .
This step is knows as extending the velocity. This is done because, the curvature term is defined only on the front,
so it does not make sense to calculate velocities at every point but it should only be calculated at the front.
.
This step is knows as extending the velocity. This is done because, the curvature term is defined only on the front,
so it does not make sense to calculate velocities at every point but it should only be calculated at the front.
- Use the velocities to update the function
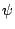 using equation 4.
using equation 4.
- Repeat steps 2 through 4 till the solution converges or for a fixed (large) number of iterations.
- The function
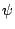 is reinitialized every fixed number of iterations to the signed distance function.
is reinitialized every fixed number of iterations to the signed distance function.



Next: Experimental Results
Up: Level Set Method for
Previous: Theory
Saurabh Goyal
2003-12-16