An Introduction to B-Trees

What are B-Trees?

Search Trees that have a degree ≥2 (maximum # of children)
Access and insertion similar to BSTs
Obey BST order property

Different B-Trees can have different degrees:

• Degree m is the maximum number of children beneath any node.
  -> Efficient access for a chunk of data

• The maximum number of values in any node is m-1
• Internal nodes (non-root and non-leaf) must have atleast m/2 children
• Internal nodes with k children, have k-1 values

What are 2-3-4 Trees?

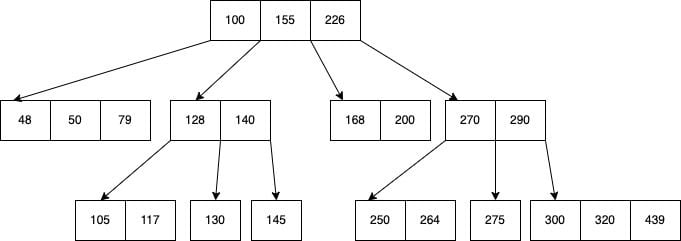
B-Trees with a degree of 4
2-3-4 denotes the number of children a node can have

2-3-4 Tree Insertion Algorithm

Important: we only add values to the bottom of the tree i.e. only in leaf nodes.

1. If there is space in the node, add it.
2. If there is no space in the node, split the leaf node and push the middle value to the parent node.

Premptive Split

On the way down to the leaf node that you are inserting a value into, split any node that you step through which is full.
This helps ensure that there is always space in the parent of any potentially split child node to hold one more value.

The parent node can never be full:

• While inserting a new node, in the way, preemptively split a node that is full
• Makes sure that we are never inserting into a node that has a full parent
• Internal nodes with k children, have k-1 values

You may find more information here.