Google Foobar

Exploring my journey through Google’s Foobar coding challenge

It seems like unlike everyone else on the internet, I didn’t know what Google Foobar is. I just found myself working on a project at 2am, looking something up, when my browser split in half, asking me if I was “up for a challenge”. After a little googling, I realized this was some sort of coding challenge by Google with something about saving bunnies. Interesting enough for me to click “I want to play” before turning in for the night.

I woke up the next morning to find myself greeted by a Unix-like shell with some standard Unix commands. The challenge itself was broken up into levels, with 1 challenge in levels 1 and 5, 2 challenges in levels 2 and 4, and 3 challenges in level 3 (as I later found out), which are below in chronological order. Intrigued, I requested the first challenge and got to work.

The cake is not a lie!

The first problem was fairly simple, asking us to split a circular string into the maximum number of equal parts such that there is no leftover in the string. The circular string part doesn’t actually matter at all; abcabc (abc|abc, thus 2), rotated to cabcab, can still be divided cab|cab (still 2). As with most string problems, the solution ended up being a double pointer. The forward pointer moves forward at every time step, whereas the back pointer only moves forward when its character is the same as the forward pointer’s character, ensuring \(\Theta(n)\). This works because the back pointer only moves forward when it is checking if there is a loop and the front pointer defines the front of the loop when the back pointer is not moving.

def solution(s):
    if len(s) < 1: return 0
    if len(s) == 1: return 1

    p1 = 0
    p2 = 1
    orig = 1

    while p2 < len(s):
        while s[p1] != s[p2]:
            p2 += 1
            if p2 >= len(s):
                return 1

        if len(s)%p2 == 0:
            orig = p2
            while p2 < len(s) and s[p1] == s[p2]:
                p1 += 1
                p2 += 1
            if p2 >= len(s):
                return int(len(s)/orig)

        p1 = 0
        p2 += 1

    return 1

As a side note, I omit code comments, original problem statements, and the story for brevity. I will attach a repo that contains the original code, the problem statements, and the story at the bottom of this post if you wish to refer to the original.

Bunny Prisoner Locating

The start of level 2, still fairly simple. We are asked to devise a solution where given coordinates \((x,y)\), we return a cell number, where cells are filled in a triangular fashion (for example, the first 10 cells)

7
4 8
2 5 9
1 3 6 10

There is a clear pattern here. From the first cell, we can obtain any cell, given \(x=1\), by \(1+ y *(y-1) / 2\). Similarly, we can obtain any horizontal cell, given \(y=1\), using \(x * (x+1)/2\). Combining these two equations, with an adjustment factor to account for not basing off of cell \(1\) every time, we may obtain the solution.

def num(x,y):
    return str(((y*y+2*y*x-3*y+x*x-x)/2)+1)

This question came down to some basic pattern recognition and knowledge of how to add series of numbers; there is no knowledge of algorithms needed. At this point, I was really starting to question whether it was even worth the little break time I was allotting to it.

Gearing Up for Destruction

We are given positions of pegs on a number line. We must then put gears on every single one of these pegs such that the last gear moves twice as fast (is half the size of) the first gear. We return the size of the first gear as a fraction that fulfills these requirements, if possible.

I usually find it helpful to draw a basic diagram in these cases. As a side note, sketches in this post were taken directly from my notes so please excuse any lack of cleanliness in the sketches.

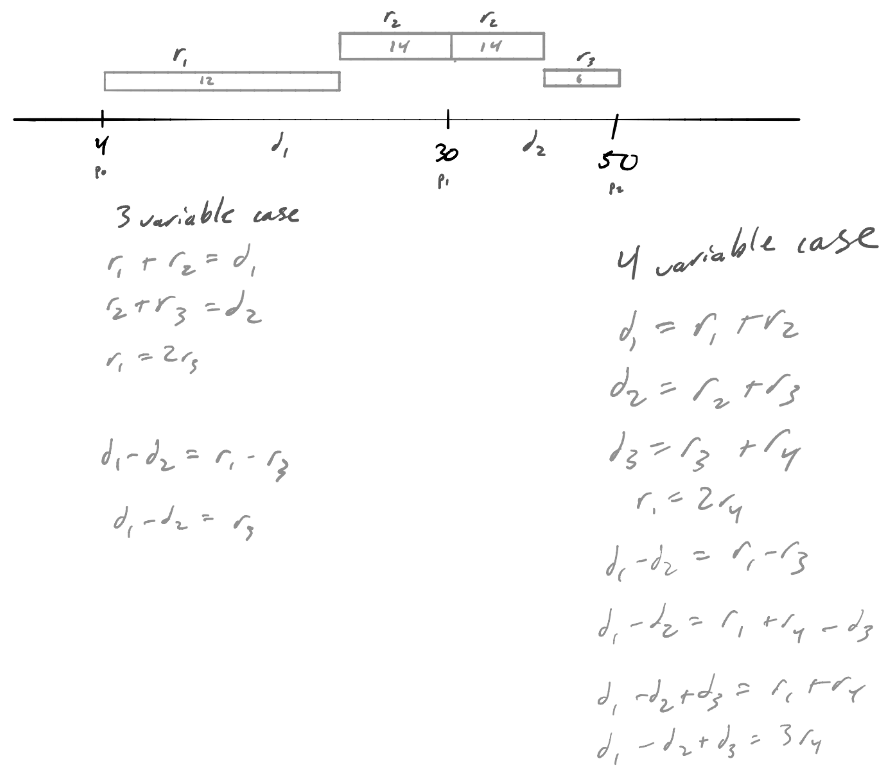
Thus, with some simple math, we can see that we can obtain \(r_1\) directly from the distance between the pegs, calculated by \(d_1 - d_2 + d_3 - d_4 + ... + s * d_n\) where \(s=-1 + n\ (\mathrm{mod}\ 2)\), contingent on some trivial error checking. To round it off, I wanted to use the peg positions (\(p_0, p_1, ..., p_n\)) rather than the distances between the pegs. The math for that is slightly messier (longer), so I omit that; feel free to take a stab at it yourself.

def solution(pegs):
    prop_sol = 2*(sum(pegs[1::2]) - sum(pegs[::2])) + pegs[0]

    if len(pegs) % 2 == 0:
        prop_sol = 2* (prop_sol - pegs[-1])
        if prop_sol/3 < 1:
            return [-1,-1]
        if prop_sol % 3 == 0:
            ret_val = [prop_sol/3,1]
        else:
            ret_val = [prop_sol,3]
    else:
        prop_sol = 2* (prop_sol + pegs[-1])
        if prop_sol < 1:
            return [-1,-1]
        else:
            ret_val = [prop_sol, 1]
    last_gear = ret_val[0]/ret_val[1]
    for i in range(len(pegs)-1):
        last_gear = pegs[i+1]-pegs[i] - last_gear
        if last_gear < 1:
            return [-1,-1]
    return ret_val

Not terribly difficult as a whole, although it was much easier once sketched out. Mainly just going through the math. At the start, I was concerned about displaying the value as a fraction - it makes the problem more annoying - but it turned out not to matter when using the peg positions (\(p_i\)) rather than the distance values (\(d_i\)). On to level 3!

Fuel Injection Perfection

This is the first problem that really gave me trouble, albeit because I requested the problem and was unable to even look at it until quite a bit later, when I had almost run out of time (at which point the shell had some technical issues that I’ll detail later).

The problem gives us an input number and asks us to determine the fastest way of reducing said number to \(1\), using only 3 operations: \(+1\), \(-1\) and \(\div 2\) (although this can only be used when the number is even). I imagine this problem as a Collatz conjecture-esque tree, where we want to get onto the main branch of \(2^n\) as fast as possible (or secondarily to any even number). Looking at it from a binary perspective, it makes sense that if the last 2 digits are \(01\), we would subtract instead of add (we get 2 division operations instead of 1), and if the last 2 bits are \(11\), we would add (we, again, get more division operations). There is an edge case where if \(n=3\), we subtract instead of add.

def solution(n):
    n = int(n)
    i = 0
    while n > 1:
        if (n&1) == 0:
            n >>= 1
        elif (n&3) == 1 or n == 3:
            n -= 1
        else:
            n += 1
        i += 1
    return i

I had actually done this in Java originally (mainly to just have a go with Java), but foobar seemed to be having some problem parsing Java. I couldn’t get it to work and I was almost out of time, so I ended up scrapping the Java program and rewriting it in Python. I decided to just stick with Python here on out, as foobar seemed to like Python much better.

Find the Access Codes

This one is fairly trivial to solve. We have to find the number of lucky triples \((x,y,z)\) in a list of numbers such that \(y\ (\mathrm{mod}\ x) = 0\), \(z\ (\mathrm{mod}\ y) = 0\), and \(x_i < y_i < z_i\) where \(x_i\) is the index of \(x\).

This is a fairly textbook dynamic programming problem, where we would calculate the “lucky doubles” and then calculate the lucky triples off of those.

def solution(l):
    trips = 0
    doubs = [0]*len(l)

    for i in range(1, len(l)):
        for j in range(i):
            if l[i] % l[j] == 0:
                doubs[i] += 1
                trips += doubs[j]
    return trips

This solution does multicount sets if there is a repeated number. For example, [1,1,2,4] will double count the lucky triple of [1,2,4] as there are 2 1 values. I tried a solution where the lucky triples are not multicounted, but it failed a test. Given this, I would venture to guess that the above is the answer Google wanted, although being forced to remove the multicount would have been much more interesting; it would force people to think through the edge cases and [1,2,4] is the same no matter what index the one is pulled from (it doesn’t even make sense when given the story).

Doomsday Fuel

This problem is finally a step, albeit a small one, up from the other problems. We are given a matrix of values where each row is a state and each value in that row corresponds with the probability of going to that state (\(a_{ij}\) is the probability of going from state \(i\) to state \(j\)). We return the probability of each final state, all over a common denominator.

 [[0,1,0,0,0,1],  # s0
  [4,0,0,3,2,0],  # s1
  [0,0,0,0,0,0],  # s2
  [0,0,0,0,0,0],  # s3
  [0,0,0,0,0,0],  # s4
  [0,0,0,0,0,0]]  # s5

s0, the initial state, goes to s1 and s5 with equal probability
s1 can become s0, s3, or s4, but with different probabilities
s2 is terminal, and unreachable (never observed in practice)
s3 is terminal
s4 is terminal
s5 is terminal

If we trace the probabilities of landing in each state, we get s2: 0; s3: 3/14; s4: 1/7; s5: 9/14
Converting to common denominator and displaying in the form
[s2.numerator, s3.numerator, s4.numerator, s5.numerator, denominator], we get
[0, 3, 2, 9, 14]

This requires some linear algebra, but we can implement a modification of an Absorbing Markov Chain solution.

We first standardize the weights as percentages and then model the matrix as below.

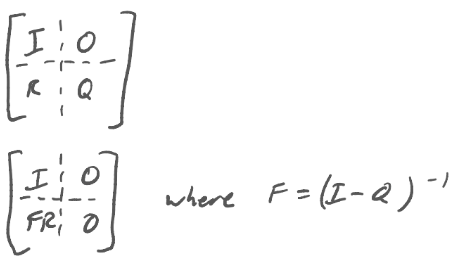
The FR submatrix gives us the probability of reaching each state from every other state. Thus, we really only need the s0 row matrix transformation. My code calculates the full FR submatrix for modularity, although it can easily be optimized to only calculate the s0 row matrix.

from fractions import Fraction
import numpy as np

def solution(m):
    if len(m) < 2:
        return [1,1]
    r_subm, q_subm = split_martix(m)
    f_subm = calc_f(q_subm)
    fr_subm = np.dot(f_subm, r_subm)
    return dec_to_frac_with_lcm(fr_subm[0])

def split_martix(m):
    absorbing = set()
    for row_i in range(len(m)):
        if sum(m[row_i]) == 0:
            absorbing.add(row_i)
    r_subm = []
    q_subm = []
    for row_i in range(len(m)):
        if row_i not in absorbing:
            row_total = float(sum(m[row_i]))
            r_temp = []
            q_temp = []
            for col_i in range(len(m[row_i])):
                if col_i in absorbing:
                    r_temp.append(m[row_i][col_i]/row_total)
                else:
                    q_temp.append(m[row_i][col_i]/row_total)
            r_subm.append(r_temp)
            q_subm.append(q_temp)
    return r_subm, q_subm

def calc_f(q_subm):
    return np.linalg.inv(np.subtract(np.identity(len(q_subm)), q_subm))

def dec_to_frac_with_lcm(l):
    ret_arr = []
    denoms = []
    for num in l:
        frac = Fraction(num).limit_denominator()
        ret_arr.append(frac.numerator)
        denoms.append(frac.denominator)
    lcd = 1
    for denom in denoms:
        lcd = lcm(lcd,denom)
    for num_i in range(len(ret_arr)):
        ret_arr[num_i] *= int(lcd/denoms[num_i])
    ret_arr.append(lcd)
    return ret_arr

And with that, we’re finished with Level 3. At this point, a dialogue appears to send your information to a Google recruiter. If we assume the problems people talk online about equally sample the problems people do, it seems like most people drop off here. We, though, forge on to level 4!

Distract the Guards

So remember how I said Doomsday Fuel was finally a small step up? This is a MASSIVE step up. Foobar goes 0 to 60 really quickly. The challenges from here on are really quite interesting.

In this problem, we have a bunch of guards that gamble bananas on thumb wrestling. We know that they always bet the number of bananas the guard with fewer bananas has and that the guard with more bananas always gets overconfident and always loses. We want to ensure that they never have the same number of bananas, as they would then stop playing and go back to guarding bunnies (we’re breaking bunnies out of jail at this point in the story). We are given a list of the number of bananas each guard has and we want to return the number of guards that cannot be placed into infinite loops.

The naïve solution, while simple, is terribly inefficient; we can do better. We break this problem into 2 subproblems - whether 2 guards will loop or not and how to match guards such that we have the least guards not in a loop.

Working out the math, we find that guards loop when the sum of the reduced pair of numbers is not a power of 2. I omit the proof as it is rather long, but I encourage you to work through a few different examples and convince yourself of this. Thus, we run through all possibilities to get a matrix of guards that will loop with each other.

We can then convert this matrix to a graph. Finding out which guards to match now becomes a maximum matching problem. While I implemented a relatively naïve approach to maximum matching, we can implement much better solutions. The Blossom algorithm is the most common algorithm for maximum matching, as it supports weights, and runs in \(O(V^2 E)\). We, however, do not have weights on our graph, so we may use something like Micali-Vazirani (1980), which runs in \(O(V^{0.5} E)\) and doesn’t allow weights, or Gabow-Tarjan (1990), which is also \(O(V^{0.5} E)\) but only allows integer weights. All of the above, however, are rather long and foobar has a max limit on the amount of code one can input.

def solution(l):
    g = generate_graph(l)
    matches = reduce(g)
    return len(l) - matches

def loop(x,y):
    base = int((x+y)/gcd(x,y))
    return bool(base & (base - 1))

def gcd(a,b):
    while b:
        a, b = b, a % b
    return a

def generate_graph(l):
    G = {i: [] for i in range(len(l))}
    for i in range(len(l)):
        for j in range(i, len(l)):
            if i != j and loop(l[i], l[j]):
                G[i].append(j)
                G[j].append(i)
    return G

def reduce(g):
    matched = 0
    checks = len(g[max(g, key=lambda key: len(g[key]))])
    while len(g) > 1 and checks >= 1:
        init_mw_node = min(g, key=lambda key: len(g[key]))
        if (len(g[init_mw_node])) < 1 :
            del g[init_mw_node]
        else:
            temp_sec_min = [len(g[g[init_mw_node][0]])+1,1]
            for node_i in g[init_mw_node]:
                if len(g[node_i]) < temp_sec_min[0]:
                    temp_sec_min = [len(g[node_i]), node_i]
                for check_i in range(len(g[node_i])):
                    if g[node_i][check_i] == init_mw_node:
                        del g[node_i][check_i]
                        break
            for node_i in g[temp_sec_min[1]]:
                for check_i in range(len(g[node_i])):
                    if g[node_i][check_i] == temp_sec_min[1]:
                        del g[node_i][check_i]
                        break
            del g[init_mw_node]
            del g[temp_sec_min[1]]
            matched += 2
        if len(g) > 1:
            checks = len(g[max(g, key=lambda key: len(g[key]))])
    return matched

While the problem sounds easy at first read, this problem was the first where I felt really excited about completing it. I ended up actually reading through Micali-Vazirani (1980) and thought about implementing it before realizing that foobar probably did not need that level of optimization.

Bringing a Gun to a Guard Fight

I really want to know who’s designed this problem. I have so many questions about why and how this person came up with this problem. It has to be the type of problem that somebody gives you once and you become determined to pass it on so someone else can live through the same experience.

The problem puts you and a guard into a room with mirrors on all 4 walls. You can then shoot a laser gun that goes some maximum distance and your objective is to find the different number of ways you can hit the guard.

While one might jump to the naïve solution of checking every angle from which you can fire, this would not work as there are an infinite number of angles you can fire and you might step over some solution. Thus, the solution of this problem comes with the key intuition that reflecting the laser is the same as reflecting the room and letting the laser travel in a straight line.

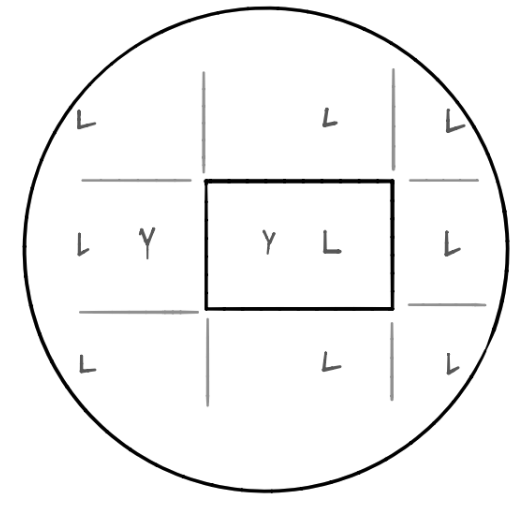
Thus, if we reflect the room such that we generate all possible guard positions (\(L\)) within the radius of the shot, it becomes a simple matter of counting the number of guards we can shoot. There is one complication, that we cannot shoot one person through another person. In the sketch above, both guard positions (\(L\)) in the middle row at both the left and right side as thus unreachable; to hit the left guard position you would shoot through yourself (\(Y\)) and to hit the right guard position you would shoot through the guard in the original room. To solve this, we simply count the number of unique angles we can shoot the guard at.

from math import ceil, sqrt, atan2

def solution(dimensions, your_position, guard_position, distance):
    locations = reflection_map(dimensions, your_position, guard_position, distance)
    angles = set()
    shoot_count = 0
    for point in locations:
        if dist(point, your_position) <= distance:
            angle = atan2(point[1]-your_position[1], point[0]-your_position[0])
            if angle not in angles:
                angles.add(angle)
                if point[2] == 1:
                    shoot_count += 1
        else:
            break
    return shoot_count

def reflection_map(dimensions, your_position, guard_position, distance):
    locations = []
    x_repls = int(ceil((your_position[0]+distance)/float(dimensions[0])))
    y_repls = int(ceil((your_position[1]+distance)/float(dimensions[1])))
    for i in range(x_repls):
        x_add = your_position[0] if i%2==0 else dimensions[0]-your_position[0]
        xg_add = guard_position[0] if i%2==0 else dimensions[0]-guard_position[0]
        for j in range(y_repls):
            y_add = your_position[1] if j%2==0 else dimensions[1]-your_position[1]
            yg_add = guard_position[1] if j%2==0 else dimensions[1]-guard_position[1]
            fq_point = [(dimensions[0]*i) + x_add, (dimensions[1]*j) + y_add, 0]
            fqg_point = [(dimensions[0]*i) + xg_add, (dimensions[1]*j) + yg_add, 1]
            locations.extend((fq_point, fqg_point,
                [-1*fq_point[0],fq_point[1],fq_point[2]],
                [-1*fqg_point[0],fqg_point[1],fqg_point[2]],
                [fq_point[0],-1*fq_point[1],fq_point[2]],
                [fqg_point[0],-1*fqg_point[1],fqg_point[2]],
                [-1*fq_point[0],-1*fq_point[1],fq_point[2]],
                [-1*fqg_point[0],-1*fqg_point[1],fqg_point[2]]))
    del locations[0]
    locations.sort(key=lambda x: dist(x,your_position))
    return locations

def dist(l1, l2):
    return sqrt(float((l1[0]-l2[0]))**2 + (l1[1]-l2[1])**2)

This problem ended up having a few annoying edge cases I don’t detail here, but they’re probably visible if you trace the code (or go to the repo linked at the bottom and read the code comments). Anyways, onto level 5, the final level.

Expanding Nebula

Oh boy was this a ride. This problem was the cherry on top for this entire challenge. It was the first one I really had to close my computer and mull over how to do this efficiently.

This is a cellular automata problem where we are given an \(m \times n\) binary matrix and are tasked with finding out the number of previous states (1 time step prior) that could result in the input matrix. To understand how \(a_{ij}\) evolves at every time step, we look at \(a_{ij}\), \(a_{i+1, j}\), \(a_{i, j+1}\), and \(a_{i+1, j+1}\). If the sum of these entries is exactly \(1\), \(a_{ij}\) becomes \(1\) in the next time step. In all other cases, \(a_{ij}\) becomes \(0\) in the next time step. Because we cannot calculate the next time step for any \(a_{mj}\) or \(a_{in}\), we drop the bottom and right row and column respectively in each time step.

I went about solving it by first brute force generating all the preimages for each column. Each \(m \times 1\) column matrix has preimages of form \((m+1) \times 2\). We may then represent each \((m+1) \times 2\) preimage as an ordered pair of integers, where each entry in the column is a bit and the whole becomes a binary representation of an integer. Thus, we have integer ordered pair preimages for each column.

We can then pairwise check whether each ordered pair preimage is able to match up with the next column’s ordered pair preimages by checking if the preimages share the appropriate integer (ordered pairs \((a,b)\) and \((c,d)\) can only combine into an ordered triple \((a,b,d)\) if \(b=c\)). We can then employ dynamic programming to further optimize our program by ensuring that we are not checking every single possible route, but are relying on previous calculations to count the number of paths.

def solution(g):
    transposed = tuple(zip(*g))
    preimgs = precol(transposed[0])
    precount = dict()
    for pair in preimgs:
        precount[pair[0]] = 1
    for col in transposed:
        preimgs = precol(col)
        count = dict()
        for pair in preimgs:
            if pair[0] not in precount: precount[pair[0]] = 0
            if pair[1] not in count: count[pair[1]] = 0
            count[pair[1]] += precount[pair[0]]
        precount = count
    return sum(precount.values())


def precol(col):
    possib = ((0, 0), (0, 1), (1, 0), (1, 1))
    curr = devol[col[0]]
    for i in range(1, len(col)):
        new = []
        for tes in curr:
            for comb in possib:
                if evol[(tes[i], comb)] == col[i]:
                    new.append(tes+(comb,))
        curr = tuple(new)
    bin_ret = [tuple(zip(*i)) for i in curr]
    return [tuple([bitlist(nu) for nu in possibl]) for possibl in bin_ret]

def bitlist(bitsl):
    out = 0
    for bit in bitsl:
        out = (out << 1) | bit
    return out

evol = {((0, 0), (0, 0)): 0, ((0, 0), (0, 1)): 1, ((0, 0), (1, 0)): 1,
        ((0, 0), (1, 1)): 0, ((0, 1), (0, 0)): 1, ((0, 1), (0, 1)): 0,
        ((0, 1), (1, 0)): 0, ((0, 1), (1, 1)): 0, ((1, 0), (0, 0)): 1,
        ((1, 0), (0, 1)): 0, ((1, 0), (1, 0)): 0, ((1, 0), (1, 1)): 0,
        ((1, 1), (0, 0)): 0, ((1, 1), (0, 1)): 0, ((1, 1), (1, 0)): 0,
        ((1, 1), (1, 1)): 0}
devol = {0: (((0, 0), (0, 0)), ((0, 0), (1, 1)), ((0, 1), (0, 1)),
             ((0, 1), (1, 0)), ((0, 1), (1, 1)), ((1, 0), (0, 1)),
             ((1, 0), (1, 0)), ((1, 0), (1, 1)), ((1, 1), (0, 0)),
             ((1, 1), (0, 1)), ((1, 1), (1, 0)), ((1, 1), (1, 1))),
         1: (((1, 0), (0, 0)), ((0, 1), (0, 0)), ((0, 0), (1, 0)),
             ((0, 0), (0, 1)))}

The hardest part of this problem was just figuring out how to get under the time limit. That being said, this is by no means the cleanest way to do it, nor I suspect the most efficient way to do it. I suspect the main optimization would come from generating each individual column preimage. I did not optimize this as foobar caps the column height (\(m\)) at 10, making it bounded \(NP\). We could apply a similar dynamic programming technique to generating column preimages, although I’m not altogether convinced that this is the best way to do it. If you do manage to come up with a better way to do this, please do drop me a message.

Conclusion

Wow. We’re done. I almost can’t believe it. This took me ages to finish as I was just working on it during my free time and breaks during the day.

As a final challenge, foobar gives a little ciphertext at the end. It’s not an official challenge by foobar in the manner that the others are, but an easter egg mini challenge at the end. The ciphertext is just XORed with my username and then encoded with base64. Doing the same in reverse gives us

{'success' : 'great', 'colleague' : 'esteemed', 'efforts' : 'incredible', 'achievement' : 'unlocked', 'rabbits' : 'safe', 'foo' : 'win!'}

In any case, I hope I didn’t condense the problems too much and that they’re still understandable. Given the length of the post, all the examples and story that foobar gives seemed unnecessary. My code was definitely messier than usual, but I started this mainly as algorithm practice and wrote this up because of the last couple levels. The first 2 levels of problems were quite simple, but I could definitely see people using them as a live algorithm test for interviews to see how one thinks. Level 3 wasn’t terribly difficult either, although I don’t think the last level 3 problem would be a good live interview question. I am, however, surprised that they would use the first 3 levels as an asynchronous algorithm recruiting tool, as it seems fairly trivial given the large amount of time allotted per question. Levels 4 and 5 actually got interesting, where I had to make sure I’m checking my edge cases and working through the problem fully. I almost wish that they had less challenges (9 got a little much), but made them all level 4/5 difficult. I would say this was a fun but trivial experience, but the back half was not at all trivial. Seriously, when actually doing this, it felt like going from Mario 1-1 to Dark Souls in one level.

That being said, the challenge was definitely cool start to finish — from the browser opening up and taking me to a Unix shell in browser that gave me challenges to the ending problems, and the story throughout it. It was like a clearweb, sanitized Cicada 3301.

On a closing note, my full code, if you decide to go read it after this already incredibly long post, contains some details I skimmed over in the explanations; I tried to capture as much of what foobar gave as possible in the repo, so feel free to peruse it if curious about the intricacies of foobar.