Projects in preparation

This page includes certain highlights of ongoing projects. As these materials have not yet been published, please refer to this page should you need to use or duplicate any of the materials contained here.

Multigrid solvers for elasticity

A soft deformable dragon figurine, using co-rotated linear elasticity. The embedding lattice (right) contains 402K cells.

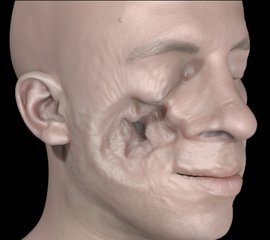
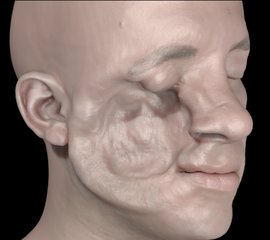
An object (not pictured) impacts a deformable face model at very high velocity. Flesh volume embedded in a lattice with 915K cells.

Hybrid hand simulation

A hybrid of cloth simulation, volumetric simulation of nonlinear flesh, soft constraints and contact/collision handling is used to animate a detailed hand model able to develop sharp features while respecting volume preservation.

A Second Order Virtual Node Method for Poisson Interface Problems on Irregular Domains

Abstract: We present a second order accurate, geometrically flexible and easy to implement method for solving the variable coefficient Poisson equation with interfacial discontinuities on an irregular domain. We discretize the equations using an embedded approach on a uniform Cartesian grid employing virtual nodes at interfaces and boundaries. A variational method is used to define numerical stencils near these special virtual nodes and a Lagrange multiplier approach is used to enforce jump conditions and Dirichlet boundary conditions. Our combination of these two aspects yields a symmetric positive definite discretization. In the general case, we obtain the standard 5-point stencil away from the interface. For the specific case of interface problems with continuous coefficients, we present a discontinuity removal technique that admits use of the standard 5-point finite difference stencil everywhere in the domain. Numerical experiments indicate second order accuracy in L-infinity.

Simulating crack propagation with XFEM and a hybrid mesh

Abstract: We present a method for simulating quasistatic crack propagation in 2-D which combines the extended finite element method (XFEM) with a general algorithm for cutting triangulated domains, and introduce a simple yet general and flexible quadrature rule based on the same geometric algorithm. The combination of these methods gives several advantages. First, the cutting algorithm provides a flexible and systematic way of determining material connectivity, which is required by the XFEM enrichment functions. Also, our integration scheme is straightfoward to implement and accurate, without requiring a triangulation that incorporates the new crack edges or the addition of new degrees of freedom to the system.