Longitudinal brain connectivity analysis via coupled harmonic bases
Abstract. There is a great deal of interest in using large scale
brain imaging studies to understand how brain connectivity
evolves over time for an individual and how it varies over
different levels/quantiles of cognitive function. To do so,
one typically performs so-called tractography procedures
on diffusion MR brain images and derives measures of brain
connectivity expressed as graphs. The nodes correspond to
distinct brain regions and the edges encode the strength of
the connection. The scientific interest is in characterizing
the evolution of these graphs over time or from healthy individuals
to diseased. We pose this important question in
terms of the Laplacian of the connectivity graphs derived
from various longitudinal or disease time points - quantifying
its progression is then expressed in terms of coupling
the harmonic bases of a full set of Laplacians. We derive
a coupled system of generalized eigenvalue problems (and
corresponding numerical optimization schemes) whose solution
helps characterize the full life cycle of brain connectivity
evolution in a given dataset. Finally, we show a set
of results on a diffusion MR imaging dataset of middle aged
people at risk for Alzheimer's disease (AD), who are cognitively
healthy. In such asymptomatic adults, we find that
a framework for characterizing brain connectivity evolution
provides the ability to predict cognitive scores for individual
subjects, and for estimating the progression of participant's
brain connectivity into the future.
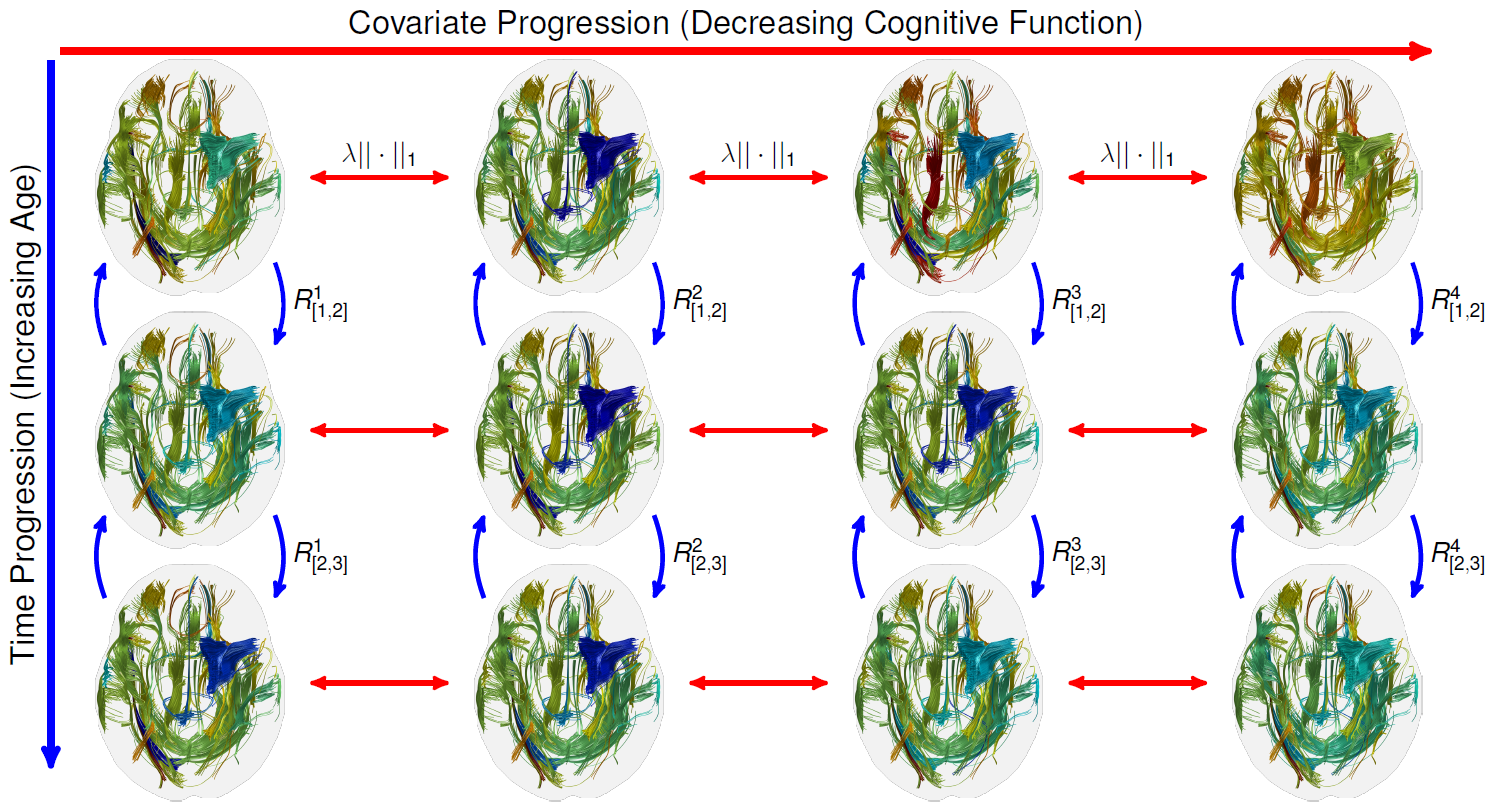 Figure: The evolution of top 50 most changing fiber tracts of the real data derived from the coupled harmonic bases. The tract colors represent their strong (blue) and
weak (red) connectivity strengths. Cross-sectional coupling (red arrows) via l-norm in each row. Longitudinal coupling (blue arrows) via rotation constraints in each column.
Figure: The evolution of top 50 most changing fiber tracts of the real data derived from the coupled harmonic bases. The tract colors represent their strong (blue) and
weak (red) connectivity strengths. Cross-sectional coupling (red arrows) via l-norm in each row. Longitudinal coupling (blue arrows) via rotation constraints in each column.
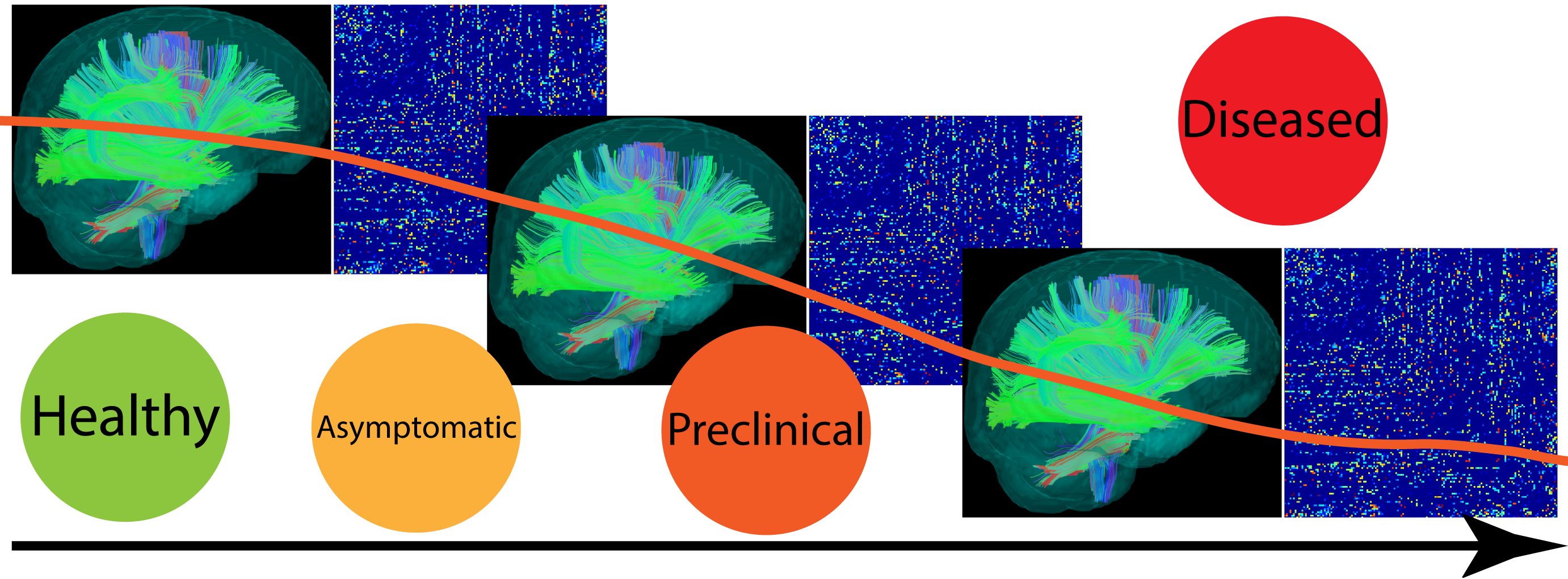 Figure: Brain connectivity evolves as the cognitive stage changes from healthy to diseased.
Figure: Brain connectivity evolves as the cognitive stage changes from healthy to diseased.
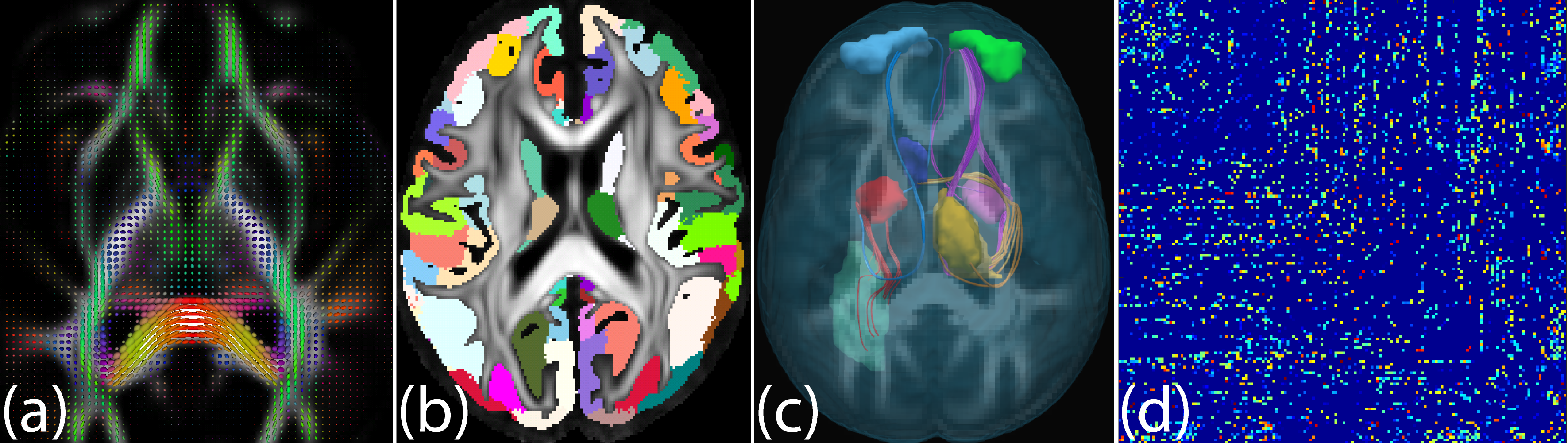 Figure: From brain image to adjacency matrix: (a) Diffusion tensor ellipsoids from dMRI. (b)
Gray matter regions as meaningful graph nodes. (c) Fiber tracts (axonal pathways between
brain regions) estimated via tractography as graph edges between gray matter nodes. (d)
Symmetric adjacency matrix representation of the graph.
References:
[1] Seong Jae Hwang, Nagesh Adluru, Maxwell D. Collins, Sathya N. Ravi, Barbara B. Bendlin, Sterling C. Johnson, Vikas Singh,
"Coupled Harmonic Bases for Longitudinal Characterization of Brain Networks",
Computer Vision and Pattern Recognition (CVPR), 2016.
[pdf]
[supplementary]
[poster]
[code will be available here]
[MATLAB toolbox for high quality fiber tract 3D visualization]
Acknowledgment:
SJH was supported by a University of Wisconsin CIBM fellowship (5T15LM007359-14). We acknowledge
support from NIH R01 AG040396 (VS), NIH R01 AG027161 (SCJ), NIH R01 AG37639 (BBB), NSF CCF
1320755 (VS), NSF CAREER award 1252725 (VS), UW ADRC AG033514, UW ICTR 1UL1RR025011,
Waisman Core grant P30 HD003352-45 and UW CPCP AI117924.
Figure: From brain image to adjacency matrix: (a) Diffusion tensor ellipsoids from dMRI. (b)
Gray matter regions as meaningful graph nodes. (c) Fiber tracts (axonal pathways between
brain regions) estimated via tractography as graph edges between gray matter nodes. (d)
Symmetric adjacency matrix representation of the graph.
References:
[1] Seong Jae Hwang, Nagesh Adluru, Maxwell D. Collins, Sathya N. Ravi, Barbara B. Bendlin, Sterling C. Johnson, Vikas Singh,
"Coupled Harmonic Bases for Longitudinal Characterization of Brain Networks",
Computer Vision and Pattern Recognition (CVPR), 2016.
[pdf]
[supplementary]
[poster]
[code will be available here]
[MATLAB toolbox for high quality fiber tract 3D visualization]
Acknowledgment:
SJH was supported by a University of Wisconsin CIBM fellowship (5T15LM007359-14). We acknowledge
support from NIH R01 AG040396 (VS), NIH R01 AG027161 (SCJ), NIH R01 AG37639 (BBB), NSF CCF
1320755 (VS), NSF CAREER award 1252725 (VS), UW ADRC AG033514, UW ICTR 1UL1RR025011,
Waisman Core grant P30 HD003352-45 and UW CPCP AI117924.





