Quadratic integer programming approach for MRF-based labeling problems (Master's Thesis)
Abstract. Many low-level vision problems can be formulated as discrete value assigning problems.
In order to find the most plausible labels for each problem, their underlying objectives are defined as energy minimization problems that consider both individual measurement and second order congruency.
Once constructed as graphical models such as Markov Random Field (MRF) and factor graphs, the problems become applicable to many state-of-the-art inference methods that are largely categorized as message passing and move making techniques.
However, the versatilities of the methods are bounded by the characteristics of the function.
We present a quadratic integer programming (QIP) approach to solve MRF based low-level vision problems.
With auxiliary penalty and smoothness terms, the QIP is indiscriminative of functions such that it is capable of converging to the global optimum regardless of the curvature of the Hessian matrix originated from the problem.
Also, using truncated Newton method with preconditioned conjugate gradient descent direction, the convergence is robust and efficient. Based on OpenGM framework, we thoroughly analyze the strengths and weaknesses of the QIP with many state-of-the-art inference methods and demonstrate its potential as the stepping stone to a new approach to solve low-level vision problems.
Figure: Examples of dtf-chinesechar results. Top row: Given images of Chinese letters with missing portions. Bottom row: QIP results of the respective top images.
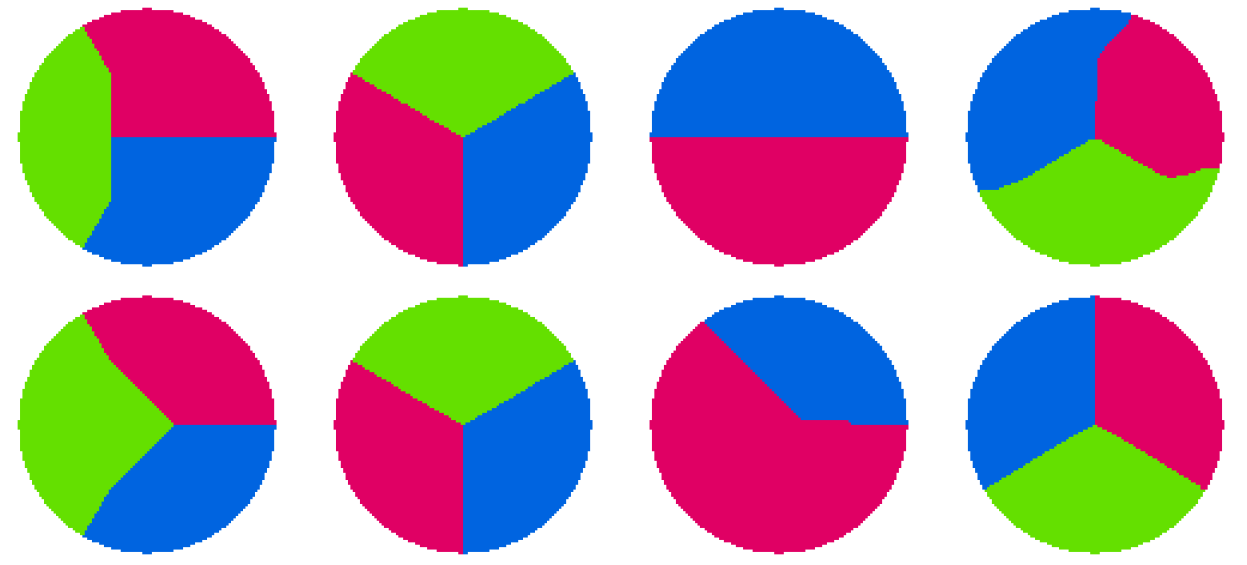Figure: Examples of inpainting-n4 and inpainting-n8 results. Top row: inpainting-n4 results. From left to right: TRWS-LF2 and QIP for plain ring, TRWS-LF2 and QIP for inverse ring. Bot-tom row: inpainting-n8 results. From left to right: TRWS-LF2 and QIP for plain ring, TRWS-LF2 and QIP for inverse ring.
Figure: Examples of color-seg-n4 results. Left column: TRWS-LF2. Right column: QIP
Figure: Examples of mrf-stereo results. Top: ground truth disparity map. Bottom: QIP results disparity map.
References:
[1] Seong Jae Hwang, "Quadratic integer programming approach for MRF-based labeling problems",
Master's Thesis, 2013.
[pdf]
[2] B. Andres, T. Beier, and J. H. Kappes. OpenGM: A C++ Library for Discrete Graphical Models. ArXiv e-prints, 2012.