Introduction to Trees

Contents

• Introduction: Trees and Binary Trees

Introduction

Lists, stacks, and queues are all linear structures: in all three data structures, one item follows another. Trees will be our first non-linear structure:

• More than one item can follow another.
• The number of items that follow can vary from one item to another.

Trees have many uses:

• representing family genealogies
• as the underlying structure in decision-making algorithms
• to represent priority queues (a special kind of tree called a heap)
• to provide fast access to information in a database (a special kind of tree called a b-tree)

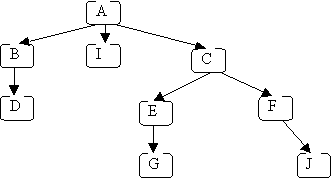
Here is the conceptual picture of a tree (of letters):

• each letter represents one node
• the arrows from one node to another are called edges
• the topmost node (with no incoming edges) is the root (node A)
• the bottom nodes (with no outgoing edges) are the leaves (nodes D, I, G & J)

So a (computer science) tree is kind of like an upside-down real tree.

A path in a tree is a sequence of (zero or more) connected nodes; for example, here are 3 of the paths in the tree shown above:

The length of a path is the number of nodes in the path, e.g.:

The height of a tree is the length of the longest path from the root to a leaf; for the above example, the height is 4 (because the longest path from the root to a leaf is A → C → E → G, or A → C → E → J). An empty tree has height = 0.

The depth of a node is the length of the path from the root to that node; for the above example:

• the depth of J is 4
• the depth of D is 3
• the depth of A is 1

Given two connected nodes like this:

Node A is called the parent, and node B is called the child.

A subtree of a given node includes one of its children and all of that child's descendants. The descendants of a node N are all nodes reachable from N (N's children, its children's children, etc.). In the original example, node A has three subtrees:

1. B, D
2. I
3. C, E, F, G, J

An important special kind of tree is the binary tree. In a binary tree:

• Each node has 0, 1, or 2 children.
• Each child is either a left child or a right child.

Here are two examples of binary trees that are different:

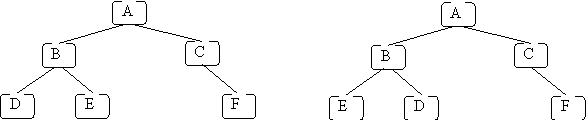
The two trees are different because the children of node B are different: in the first tree, B's left child is D and its right child is E; in the second tree, B's left child is E and its right child is D. Also note that lines are used instead of arrows. We sometimes do this because it is clear that the edge goes from the higher node to the lower node.

Next: Continue with Priority Queues