Heaps and Priority Queues

Contents

• Introduction
• Inserting into a Heap
• Removing from a Heap
• Heap Implementation

Introduction

A heap is a way to implement a priority queue.

The property of a priority queue is:

• when you get an item it is the one with the highest priority

The highest priority item could be:

• the smallest one
• the largest one
• some other method of determining

For these notes the bigger item has a higher priority.

What are some uses for priority queues:

• simulation to order events
• parking assignment at UW. The next person to get a space is the one with the highest priority and not the earliest person to ask (which would be a normal queue).

Why not use an ADT we already know to implement priority queues?

1. BST:

• highest priority item is to the far right. Expected complexity is O(log(n)) but worst case is O(n).
• insert has same complexity.

1. Balanced search tree:

• like BST but complexity is guaranteed to be O(log(n))

Heaps have same complexity as a balanced search tree but:

• they can easily be kept in an array
• they are much simpler than a balanced search tree
• they are cheaper to run in practice

A heap is a binary tree that has special structure compared to a general binary tree:

1. The root is greater than any value in a subtree

• this means the highest priority is at the root
• this is less information than a BST and this is why it can be easier and faster

• the height is always log(n) so all operations are O(log(n))

Complete binary tree: parents of all but leaf nodes have 2 children. Leaves can differ in depth by 1 but the smaller depth leaves must be on the right part of the binary tree. The nodes on the bottom level fill from left to right.

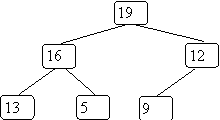
The example from BST as a heap could be:

As with a BST, the location in the heap is not unique. This is a heap with the same values:

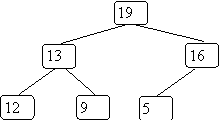
This isn't a heap since it is not complete

Inserting into a Heap

If the binary tree is to be complete, some item must wind up in the next location. To begin we place the new item there. The problem is it may be in the wrong place so we have to fix this. Overall you get:

1. place new item in next location in complete binary tree
2. compare new item to its parent:

1. if new item smaller then you are done
2. else swap parent and child (which is new item) then repeat step 2.

Step 2. lets the item percolate up to its correct location.

Let's insert 14 into our first example:

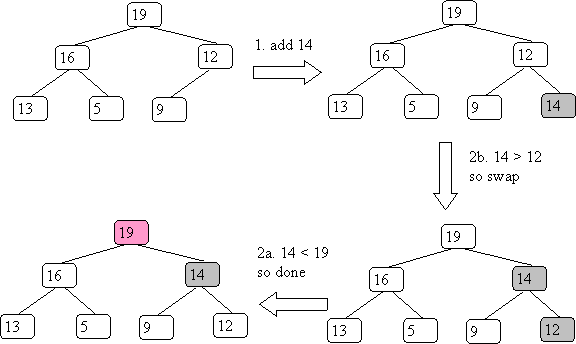
Since the height is log(n), the complexity is worst case O(log(n)). It has been shown that on average you only shift the inserted value 1.6 locations up. Thus, it is O(1) in practice.

Removing from a Heap

Finding the item to remove is easy - it is the root of the tree.

Removing this item destroys the heap structure.

As with insert, we begin by maintaining the complete binary tree structure. Next we fix up the ordering rule for a heap.

The steps are:

1. return the item at the root of the heap
2. remove the last item from the heap (bottom right) and put it at the root.
3. compare the parent to largest child

1. if parent larger you are done
2. else swap parent (which is new item) and larger child then repeat step 3.

Step 3. lets the item percolate down to its correct location.

Continuing our example:

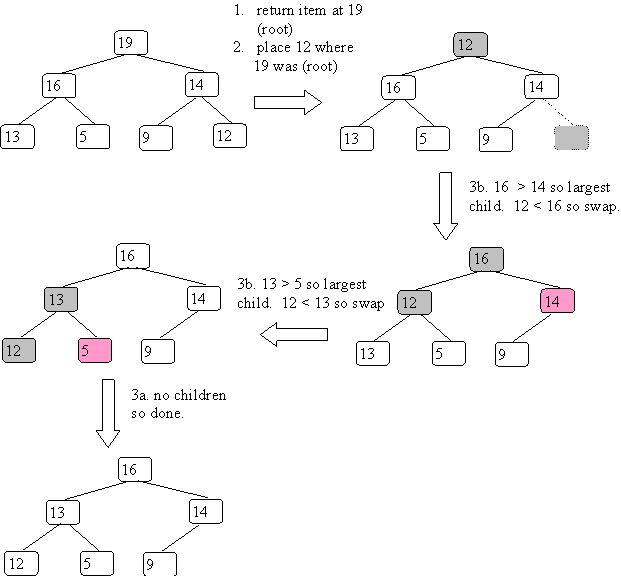
Since the height is log(n), the complexity is O(log(n)). Since you take a value from the bottom, which is small, you generally have to do all log(n) steps.

Heap Implementation

When we talked about general trees, we saw two ways to store them:

1. each node had a linked list of references to the children
2. each node had an array of references to the children

We needed this generality because the number of children varied.

For a complete binary tree we can easily use an array since you must have 2 children of every node except for leaves and these must at the bottom of the tree.

The storage scheme is simple: you put them in the array starting at index 0 as they occur in a level-order traversal.

Our previous example is:

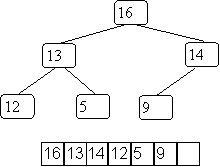
A good question is how do you know what size array to use?

If you know the number of nodes then create an array of that size.

If you don't know the exact number you will have but have an idea of the maximum height you can use:

• The maximum number of nodes is 2^h - 1 where h is the height of the tree. Recall 2^x is the inverse of log₂(x).

If the tree grows beyond this you can resize it.

How can you get the tree structure from the array location?

• if the parent is at index p

• left child is at index 2p+1

• right child is at index 2p+2

You can tell if the child does not exist by:

• noting that the child index is larger than the last array index

To do the inverse operation:

• if the child is at index c

• the parent is at index (c-1)/2 [with truncation]

In our example:

• parent 13 is at index 1
• left child 12 is at index 3 = 2 * 1 + 1
• right child 5 is at index 4 = 2 * 1 + 2
• The right child of 14 at index 2 is at index 6 that is empty so it has no right child.
• The left child of 12 at index 3 is at index 7 that is off the end of the array so no left child.
• child 14 is at index 2
• parent 16 is at index 0 = (2 - 1) / 2

The root that has the maximum priority is at index 0.

Why not use this for a general binary tree?

You can have "missing children" in a general binary tree. These represent empty locations (null references) in the array. Using a linked representation can cut down on this (you only need the first null child). Which is better depends on how full the binary tree is.