Priority Queues

Contents

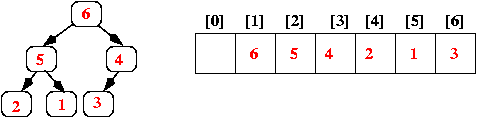
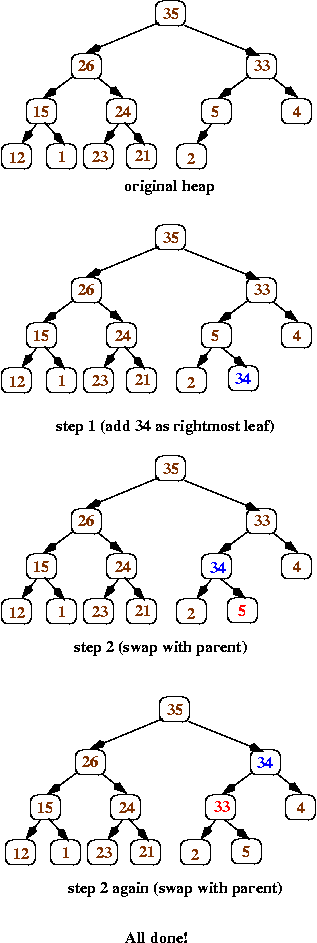
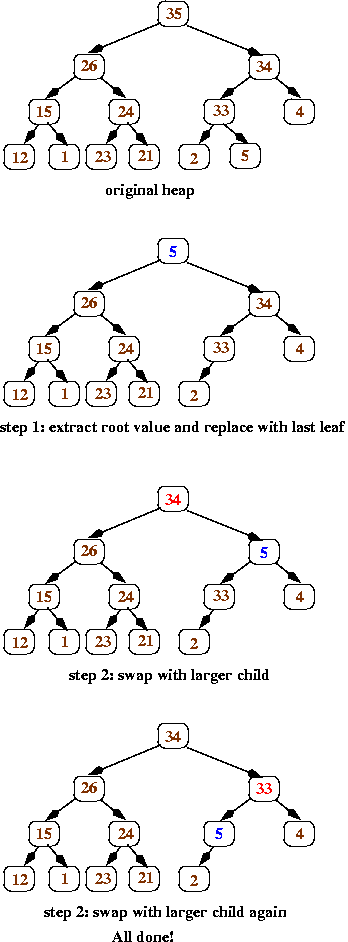
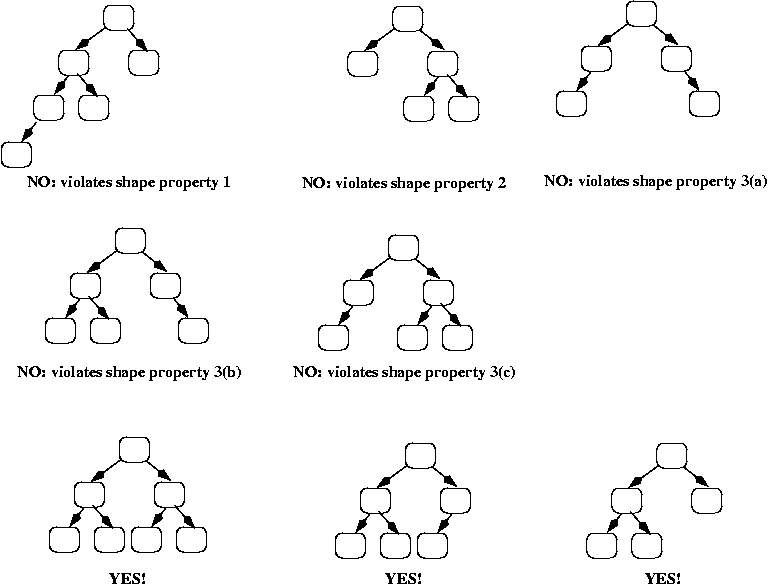Introduction

Here is a conceptual picture of a priority queue:

Think of a priority queue as a kind of bag that holds priorities. You can put one in, and you can take out the current highest priority. (Priorities can be any Comparable values; in our examples, we'll just use numbers.)

A priority queue is different from a "normal" queue, because instead of being a "first-in-first-out" data structure, values come out in order by priority. A priority queue might be used, for example, to handle the jobs sent to the Computer Science Department's printer: Jobs sent by the department chair should be printed first, then jobs sent by professors, then those sent by graduate students, and finally those sent by undergraduates. The values put into the priority queue would be the priority of the sender (e.g., using 4 for the chair, 3 for professors, 2 for grad students, and 1 for undergrads), and the associated information would be the document to print. Each time the printer is free, the job with the highest priority would be removed from the print queue, and printed. (Note that it is OK to have multiple jobs with the same priority; if there is more than one job with the same highest priority when the printer is free, then any one of them can be selected.)

The operations that need to be provided for a priority queue are shown in the following table, assuming that just priorities (no associated information) are to be stored in a priority queue.

OPERATION DESCRIPTION
PriorityQ() (constructor) create an empty priority queue
boolean empty() return true iff the priority queue is empty
void insert(Comparable p) add priority p to the priority queue
Comparable removeMax() remove and return the highest priority from the priority queue (error if the priority queue is empty)

A priority queue can be implemented using many of the data structures that we've already studied (an array, a linked list, or a binary search tree). However, those data structures do not provide the most efficient operations. To make all of the operations very efficient, we'll use a new data structure called a heap.

TEST YOURSELF #1

Consider implementing a priority queue using an array, a linked list, or a BST. For each, describe how each of the priority queue operations would be implemented, and what the worst-case time would be.

solution

Heaps

A heap is a binary tree (in which each node contains a Comparable key value), with two special properties:

The ORDER property:

The SHAPE property:

  1. All leaves are either at depth d or d-1 (for some value d).
  2. All of the leaves at depth d-1 are to the right of the leaves at depth d.
  3. (a) There is at most 1 node with just 1 child. (b) That child is the left child of its parent, and (c) it is the rightmost leaf at depth d.
Here are some binary trees, some of which violate the shape properties, and some of which respect those properties:

And here are some more trees; they all have the shape property, but some violate the order property:

Implementing priority queues using heaps

Now let's consider how to implement priority queues using a heap. The standard approach is to use an array (or an ArrayList), starting at position 1 (instead of 0), where each item in the array corresponds to one node in the heap:

Here's an example, showing both the conceptual heap (the binary tree), and its array representation:

Note that the heap's "shape" property guarantees that there are never any "holes" in the array.

The operations that create an empty heap and return the size of the heap are quite straightforward; below we discuss the insert and removeMax operations.

Implementing insert

When a new value is inserted into a priority queue, we need to:

The way to achieve these goals is as follows:
  1. Add the new value at the end of the array; that corresponds to adding it as a new rightmost leaf in the tree (or, if the tree was a complete binary tree, i.e., all leaves were at the same depth d, then that corresponds to adding a new leaf at depth d+1).
  2. Step 1 above ensures that the heap still has the shape property; however, it may not have the order property. We can check that by comparing the new value to the value in its parent. If the parent is smaller, we swap the values, and we continue this check-and-swap procedure up the tree until we find that the order property holds, or we get to the root.
Here's a series of pictures to illustrate inserting the value 34 into a heap:

TEST YOURSELF #2

Insert the values 6, 40, and 28 into the tree shown above (after 34 has been inserted).

solution

Implementing removeMax

Because heaps have the order property, the largest value is always at the root. Therefore, the removeMax operation will always remove and return the root value; the question then is how to replace the root node so that the heap still has the order and shape properties.

The answer is to use the following algorithm:

  1. Replace the value in the root with the value at the end of the array (which corresponds to the heap's rightmost leaf at depth d). Remove that leaf from the tree.
  2. Now work your way down the tree, swapping values to restore the order property: each time, if the value in the current node is less than one of its children, then swap its value with the larger child (that ensures that the new root value is larger than both of its children).
Here's a series of pictures to illustrate the removeMax operation applied to the heap shown above.

TEST YOURSELF #3

Perform 3 more removeMax operations using the example tree.

solution

Complexity

For the insert operation, we start by adding a value to the end of the array (constant time, assuming the array doesn't have to be expanded); then we swap values up the tree until the order property has been restored. In the worst case, we follow a path all the way from a leaf to the root (i.e., the work we do is proportional to the height of the tree). Because a heap is a balanced binary tree, the height of the tree is O(log N), where N is the number of values stored in the tree.

The removeMax operation is similar: in the worst case, we follow a path down the tree from the root to a leaf. Again, the worst-case time is O(log N).

Summary

A priority queue is a data structure that stores priorities (comparable values) and perhaps associated information. A priority queue supports inserting new priorities, and removing/retrning the highest priority. When a priority queue is implemented using a heap, the worst-case times for both insert and removeMax are logarithmic in the number of values in the priority queue.