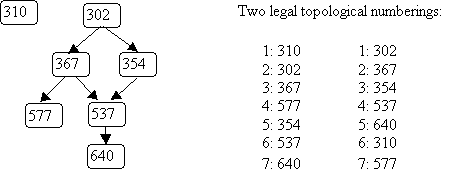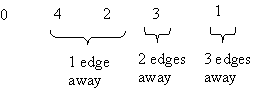Breadth-first Search
Breadth-first search provides another "orderly" way to visit
(part of) a graph.
The basic idea is to visit all nodes at the same distance from the start
node before visiting farther-away nodes.
Like depth-first search, breadth-first search can be used to find all
nodes reachable from the start node.
It can also be used to find the shortest path between two nodes in an
unweighted graph.
Breadth-first search uses a queue rather than recursion (which
actually uses a stack);
the queue holds "nodes to be visited".
If the graph is a tree, breadth-first search gives you a level-order
traversal.
Here's the pseudo code:
static void bfs (Graphnode n) {
Queue Q = new Queue();
n.setVisited( true );
Q.enqueue( n );
while (! Q.empty())){
Graphnode current = (Graphnode)Q.dequeue();
Iterator it = current.getSuccessors().iterator();
while (it.hasNext()) {
Graphnode k = (Graphnode)it.next();
if (! k.getVisited()){
k.setVisited( true );
Q.enqueue( k );
} // end if k not visited
} // end for every successor k
} // end while Q not empty
}
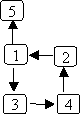
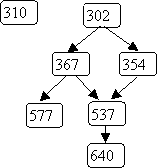
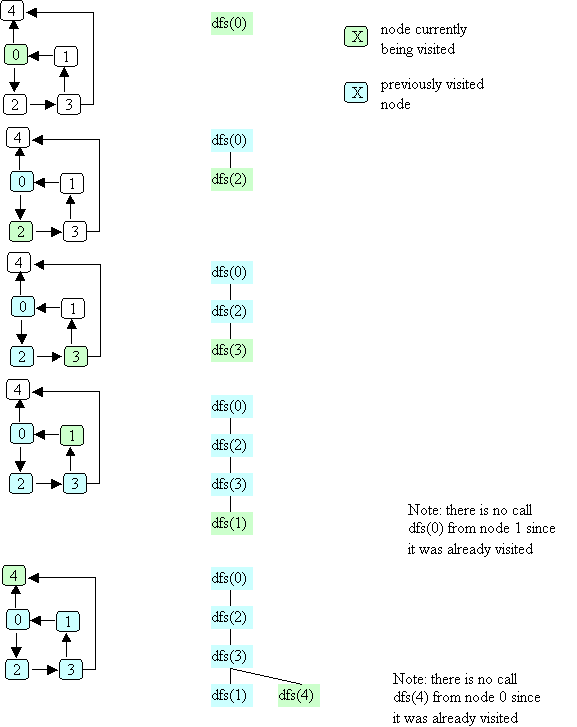
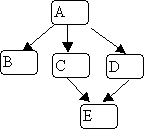
Here's the same example graph we used for depth-first search,
and an illustration of breadth-first search, starting with node 0:
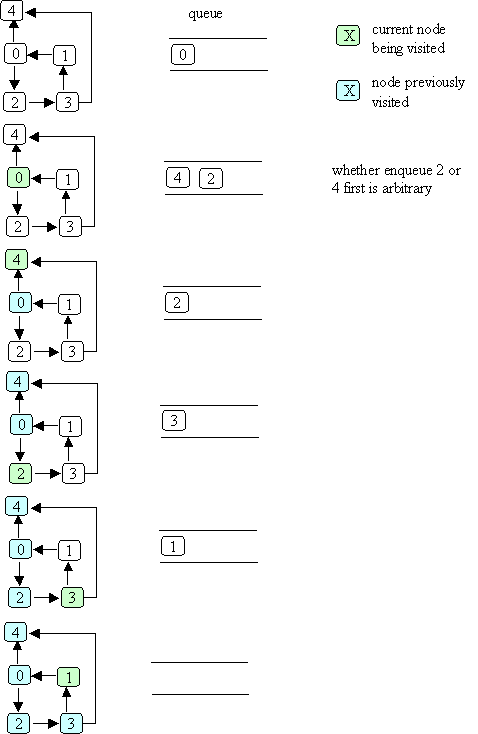
The order in which nodes are "visited" as a result of bfs(0) is:
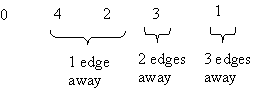
As with depth-first search, all nodes marked "visited" are reachable
from the start node, but nodes are visited in a different order than
they would be using depth-first search.
We can use a variation of bfs to find the shortest distance (the length of
the shortest path) to each reachable node:
- add a "distance" field to each node
- when bfs is called with node n, set n's distance to zero
- when a node k is about to be enqueued, set k's distance to the
distance of the current node (the one that was just dequeued) + 1
This technique only works in unweighted graphs (i.e., in graphs
in which all edges are assumed to have length 1).
An interesting problem is how to find shortest paths in a weighted graph;
i.e., given a "start" node n, to find, for each other node m, the
path from n to m for which the sum of the weights on the
edges is minimal (assuming that no edge has a negative weight).
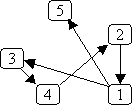
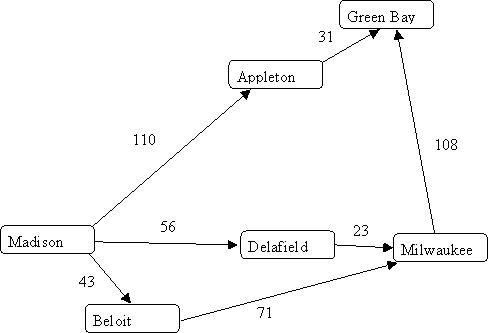
For example, in the following graph, nodes represent cities, edges represent
highways, and the weights on the edges represent distances (the length of
the highway between the two cities).
Breadth-first search can only tell you which route from Madison to
Green Bay goes through the fewest other cities; it cannot tell you
which route is the shortest.
A clever algorithm that can be used to solve this problem (to find
shortest paths in a weighted graph with non-negative edge weights)
has been defined by Edsgar Dijkstra (and so is called "Dijkstra's algorithm").
The worst-case running time of the algorithm is O(E log N), where E
is the number of edges and N is the number of nodes.
You can find a description of the algorithm in most data structures or
algorithms textbooks; you are not responsible for understanding it for this class.
Addition: Since we covered this algorithm in lecture
you are responsible for understanding it.
SUMMARY
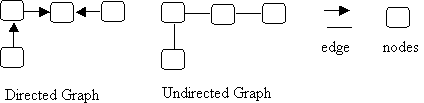
- A graph is a set of nodes and a set of edges.
`
- There are two kinds of graphs: directed and undirected.
- High-level operations include:
- depth-first search,
which can be done on the entire graph (e.g., to find
cycles or to produce a topological ordering), or on part of
a graph (e.g., to determine which nodes are reachable from
a given node)
- breadth-first search, which can also be used to determine
reachability, and can be used to find shortest paths in
unweighted graphs
- Dijkstra's algorithm, which finds shortest paths in weighted graphs.