Implementing Stacks
The stack ADT is very similar to the list ADT; therefore, their implementations are also quite similar.
Both stacks and queues are like lists (ordered collections of items),
but with more restricted operations.
They can both be implemented either using an array or using a linked list
to hold the actual items.
Introduction
| OPERATION | DESCRIPTION |
| Stack() | (constructor) create an empty stack |
| boolean empty() | return true iff the stack is empty |
| int size() | return the number of items in the stack |
| void push(Object ob) | add ob to the top of the stack |
| Object pop() | remove and return the item from the top of the stack (error if the stack is empty) |
| Object peek() | return the item that is on the top of the stack, but do not remove it (error if the stack is empty) |
| OPERATION | DESCRIPTION |
| Queue() | (constructor) create an empty queue |
| boolean empty() | return true iff the queue is empty |
| int size() | return the number of items in the queue |
| void enqueue(Object ob) | add ob to the rear of the queue |
| Object dequeue() | remove and return the item from the front of the queue (error if the queue is empty) |
The stack ADT is very similar to the list ADT;
therefore, their implementations are also quite similar.
Implementing Stacks
| OPERATION | WORST-CASE TIME | AVERAGE-CASE TIME |
| constructor | ||
| empty | ||
| size | ||
| push | ||
| pop | ||
| peek |
To implement a stack using a linked list, we must first define the
Listnode class.
The Listnode definition
is the same one we used for the linked-list implementation of the List class.
The signatures of the methods of the Stack class are independent of
whether the stack is implemented using an array or using a linked list;
only the type of the items field needs to change:
As discussed above, an important property of stacks is that items
are only pushed and popped at one end (the top of the stack).
If we implement a stack using a linked list, we can choose which end of
the list corresponds to the top of the stack.
It is easiest and most efficient to add and remove items at the front
of a linked list,
therefore, we will choose the front of the list as the top of the stack
(i.e., the items field will be a pointer to the node that contains the
top-of-stack item).
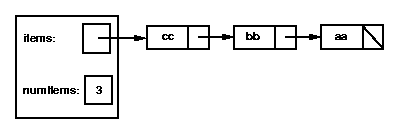
Below is a picture of a stack represented using a linked list; in this
case, items have been pushed in alphabetical order, so "cc" is at the top
of the stack:
Notice that, in the picture, the top of stack is to the left (at the front of
the list), while for the array implementation, the top of stack was to
the right (at the end of the array).
Let's consider how to write the pop method.
It will need to perform the following steps:
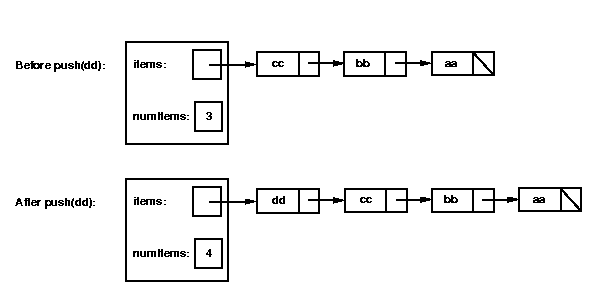
Now let's consider the push method.
Here are before and after pictures, illustrating the effect of a call
to push when the stack is implemented using a linked list:
The steps that need to be performed are:
Complete the push method, using the following header.
Linked-list Implementation
private Listnode items; // pointer to the linked list of items in the stack
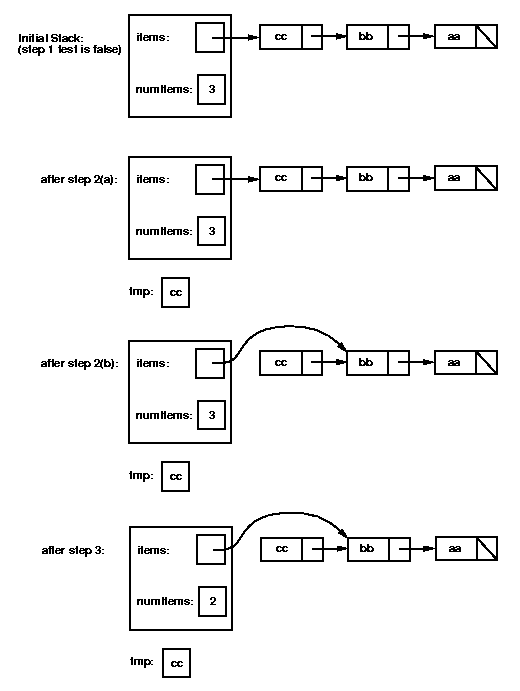
Note that by the time we get to the last step (returning the top-of-stack
value), the first node has already been
removed from the list, so we need to save its value in order to return it
(we'll call that step 2(a)).
Here's the code, and an illustration of what happens when pop
is called for a stack containing "cc", "bb", "aa" (with "cc" at the
top).
public Object pop() throws EmptyStackException {
if (empty()) throw new EmptyStackException(); // step 1
Object tmp = items.getData(); // step 2(a)
items = items.getNext(); // step 2(b)
numItems--; // step 3
return tmp; // step 4
}
public void push(Object ob) {
}
solution
The remaining methods (the constructor, peek, size, and empty) are quite straightforward. You should be able to implement them without any major problems.
Fill in the following table, using Big-O notation to give the worst-case times for each of the stack methods for a stack of size N, assuming a linked-list implementation. Look back at the table you filled in for the array implementation. How do the times compare? What are the advantages and disadvantages of using an array vs using a linked list to implement the Stack class?
| OPERATION | WORST-CASE TIME |
| constructor | |
| empty | |
| size | |
| push | |
| pop | |
| peek |
The main difference between a stack and a queue is that a stack is only
accessed from the top, while a queue is accessed from both ends (from the
rear for adding items, and from the front for removing items).
This makes both the array and the linked-list implementation of a queue
more complicated than the corresponding stack implementations.
Let's first consider a Queue implementation that is very similar to
our (array-based) List implementation.
Here's the class definition:
To make both enqueue and dequeue efficient, we need
the following insight:
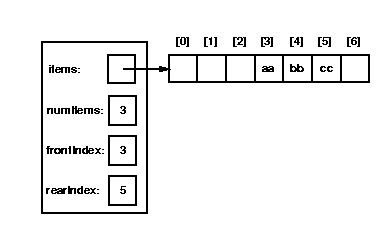
There is no reason to force the front of the queue always to be in items[0],
we can let it "move up" as items are dequeued.
To do this, we need to keep track of the indexes of the items at the
front and rear of the queue (so we need to add two new fields to the
queue class, frontIndex and rearIndex,
both of type int).
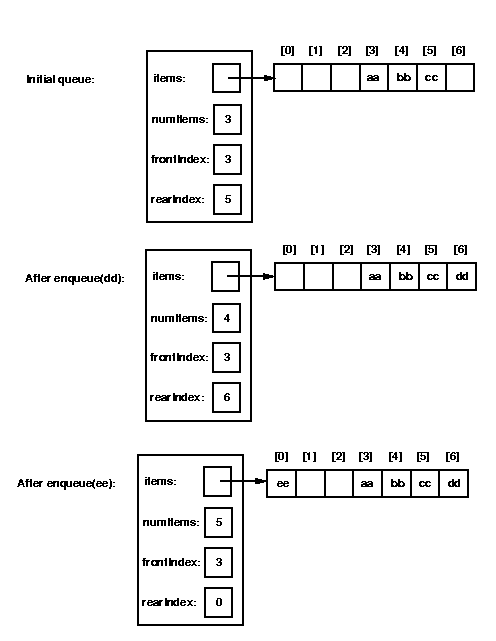
To illustrate this idea, here is a picture of a queue after some
enqueue and dequeue operations have been performed:
Now think about what should happen to this queue if we enqueue two more
items: "dd" and "ee".
Clearly "dd" should be stored in items[6].
Then what?
We could increase the size of the array and put "ee" in items[7], but
that would lead to wasted space -- we would never reuse items[0], items[1],
or items[2].
In general, the items in the queue would keep "sliding" to the right
in the array, causing more and more wasted space at the beginning of
the array.
A better approach is to let the rear index "wrap around" (in this case, from
6 to 0) as long as there is empty space in the front of the array.
Similarly, if after enqueuing "dd" and "ee" we dequeue four items (so
that only "ee" is left in the queue), the front index will have to
wrap around from 6 to 0.
Here's a picture of what happens when we enqueue "dd" and "ee":
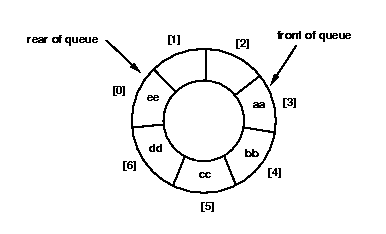
Conceptually, the array is a circular array.
It may be easier to visualize it as a circle.
For example, the array for the final queue shown above could be thought of as:
We still need to think about what should happen if the array is full;
we'll consider that case in a minute.
Here's the code for the enqueue method, with the "full array"
case still to be filled in:
Note that instead of using incrementIndex we could use the mod operator,
and write:
rearIndex = (rearIndex + 1) % items.length.
However, the mod operator is quite slow, and it is easy to get that
expression wrong, so we will use the auxiliary method (with a check
for the "wrap-around" case) instead.
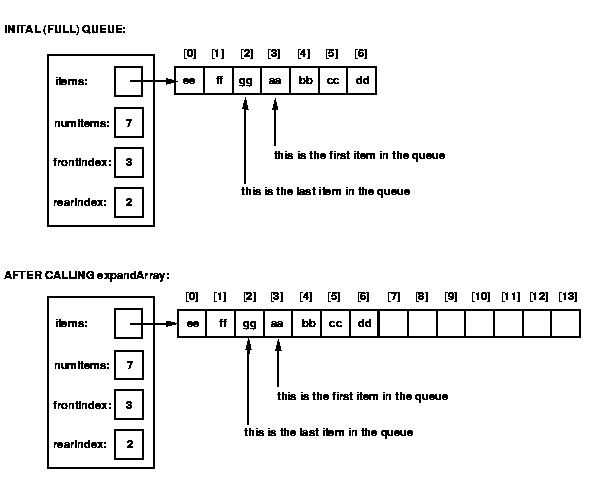
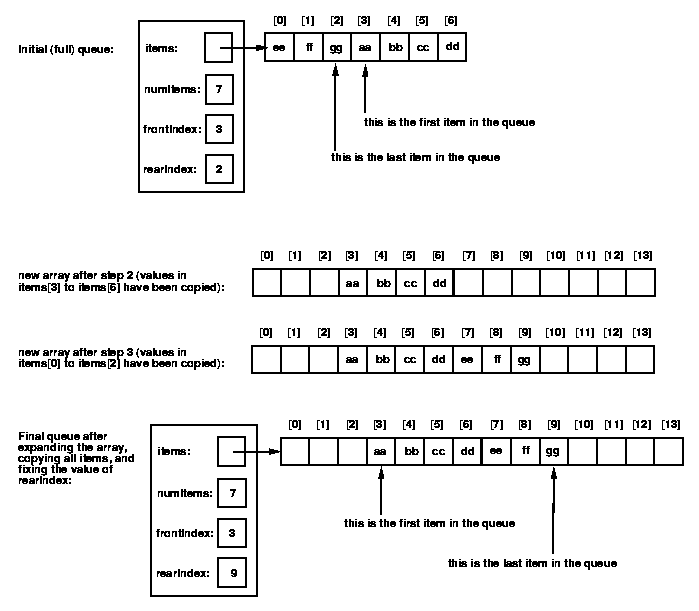
To see why we can't simply use expandArray when the array is full,
consider the picture shown below.
After calling expandArray, the last item in the queue is still right
before the first item -- there is still no place to put the new item
(and there is a big gap in the middle of the queue, from items[7] to
items[13]).
The problem is that expandArray copies the values in the old array into
the same positions in the new array.
This does not work for the queue implementation; we need to move the
"wrapped-around" values to come after the non-wrapped-around values in
the new array.
The steps that need to be carried out when the array is full are:
And here's the final code for enqueue:
The dequeue method will also use method incrementIndex to
add one to frontIndex (with wrap-around) before returning
the value that was at the front of the queue.
The other queue methods (empty and size) are the
same as those methods for the Stack class -- they just use the value
of the numItems field.
The first decision in planning the linked-list implementation of the Queue
class is which end of the list will correspond to the front of the queue.
Recall that items need to be added to the rear of the queue, and removed from
the front of the queue.
Therefore, we should make our choice based on whether it is easier to
add/remove a node from the front/end of a linked list.
If we keep pointers to both the first and last nodes of the list,
we can add a node at either end in constant time.
However, while we can remove the first node in the list in constant time,
removing the last node requires first locating the previous node,
which takes time proportional to the length of the list.
Therefore, we should choose to make the end of the list be the rear of the
queue, and the front of the list be the front of the queue.
The class definition is the same as for the array implementation, except
for the fields:
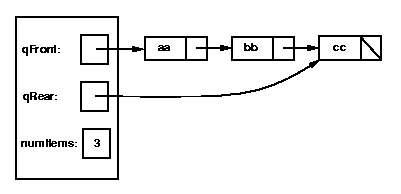
Here's a picture of a Queue with three items, aa, bb, cc, with aa at the
front of the queue:
You should be able to write all of the queue methods, using the code you
wrote for the linked-list implementation of the List class as a guide.
The advantages and disadvantages of the two implementations are essentially
the same as the advantages and disadvantages in the case of the List class:
Implementing Queues
Array Implementation
public class Queue {
// *** fields ***
private static final int INITSIZE = 10; // initial array size
private Object[] items; // the items in the queue
private int numItems; // the number of items in the queue
//*** methods ***
// constructor
public Queue() { ... }
// add items
public void enqueue(Object ob) { ... }
// remove items
public Object dequeue() throws EmptyQueueException { ... }
// other methods
public int size() { ... }
public boolean empty() { ... }
}
We could implement enqueue by adding the new item at the end
of the array and implement dequeue by saving the first item
in the array, moving all other items one place to the left, and
returning the saved value.
The problem with this approach is that, although the enqueue
operation is efficient, the dequeue operation is not -- it requires
time proportional to the number of items in the queue.
public void enqueue(Object ob) {
// check for full array and expand if necessary
if (items.length == numItems) {
// code missing here
}
// use auxiliary method to increment rear index with wraparound
rearIndex = incrementIndex(rearIndex);
// insert new item at rear of queue
items[rearIndex] = ob;
numItems++;
}
private int incrementIndex(int index) {
if (index == items.length-1) return 0;
else return index + 1;
}
Here's an illustration:
publc void enqueue(Object ob) {
// check for full array and expand if necessary
if (items.length == numItems) {
Object[] tmp = new Object[items.length*2];
System.arraycopy(items, frontIndex, tmp, frontIndex,
items.length-frontIndex);
if (frontIndex != 0) {
System.arraycopy(items, 0, tmp, items.length, frontIndex);
}
items = tmp;
rearIndex = frontIndex + numItems - 1;
}
// use auxiliary method to increment rear index with wraparound
rearIndex = incrementIndex(rearIndex);
// insert new item at rear of queue
items[rearIndex] = ob;
numItems++;
}
Linked-list Implementation
// *** fields ***
private Listnode qFront; // pointer to the front of the queue
// (the first node in the list)
private Listnode qRear; // pointer to the rear of the queue
// (the last node in the list)
private int numItems; // the number of items in the queue
Comparison of Array and Linked-List Implementations