Introduction
Recursion is:
- A way of thinking about problems.
- A method for solving problems.
- Related to mathematical induction.
void f() {
... f() ...
}
or indirectly:
void f() {
... g() ...
}
void g() {
... f() ...
}
You might wonder about the following issues:
-
Q: Does using recursion usually make your code faster?
A: No.
Q: Does using recursion usually use less memory?
A: No.
Q: Then why use recursion?
A: It sometimes makes your code much simpler!
One way to think about recursion:
- When a recursive call is made, the method clones itself,
making new copies of:
- the code
- the local variables (with their initial values),
- the parameters
- Each copy of the code includes a marker indicating the current position. When a recursive call is made, the marker in the old copy of the code is just after the call; the marker in the "cloned" copy is at the beginning of the method.
- When the method returns, that clone goes away, but the previous ones are still there, and know what to execute next because their current position in the code was saved (indicated by the marker).
Here's an example of a simple recursive method:
void printInt( int k ) {
1. if (k == 0) {
2. return;
3. }
4. System.out.println( k );
5. printInt( k - 1 );
6. System.out.println("all done");
}
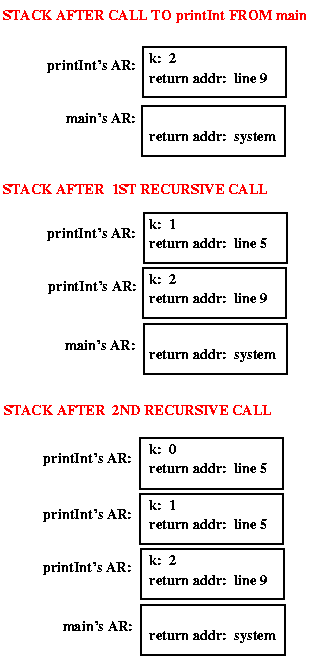
If the call printInt(2) is made, three "clones" are created, as
illustrated below:

The original call causes 2 to be output, and then a recursive call is made, creating a clone with k == 1. That clone executes line 1: the if condition is false; line 4: prints 1; and line 5: makes another recursive call, creating a clone with k == 0. That clone just returns (goes away) because the "if" condition is true. The previous clone executes line 6 (the line after its "marker") then returns, and similarly for the original clone.
Now let's think about what we have to do to make sure that recursive methods work correctly. First, consider the following recursive method:
void badPrint( int k ) {
System.out.println( k );
badPrint( k + 1 );
}
Note that a runtime error will occur when the call badPrint(2)
is made (in particular, an error message like "java.lang.StackOverflowError"
will be printed, and the program will stop).
This is because there is no code that
prevents the recursive call from being made again and again and ....
and eventually the program runs out of memory (to store all the clones).
This is an example of an infinite recursion.
It inspires:
-
Every recursive method must have a base case -- a condition under
which no recursive call is made -- to prevent infinite recursion.
Here's another example; this version does have a base case, but the call badPrint2(2) will still cause an infinite recursion:
void badPrint2( int k ) {
if (k < 0) return;
System.out.println(k);
badPrint2( k+1 );
}
This inspires:
-
Every recursive method must make progress toward the base case
to prevent infinite recursion.
Consider the method printInt, repeated below.
void printInt( int k ) {
if (k == 0) return;
System.out.println( k );
printInt( k - 1 );
}
Does it obey recursion rules 1 and 2?
Are there calls that will lead to an infinite recursion?
If yes, how could it be fixed?
This is how method calls (recursive and non-recursive) really work:
Example (no recursion):
When the first call to printChar returns, the top activation
record is popped from the stack and the main method begins executing
again at line 8.
After executing the assignment at line 8, a second call to
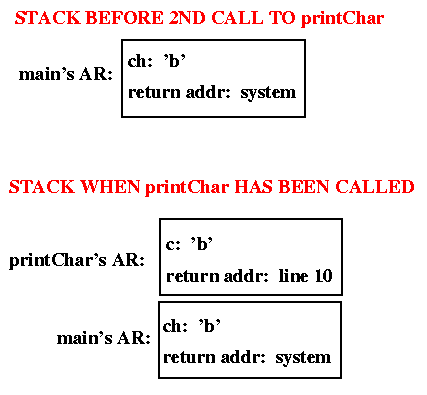
printChar is made (line 9), as illustrated below.
The two calls to printChar return to different places in main
because different return addresses are stored in the ARs that are
pushed onto the stack when the calls are made.
Now let's consider recursive calls:
Note that all of the recursive calls have the same return address -- after
a recursive call returns, the previous call to printInt
starts executing again at line 5.
In this case, there is nothing more to do at that point, so the method would,
in turn, return.
Note also that each call to printInt causes the current value of k to
be printed, so the output of the program is: 2 1.
Now consider a slightly different version of the printInt method:
Now let's think about when it is a good idea to use recursion and why.
In many cases there will be a choice:
many methods can be written either with or without using recursion.
Q: Does the recursive version usually use less memory?
Q: Then why use recursion??
Here are a few examples where recursion makes things a little bit clearer,
though in the second case, the efficiency problem makes it a bad choice.
Factorial can be defined as follows:
The first definition leads to an iterative version of factorial:
Question 1:
Question 2:
Fibonacci can be defined as follows:
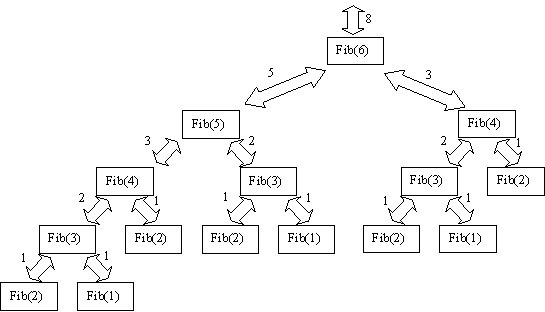
Given that the recursive version of fibonacci is slower than the iterative
version, is there a good reason for using it?
The answer may be yes: because the recursive solution is so much simpler,
it is likely to take much less time to write, debug, and maintain.
If those costs (the cost for programming time) are more important than
the cost of having a slow program, then the advantages of using the
recursive solution outweigh the disadvantage, and you should use it!
If the speed of the final code is of vital importance, then you should
not use the recursive fibonacci.
So far, we've been doing all our recursion based on the value of
some int parameter;
e.g., for factorial, we start with some value N, and each recursive
call passes a smaller value (N - 1) until we get down to 0.
A more common way to use recursion in programming is to base the
recursion on a recursive data structure.
A data structure is recursive if you can define it in terms of
itself.
For example, we can give a recursive definition of a string:
We can give a similar, recursive definition of a linked list:
Below are two methods that use recursive data structures;
the first one prints each
character of its String parameter,
and the second prints each value in its linked-list parameter.
Example 1: Use a String parameter
Example 2: Use a linked-list parameter
Now suppose we want to print the values in a linked list backwards;
i.e., if the list looks like this:
we want to print:
It is easy to do this using recursion;
all we have to do is swap the order of the print statement
and the recursive call in the Example 2 code given above.
Here's the new version:
Question 1:
Question 2:
There are two ways to determine how much time is required for
a call to a recursive method:
To reason about the time required for a call to a recursive method,
you must figure out how many times total the method will be called,
and how much work (in terms of the problem size, N) is done on each
call in addition to the recursive calls.
The total time is the product of those two values.
For example, consider recursive method printInt:
A more formal way to analyze the running time of a recursive method
is to use recurrence equations.
The recurrence equations for a method include an equation for the
base case (or several equations if there are several base cases), and
an equation for the recursive case.
For example, for the printInt method above, the recurrence
equations are:
To find the worst-case time for a problem of size N, we need to find
a closed-form solution to these equations;
i.e., a solution for T(N) that doesn't involve any T(...) on the
right-hand side.
To do that we perform three steps:
Step 1: Expand
Step 2: Look for a pattern and guess a solution
Step 3: Verify the guessed solution
Suppose we have the following recurrence equations:
Finally, verify your solution using the recursive equation.
How Recursion Really Works
1. void printChar( char c ) {
2. System.out.print(c);
3. }
4.
5. void main (...) {
6. char ch = 'a';
7. printChar(ch);
8. ch = 'b';
9. printChar(ch);
10. }
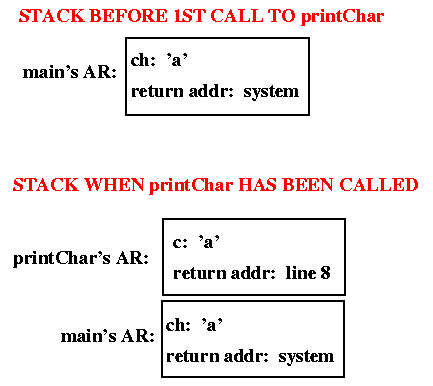
The runtime stack of activation records is shown below, first as it
would be just before the first call to printChar (just after
line 6), and then as it would be while printChar is executing
(lines 1 - 3).
Note that the return address stored in printChar's AR is the
place in main's code where execution will resume when
printChar returns.
1. void printInt( int k ) {
2. if (k <= 0) return;
3. System.out.println( k );
4. printInt( k - 1 );
5. }
6.
7. void main(...) {
8. printInt(2);
9.}
The following pictures illustrate the runtime stack as this program executes.
1. void printInt (int k) {
2. if (k<=0) return;
3. printInt (k-1);
4. System.out.println(k)
5. }
Now what is printed as a result of the call printInt(2)?
Because the print statement comes after the recursive call, it
is not executed until the recursive call finishes (i.e.,
printInt's activation record will have line 4 -- the print
statement -- as its return address, so that line will be executed only
after the recursive call finishes).
In this case, that means that the output is: 1 2 (instead of 2 1, as
it was when the print statement came before the recursive call).
This leads to the following insight:
Sometimes a method has more to do following a recursive call;
it gets done only after the recursive call (and all calls it makes) are
finished.
void printTwoInts( int k ) {
if (k == 0) return;
System.out.println( "From before recursion: " + k );
printTwoInts( k - 1 );
System.out.println( "From after recursion: " + k );
}
What is printed as a result of the call printTwoInts(3)?
Recursion vs Iteration
Q: Is the recursive version usually faster?
A: No -- it's usually slower (due to the overhead of maintaining the stack)
A: No -- it usually uses more memory (for the stack).
A: Sometimes it is much simpler to write the recursive version.
Factorial
or:
(Note that factorial is undefined for negative numbers.)
int factorial (int N) {
if (N == 0) return 1;
int tmp = N;
for (int k=N-1; k>=1; k--) tmp = tmp*k;
return (tmp);
}
The second definition leads to a recursive version:
int factorial (int N) {
if (N == 0) return 1;
else return (N*factorial(N-1));
}
The recursive version is
Because the recursive version causes an activation record to be pushed
onto the runtime stack for every call, it is also more limited than
the iterative version (it will fail, with a "stack overflow" error), for
large values of N.
Draw the runtime stack, showing the activation records that would be
pushed as a result of the call factorial(3) (using the recursive
version of factorial).
Just show the value of N in each AR (don't worry about the return address).
Also indicate the value that is returned as the result of each call.
Recall that (mathematically) factorial is undefined for a negative number.
What happens as a result of the call factorial(-1)
for each of the two versions (iterative and recursive)?
What do you think really should happen when the call factorial(-1) is made?
How could you write the method to make that happen?
Fibonacci
Fibonacci can be programmed either using iteration, or using recursion.
Here are the two versions (iterative first):
// iterative version
int fib (int N) {
int k1, k2, k3;
k1 = k2 = k3 = 1;
for (int j = 3; j <= N; j++) {
k3 = k1 + k2;
k1 = k2;
k2 = k3;
}
return k3;
}
// recursive version
int fib (int N) {
if ((N == 1) || (N == 2)) return 1;
else return (fib (N-1) + fib (N-2));
}
For fibonacci, the recursive version is:
Here's a picture of a "trace" of the recursive version of fibonacci,
for the initial call fib(6):
Recursive Data Structures
A string is either empty, or it is a character followed
by a string.
A linked list is either empty, or it is a list-node followed
by a linked list.
printStr( String S ) {
if (S.equals("")) return;
System.out.print(S.substring(0,1) + " ");
printStr(S.substring(1));
}
printList( Listnode L ) {
if (L == null) return;
System.out.println(L.getData());
printList(L.getNext());
}

itemN
itemN-1
...
item2
item1
printList( Listnode L ) {
if (L == null) return;
printList(L.getNext());
System.out.println(L.getData());
}
In order to print the list backwards without using recursion,
you'd have to use some auxiliary data structure.
For example, you could traverse the list from left to right, pushing
each value into a stack, then pop the stack, printing each value.
However, it's much simpler just to use recursion!
Write a recursive method called sum with the following header:
public static int sum( Listnode L )
Assume that L points to the first node in a linked list of Integers.
Method sum should return the sum of the values in the list.
Write a recursive method called vowels with the following header:
public static String vowels( String S )
Method vowels should return a String containing
just the vowels (a, e, i, o, u) in S, in the order
in which they occur in S.
For example, vowels("hooligan") should return "ooia".
Analyzing Runtime for Recursive Methods
Informal Reasoning
public static void printInt( int k ) {
if (k==0) return;
System.out.println(k);
printInt( k-1 );
}
It is easy to see that if printInt is first called
with the value N, then a total of N+1 calls will be made (for N-1,
N-2, ... 0).
Each time printInt is called, a constant amount of work is done
(to check and print the value of k) in addition to the recursive call.
Therefore, the total time is O(N).
Using Recurrence Equations
T(0) = 1
The first equation says that a problem of size 0 (i.e., when parameter
k == 0), requires a constant amount of work (test k and
return).
The second equation says that a problem of size N (i.e., when parameter
k is not 0), requires a constant amount of work (test and print
k), plus the time required for solving a problem of size N-1.
T(N) = 1 + T(N-1)
Here are those three steps for the printInt equations:
T(0) = 1
T(1) = 1 + T(0) = 1 + 1 = 2
T(2) = 1 + T(1) = 1 + 2 = 3
T(3) = 1 + T(2) = 1 + 3 = 4
We'll guess that T(N) = N+1
T(N) = 1 + T(N-1) // given
N+1 =?= 1 + ((N-1)+1) // replace T(...) on both sides with the guessed solution (N+1) in which each N is replaced by ...
N+1 =?= 1 + N - 1 + 1 // simplify
N+1 = 1 + N // yes the two sides are equal!
T(1) = 1
Do the steps nexcessary to solve those equations.
First, fill in the following table:
T(N) = 1 + 2 * T(N/2)
Next, look for a pattern and guess a solution.
N T(N)
1
2
4
8