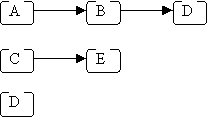
- each letter represents one node
- the arrows from one node to another are called edges
- the topmost node (with no incoming edges) is the root (node A)
- the bottom nodes (with no outgoing edges) are the leaves (nodes D, I, G & J)
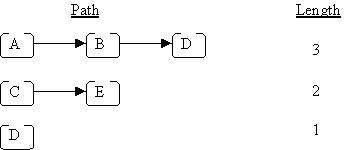
A path in a tree is a sequence of (zero or more) connected nodes; for example, here are 3 of the paths in the tree shown above:
The length of a path is the number of nodes in the path, e.g.:
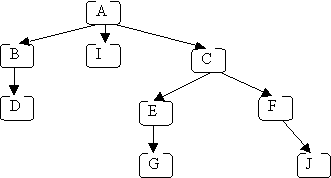
The height of a tree is the length of the longest path from the root to a leaf; for the above example, the height is 4 (because the longest path from the root to a leaf is A → C → E → G, or A → C → E → J). An empty tree has height = 0.
The depth of a node is the length of the path from the root to that node; for the above example:
- the depth of J is 4
- the depth of D is 3
- the depth of A is 1
Given two connected nodes like this:
Node A is called the parent, and node B is called the child.
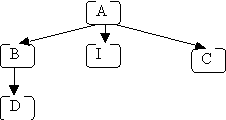
A subtree of a given node includes one of its children and all of that child's descendants. The descendants of a node n are all nodes reachable from n (n's children, its children's children, etc.). In the original example, node A has three subtrees:
- B, D
- I
- C, E, F, G, J.
An important special kind of tree is the binary tree. In a binary tree:
- Each node has 0, 1, or 2 children.
- Each child is either a left child or a right child.
Here are two examples of binary trees that are different:
Since a binary-tree node never has more than two children, a node can
be represented using a class with 3 fields: one for the data in the
node, plus two child pointers:
However, since a general-tree node can have an arbitrary number of
children, a fixed number of child-pointer fields won't work.
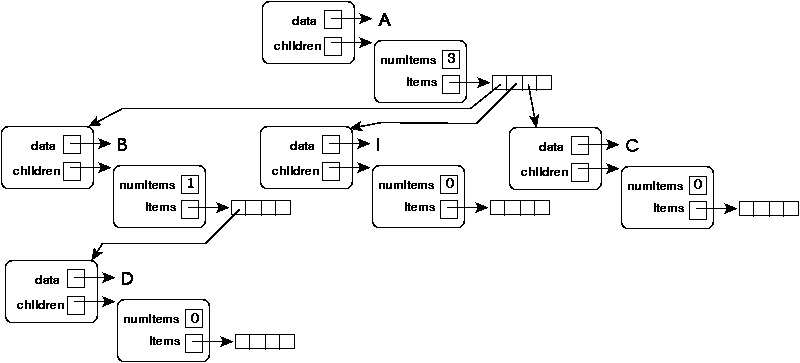
Instead, we can use a List to keep all of the child pointers:
As we know, a list can be represented using either an array or
a linked-list.
For example, consider this general tree (a simplified version of the
original example):
For the array representation of the List (where the array has
an initial size of 4) we would have:
Draw a similar picture of the tree when the List fields are implemented
using linked lists.
It is often useful to iterate through the nodes in a tree:
When we iterated through a List, we started with the first node and
visited each node in turn. Since each node is visited, the best
possible complexity is O(N) for a tree with N nodes. All of our
traversal methods will achieve this complexity.
For trees, there are many different orders in which we might visit the
nodes. There are three common traversal orders for general trees, and
one more for binary trees: preorder, postorder, level order, and
in-order, all described below. We will use the
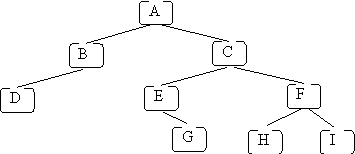
following tree to illustrate each
traversal:
Preorder
A preorder traversal can be defined (recursively) as follows:
If we use a preorder traversal on the example tree given above, and
we print the letter in each node when we visit that node, the
following will be printed: A B D C E G F H I.
Postorder
A postorder traversal is similar to a preorder traversal, except
that the root of each subtree is visited last rather than
first:
If we use a postorder traversal on the example tree given
above, and we print the letter in each node when we visit that node,
the following will be printed: D B G E H I F C A.
Level order
The idea of a level-order traversal is to visit the root, then
visit all nodes "1 level away" (depth 2) from the root (left to
right), then all nodes "2 levels away" (depth 3) from the root,
etc. For the example tree, the goal is to visit the nodes in the
following order:
A level-order traversal requires using a queue (rather than a
recursive algorithm, which implicitly uses a stack). Here's how to
print the data in a tree in level order, using a queue Q, and
using an iterator to access the children of each node
(we assume that the root node is called root, and that
the Treenode class provides a getChildren method):
Draw pictures of Q as it would be each time around the outer while
loop in the code given above for the
example tree given above.
In-order
An in-order traversal involves visiting the root "in between"
visiting its left and right subtrees. Therefore, an in-order traversal
only makes sense for binary trees. The (recursive) definition is:
If we print the letters in the nodes of our example tree using an
in-order traversal, the following will be printed: D B A E G C H F I
The primary difference between the preorder, postorder and in-order
traversals is where the node is visited in relation to the recursive calls;
i.e., before, after or in-between.
What is printed when the following tree is visited using
(a) a preorder traversal, (b) a postorder traversal, (c) a level-order
traversal, and (d) an in-order traversal?
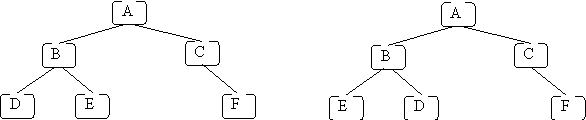
The two trees are different because the children of node B are different:
in the first tree, B's left child is D and its right child is E;
in the second tree, B's left child is E and its right child is D.
Also note that lines are used instead of arrows.
We sometimes do this because it is clear that the edge goes from the higher
node to the lower node.
Representing Trees
class BinaryTreenode {
// *** fields ***
private Object data;
private BinaryTreenode leftChild;
private BinaryTreenode rightChild;
}class Treenode {
// *** fields ***
private Object data;
private List children;
}
(Note that the items in the List will be of type Treenode.)
Tree Traversals
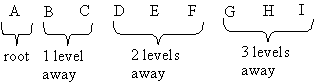
Q.enqueue(root)
while (!Q.empty()) {
Treenode n = Q.dequeue();
System.out.print(n.getData());
List L = n.getChildren();
Iterator it = L.iterator();
while (it.hasNext()) {
Q.enqueue(it.next());
}
}