An important special kind of binary tree is the binary search tree (BST). In a BST, each node stores some information including a unique key value and perhaps some associated data. A binary tree is a BST iff, for every node n, in the tree:
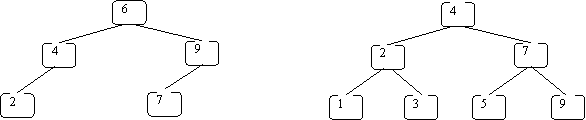
Here are some BSTs in which each node just stores an integer key:

These are not BSTs:
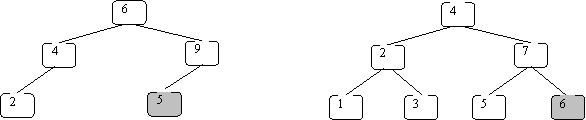
In the left one 5 is not greater than 6. In the right one 6 is not greater than 7.
Note that more than one BST can be used to store the same set of key values. For example, both of the following are BSTs that store the same set of integer keys:

The reason binary-search trees are important is that the following operations can be implemented efficiently using a BST:
TEST YOURSELF #1
Question 1: Which of the following binary trees are BSTs? If a tree is not a BST, say why.
A 10 cat 15
/ \ / / \ / \
B C 5 bat rat 5 22
/ / \ \
-3 ant 20 30
Question 2: Using which kind of traversal (pre-order, post-order, in-order, or level-order) visits the nodes of a BST in sorted order?
To implement a binary search tree, we will use two classes: one for the individual tree nodes, and one for the BST itself. The following class definitions assume that the BST will store only key values, no associated data. Because most of the BST operations require comparing key values, the type used for the key is Comparable (not Object).
class BSTnode {
// *** fields ***
private Comparable key;
private BSTnode left, right;
// *** constructor ***
public BSTnode(Comparable k, BSTnode l, BSTnode r) {
key = k;
left = l;
right = r;
}
// *** methods ***
// accessors (access to fields)
public Comparable getKey() { return key; }
public BSTnode getLeft() { return left; }
public BSTnode getRight() { return right; }
// mutators (change fields)
public void setKey(Comparable k) { key = k; }
public void setLeft(BSTnode l) { left = l; }
public void setRight(BSTnode r) { right = r; }
}
public class BST {
// *** fields ***
private BSTnode root; // ptr to the root of the BST
// *** constructor ***
public BST() { root = null; }
// *** methods ***
public void insert(Comparable key) throws DuplicateException { ... }
// add key to this BST; error if it is already there
public void delete(Comparable key) { ... }
// remove the node containing key from this BST if it is there;
// otherwise, do nothing
public boolean lookup(Comparable key) { ... }
// if key is in this BST, return true; otherwise, return false
public void print(PrintStream p) { ... }
// print the values in this BST in sorted order (to p)
}To implement a BST that stores some data with each key, we would use the following class definitions (changes are in red):
class BSTnode {
// *** fields ***
private Comparable key;
private Object data;
private BSTnode left, right;
// *** constructor ***
public BSTnode(Comparable k, Object d,
BSTnode l, BSTnode r) {
key = k;
data = d;
left = l;
right = r;
}
// *** methods ***
...
public Object getData() { return data; }
public void setData(Object ob) { data = ob; }
...
}
public class BST {
// *** fields ***
private BSTnode root; // ptr to the root of the BST
// *** constructor ***
public BST() { root = null; }
// *** methods ***
public void insert(Comparable key, Object data) throws DuplicateException {...}
// add key and associated data to this BST;
// error if key is already there
public void delete(Comparable key) {...}
// remove the node containing key from this BST if it is there;
// otherwise, do nothing
public Object lookup(Comparable key) {...}
// if key is in this BST, return its associated data; otherwise, return null
public void print(PrintStream p) {...}
// print the values in this BST in sorted order (to p)
}
From now on, we will assume that BSTs only store key values, not
associated data.
We will also assume that null is not a valid key value (i.e., if someone
tries to insert or lookup a null value, that should cause an exception).
The lookup method
In general, to determine whether a given value is in the BST, we will start at the root of the tree and determine whether the value we are looking for:
The code for the lookup method uses an auxiliary, recursive method with the same name (i.e., the lookup method is overloaded):
public boolean lookup(Comparable k) {
return lookup(root, k);
}
private static boolean lookup(BSTnode T, Comparable k) {
if (T == null) return false;
if (T.getKey().equals(k)) return true;
if (k.compareTo(T.getKey()) < 0) {
// k < this node's key; look in left subtree
return lookup(T.getLeft(), k);
}
else {
// k > this node's key; look in right subtree
return lookup(T.getRight(), k);
}
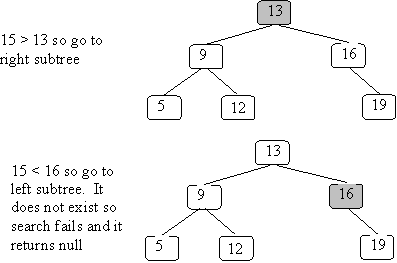
}Let's illustrate what happens using the following BST:
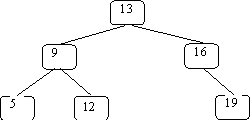
and searching for 12:
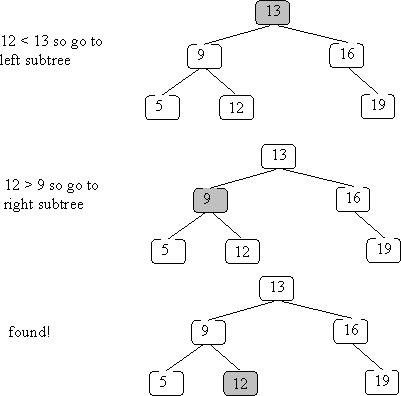
What if we search for 15:
How much time does it take to search for a value in a BST? Note that lookup always follows a path from the root down towards a leaf. In the worst case, it goes all the way to a leaf. Therefore, the worst-case time is proportional to the length of the longest path from the root to a leaf (the height of the tree).
In general, we'd like to know how much time is required for lookup as a function of the number of values stored in the tree. In other words, what is the relationship between the number of nodes in a BST and the height of the tree? This depends on the "shape" of the tree. In the worst case, all nodes have just one child, and the tree is essentially a linked list. For example:
50
/
10
\
15
\
30
/
20
In the best case, all nodes have 2 children and all leaves are at the same depth, for example:
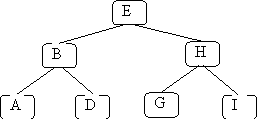
This tree has 7 nodes and height = 3. In general, a tree like this (a "full" tree) will have height approximately log2(N), where N is the number of nodes in the tree. The value log2(N) is (roughly) the number of times you can divide N by two before you get to zero. For example:
7/2 = 3 // divide by 2 once 3/2 = 1 // divide by 2 a second time 1/2 = 0 // divide by 2 a third time, the result is zero so quit
The reason we use log2. (rather than say log3) is because every non-leaf node in a full BST has two children. The number of nodes in each of the root's subtrees is (approximately) 1/2 of the nodes in the whole tree, so the length of a path from the root to a leaf will be the same as the number of times we can divide N (the total number of nodes) by 2.
However, when we use big-O notation, we just say that the height of a full tree with N nodes is O(log N) -- we drop the "2" subscript, because log2(N) is proportional to logk(N) for any constant k, i.e., for any constants B and k and any value N:
To summarize: the worst-case time required to do a lookup in a BST is O(height of tree). In the worst case (a "linear" tree) this is O(N), where N is the number of nodes in the tree. In the best case (a "full" tree) this is O(log N).
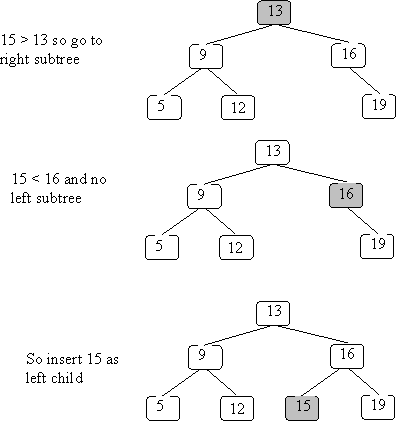
Where should a new item go in a BST? The answer is easy: it needs to go where you would have found it using lookup! If you don't put it there then you won't find it later.
The code for insert is given below. Note that:
public void insert(Comparable k) throws DuplicateException {
if (root == null) {
root = new BSTnode(k, null, null);
}
else insert(root, k);
}
private static void insert(BSTnode T, Comparable k) throws DuplicateException {
// precondition: T != null
if (T.getKey().equals(k))
throw new DuplicateException();
if (k.compareTo(T.getKey()) < 0) {
// add k as left child of T if it doesn't already have one
// else insert into T's left subtree
if (T.getLeft() == null)
T.setLeft( new BSTnode(k, null, null) );
else
insert(T.getLeft(), k);
}
else {
// here when k > T's key
// insert k as right child of T if it doesn't already have one
// else insert into T's right subtree
if (T.getRight() == null)
T.setRight( new BSTnode(k, null, null) );
else
insert(T.getRight(), k);
}
}
It is easy to see that the complexity for insert is the same as for lookup: in the worst case, a path is followed all the way to a leaf.
TEST YOURSELF #2
As mentioned above, the order in which values are inserted determines what BST is built (inserting the same values in different orders can result in different final BSTs). Draw the BST that results from inserting the values 1 to 7 in each of the following orders (reading from left to right):
As you would expect, deleting an item involves a search to locate the node that contains the value to be deleted. Here is an outline of the code for the delete method.
public void delete(Comparable k) {
root = delete(root, k);
}
private static BSTnode delete(BSTnode T, Comparable k) {
if (T == null) return null;
if (k.equals(T.getKey())) {
// T is the node to be removed
// code must be added here
}
else if (k.compareTo(T.getKey()) < 0) {
T.setLeft( delete(T.getLeft(), k) );
return T;
}
else {
T.setRight( delete(T.getRight(), k) );
return T;
}
}There are several things to note about this code:
If the search for the node containing the value to be deleted succeeds, there are three cases to deal with:
When the node to delete is a leaf, we want to remove it from the BST by setting the appropriate child pointer of its parent to null (or by setting root to null if the node to be deleted is the root and it has no children). Note that the call to delete was one of the following:
Here's what happens when the node containing the value 15 is removed from the example BST:

When the node to delete has one child, we can simply replace that node with its child by returning a pointer to that child. As an example, let's delete 16 from the BST just formed:
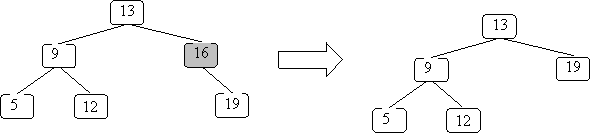
Here's the code for delete, handling the two cases we've discussed so far (the new code is shown in red):
private static BSTnode delete(BSTnode T, Comparable k) {
if (T == null) return null;
if (k.equals(T.getKey())) {
// T is the node to be removed
if (T.getLeft() == null && T.getRight() == null)
return null;
if (T.getLeft() == null)
return T.getRight();
if (T.getRight() == null)
return T.getLeft();
// here if T has 2 children
// code still needs to be added here...
}
else if (k.compareTo(T.getKey()) < 0) {
T.setLeft( delete(T.getLeft(), k) );
return T;
}
else {
T.setRight( delete(T.getRight(), k) );
return T;
}
}The hard case is when the node to delete has two children. We'll call the node to delete n. We can't replace node n with one of its children, because what would we do with the other child? Instead, we will replace node n with another node, x, lower down in the tree, then (recursively) delete node x.
The question is what node can we use to replace node n? We have to choose that node so that the tree is still a BST, i.e., so that all of the values in n's left subtree are less than the value in n, and all of the values in n's right subtree are greater than the value in n. There are two possibilities that work: the node in the left subtree with the largest value or the node in the right subtree with the smallest value. We'll arbitrarily decide to use the node in the right subtree (with the smallest value).
To find that node, we just follow a path in the right subtree, always going to the left child, since smaller values are in left subtrees. Once the node is found, we copy its key into node n, then we recursively delete the copied node. Here's the final version of the delete method:
private static BSTnode delete(BSTnode T, Comparable k) {
if (T == null) return null;
if (k.equals(T.getKey())) {
// T is the node to be removed
if (T.getLeft() == null && T.getRight() == null)
return null;
if (T.getLeft() == null)
return T.getRight();
if (T.getRight() == null)
return T.getLeft();
// here if T has 2 children
BSTnode tmp = smallestNode(T.getRight());
// copy key field from tmp to T
T.setKey( tmp.getKey() );
// now delete tmp from T's right subtree and return
T.setRight( delete(T.getRight(), tmp.getKey()) );
return T;
}
else if (k.compareTo(T.getKey()) < 0) {
T.setLeft( delete(T.getLeft(), k) );
return T;
}
else {
T.setRight( delete(T.getRight(), k) );
return T;
}
}Below is a slightly different example BST; let's see what happens when we delete 13 from that tree.
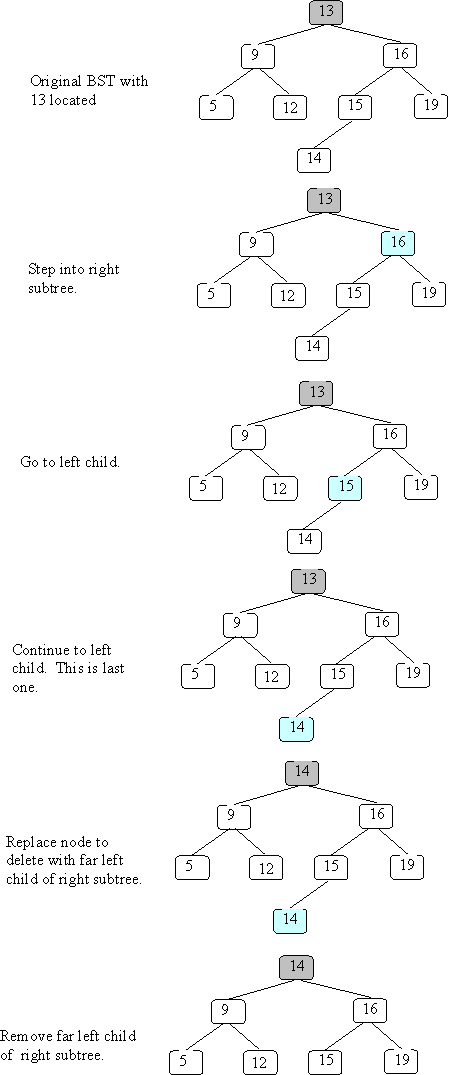
TEST YOURSELF #3
Write the auxiliary method smallestNode used by the delete method given above. The header for smallestNode is:
private static BSTnode smallestNode(BSTnode T) // precondition: T is not null // postcondition: return the node in the subtree rooted at T that // has the smallest value
What is the complexity of the BST delete method?
If the node to be deleted has zero or one child, then the delete method will "follow a path" from the root to that node. So the worst-case time is proportional to the height of the tree (just like for lookup and insert).
If the node to be deleted has two children, the following steps are performed:
Logarithmic time is generally much faster than linear time. For example, for N = 1,000,000: log2 N = 20.
Of course, it is important to remember that for a "linear" tree (one in which every node has one child), the worst-case times for insert, lookup, and delete will be O(N).