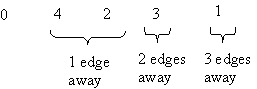Introduction
As discussed in the introduction to graphs notes, graphs are often a good representation for problems involving objects and their relationships because there are standard graph operations that can be used to answer useful questions about those relationships. Here we discuss two such operations: depth-first search and breadth-first search, and some of their applications.
Both depth-first and breadth-first search are "orderly" ways to traverse the nodes and edges of a graph that are reachable from some starting node. The main difference between depth-first and breadth-first search is the order in which nodes are visited. Of course, since in general not all nodes are reachable from all other nodes, the choice of the starting node determines which nodes and edges will be traversed (either by depth-first or breadth-first search).
The basic idea of a depth-first search is to start at some node n, and then
to follow an edge out of n, then another edge out, etc,
getting as far away from n as possible before visiting any more of
n's neighbors.
To prevent infinite loops in graphs with cycles, we must keep track
of which nodes have been visited.
Here is the basic algorithm for a depth-first seach from node n:
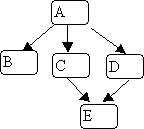
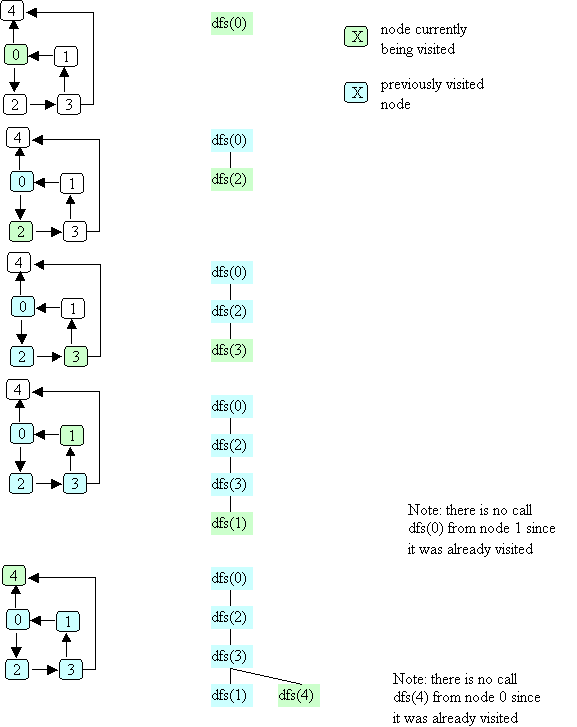
Note that in the example illustrated above, the order in which the nodes
are visited is: 0, 2, 3, 1, 4.
Another possible order (if node 4 were the first successor of node 0) is:
0, 4, 2, 3, 1.
To analyze the time required for depth-first search, note that one call
is made to dfs for each node that is reachable from the start node.
Each call looks at all successors of the current node, so
the time is O(# reachable nodes + total # of outgoing edges from those nodes).
In the worst case, this is all nodes and all edges, so the
worst-case time is O(N + E).
Consider the example given above to illustrate depth-first search.
There is a cycle in that graph starting from
node 0.
Is there something that happens during the depth-first search that
indicates the presence of that cycle??
Note that during dfs(1), 0 is a successor of 1, but is already visited.
But that isn't quite enough to say that there's a cycle, because during
dfs(3), node 4 is a successor of 3 that has already been visited, but there
is no cycle starting from node 4.
What's the difference?
The answer is that when node 0 is considered as a successor of node 1,
the call dfs(0) is still "active" (i.e., its activation record is still
on the stack); however, when node 4 is considered
as a successor of node 3, the call dfs(4) has already finished.
How can we tell the difference??
The answer is to keep track of when a node is "inProgress" (as well as
whether it has been visited or not).
We can do this by using a "mark" field with three possible values:
Here's the code for cycle detection:
Topological numbering addresses exactly this problem.
The goal is to assign numbers to nodes so that for every edge
j -> k, the number assigned to j is less than the number assigned to k.
A topolgoical numbering of the prerequisites graph would tell you
one legal order in which to take the CS courses.
For example:
To find a topological numbering, we use a variation of depth-first search.
The intuition is as follows:
Question 1:
Give two different topological numberings for the following graph.
Question 2:
The topNum method given above only assigns numbers to the nodes reachable
from node n.
Write psuedo code for method numberGraph, similar to the code given for
method graphHasCycle above, that assigns topological
numbers to all nodes in a graph.
Assume that a Graph has a numNodes method that returns the number of nodes
in the graph.
Question 3:
Write a method isConnected, that returns true iff its Graph parameter
is connected.
Again, assume that there is a numNodes method.
Depth-first Search
Depth-first search can be used to answer many questions about a graph:
Information about which nodes have been visited can be kept in
the nodes themselves (e.g., using a boolean field) or in an auxiliary
array of booleans of size N (where N is the number of nodes in the graph).
In both cases, all nodes should be initialized to "unvisited".
Below is code for depth-first search, assuming that visited information
is in a node field named "visited", and that each node's successors
are in a Sequence field named "successors".
Note that this basic depth-first search doesn't actually do anything
except mark nodes as having been visited.
We'll see in the next section how to use variations on this code to
do useful things.
static void dfs (node n) {
n.visited = true;
Sequence S = n.successors;
for (S.start(); S.isCurrent(); S.advance()) {
node m = S.getCurrent();
if (! m.visited) dfs(m);
}
}
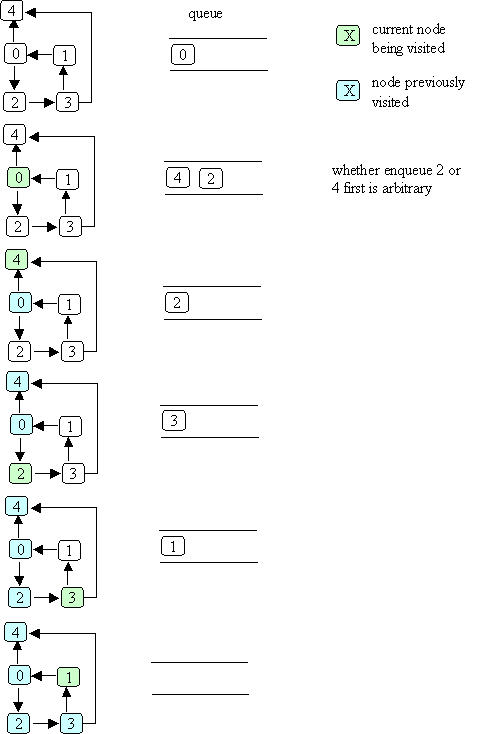
Here's a picture that illustrates the dfs method.
In this example, node numbers are used to denote the nodes themselves
(i.e., the call dfs(0) really means that the dfs method is called with
a pointer to the node labeled 0).
Two different colors are used to indicate the node currently being visited
and the previously visited node.
Uses for Depth-First Search
Recall that at the beginning of this section we said that depth-first
search can be used to answers questions about a graph such as:
Questions 2, 3 and 5 are discussed; the others are left as exercises.
Path Detection
The first question we will consider is: is there a path from node j to node k?
This question might be useful, for example:
To answer the question, do the following:
Cycle Detection
There are two variations that might be interesting:
instead of the boolean "visited" field we've been using.
Initially, all nodes are marked "unvisited".
When the dfs method is first called for node n, it is marked "inProgress".
Once all of its successors have been processed, it is marked "done".
There is a cyclic path reachable from node n iff some node's successor
is found to be marked "inProgress" during dfs(n).
static boolean hasCycle(node n) {
n.mark = inProgress;
Sequence S = n.successors;
for (S.start(); S.isCurrent(); S.advance()) {
node m = S.getCurrent();
if (m.mark == inProgress) return true;
if (m.mark != done) {
if (hasCycle(m)) return true;
}
}
n.mark = done;
return false;
}
Note that if we want to know whether a graph contains a cycle anywhere (not
just one that is reachable from node n) we might have to call
hasCycle at the "top-level" more than once:
static boolean graphHasCycle(Graph G) {
mark all nodes unvisited;
for each node k in the graph {
if (node k is marked unvisited) {
if (hasCycle(k)) return true;
}
}
return false;
}
Topological Numbering
Think again about the graph that represents course prerequisites.
As long as there are no cycles in the graph (which wouldn't make sense,
because it would mean that a course was a prerequisite for itself!)
there is at least one order in which to take courses, such that
all prereqs are satisfied; i.e., so that for every course,
all prerequisites are taken before the course itself is taken.
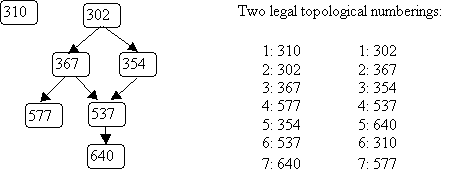
These 2 situations correspond to the point in
method hasCycle where node n is marked "done" (when it has no
more unvisited successors).
We just need to keep track of the current number.
Below is a method that, given a node n and a number num,
assigns topological numbers to all unvisited nodes reachable from n, starting
with num and working down.
Note that before calling this method for the first time, all nodes should
be marked "unvisited", and that the initial call should pass N (the number of
nodes in the graph) as the 2nd parameter.
static int topNum (node n, int num) {
n.mark = inProgress;
Sequence S = n.successors;
for (S.start(); S.isCurrent(); S.advance()) {
node m = S.getCurrent();
if (m.mark == inProgress) {
// no topological ordering for a cyclic graph!
throw new CycleException();
}
if (k.mark != done) num = topNum(k, num);
}
// here when n has no more successors
j.mark = done;
j.number = num;
return num-1;
}
As was the case for cycle detection, we might need several "top-level"
calls to number all nodes in a graph.