• best and expected is O(log(n))
• worst is O(n)

The worst case can happen, for example, when you insert sorted data in a BST.

Potential fixes:

• Periodically (after a certain number of operations) rebalance the tree to make sure height is close to log(n).

• keep the BST balanced so the height is always close to log(n)

The second technique is called balanced trees (possibly more accurate to say balanced search trees). There are many variants:

• AVL: height no worse than log(n) + 1
• red-black: height no worse than 2 * log(n)
• AA
• B-trees: these are not binary trees. They are often used in database where disk access times are a real issue.

We will discuss red-black trees as an example. The details are involved. Keep in mind the important result that the worst case for add, delete and find will be O(log(n)).

An important technique to rebalance the tree is a rotation:

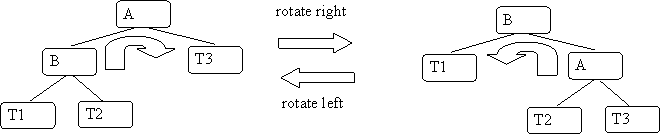
Notice how rotate right makes the right side of the tree higher. Thus, if the height of the left tree is too large then you rotate right. You rotate left for the inverse case.

How do you know you still have a BST? Look at the right rotation and assume you started with a BST on the left:

• On left: B is the left child of A Þ B < A

• On left: T2 is right child of B Þ T2 > B

• On left: T2 is in left subtree of A Þ T2 < A

• T1 and T3 are child of same parent on same side so they are ok

All balanced trees are complex:

• it is hard to see how the rules easily imply a balanced tree
• it is worth using the code of someone else if you can

red-black trees

A BST is a red-black tree if (it also has the standard ordering rules of a BST):

1. every node is either red or black
2. The child of a leaf node is normally null. We make this into a special "null" value where the node has no data but is colored black. (These nodes are just for counting and aren't normally stored in the tree.)
3. If a node is red then both of its children are black. (Note the inverse is not true. A black node can have any color children.)
4. Every path from a node to a descendant leaf contains the same number of black nodes.

It may be hard to see, but these rules imply the height is not worse than 2 * log(n). Here are a few intuitive reasons this is true:

• Rule 4 says that paths have somewhat similar height. The issue is that the number of red nodes isn't included.
• Rule 3 says the number of red nodes in a path is not more than the number of black nodes (Rule 2 guarantees every path ends black to make sure this is true). Combined with rule 4 this implies every path is within a factor of 2 of each other.

Rule 4 is easier to keep track of with this term: black-height of a node is the number of black nodes (not counting itself) from x to all of its leaves (including the null black "node").

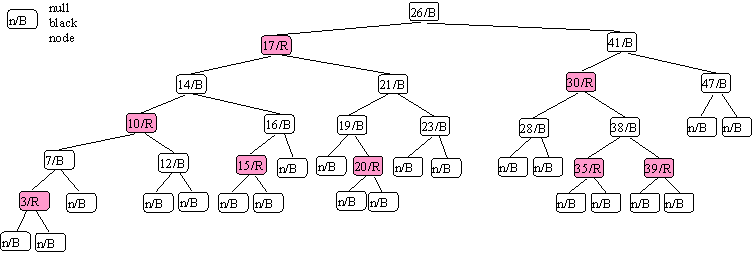
The black-height of 26 (root) is 3

The black-height of 17 is 3

The black-height of 41 is 2

The black-height of whole tree is 4

Insertion into a red-black tree

Here are the basic steps:

1. Apply a BST insert and color the node red.

Note this does not change the black-height so that is still ok

2. Recolor and rotate as necessary to fix up that may have red node with a red child. The cases for this are below. This is what keeps the tree balanced.
3. At very end color the root of the tree black.

Here is some notation:

• X is the offending node and it is red.

• XP is the parent of X. Since X has a problem, XP is also red.
• XGP is the grandparent of X.
• XA is the aunt/uncle of X. This is the other child of XGP. The "A" comes from taking aunt and uncle and combining to get auncle.
• T1, T2, T3, ... are all subtrees with the same black-height and a black root.

There are 6 cases that must be covered in case 2) above:

1. XP (X's parent) is a left child

1. XA (X's auncle) is red
2. XA is black and X is a right child
3. XA is black and X is a left child

1. XP (X's parent) is a right child

1. XA (X's auncle) is red
2. XA is black and X is a left child
3. XA is black and X is a right child

Let's look at the cases:

A.1-3) XP (X's parent) is a left child

A general picture is:

In A.3) X is a left child.

Case A.1) XP (X's parent) is a left child and XA (X's auncle) is red

Here are the steps:

1. color XGP (X 's grandparent) red.

It must have started black because XP is red and it was a red-black tree at the start.

2. color XP (X's parent) and XA (X's auncle) black

Here is what it looks like:

A few points:

• You want to keep the black-height the same. This is done by changing the red nodes one level above X to black and the next level to red. Because of this rules 1, 2, and 4 are preserved.
• You have made the root of this subtree, A, into red. If its parent is red then you have a violation of the rules.
• You apply one of the rules to fix this case.
• Notice the problem node was pushed up toward the root of the whole tree. Once it reaches there (or you don't have a problem) you are done. This is at worst O(log(n)).

• The steps are the same whether X is a left or right child.

Case A.2) XP (X's parent) is a left child and XA (X's auncle) is black and X is a right child

Here are the steps:

1. apply a left rotation to X and XP
2. apply case A.3)

Here is what it looks like:

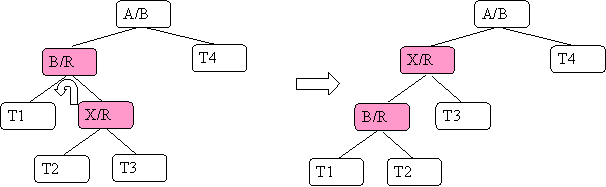
A few points:

• Since we did a left rotation we must take the left child of the original lower node (T2) and make it the right child of the new lower node.
• Since we shifted red nodes we did not change the black-height.
• When you apply A.3) you must think of it this way:

Case A.3) XP (X's parent) is a left child and XA (X's auncle) is black and X is a left child

Here are the steps:

1. reverse the coloring on XP (X's parent) and XGP (X's grandparent)

• note you are doing it in a pair again.

1. apply a right rotation to XP and XGP

Here is what it looks like:

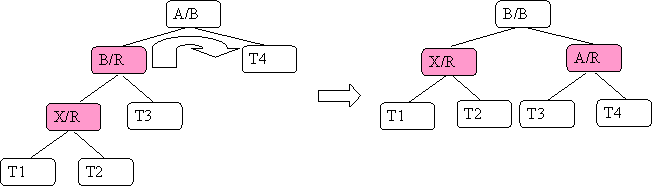
A few points:

• Since we did a right rotation we must take the right child of the original lower node (T3) and make it the left child of the new lower node.
• Since the root is now black the problem does not ripple any farther up the tree.

B.1-3) XP (X's parent) is a right child

As you might expect, the cases are similar to A. but left and right are reversed.

A general picture is:

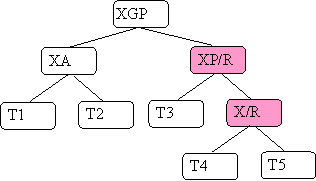
In case B.2) X is a left child.

Case B.1) XP (X's parent) is a right child and XA (X's auncle) is red

Here are the steps:

1. color XGP (X 's grandparent) red.

It must have started black because XP is red and it was a red-black tree at the start.

2. color XP (X's parent) and XA (X's auncle) black

Here is what it looks like:

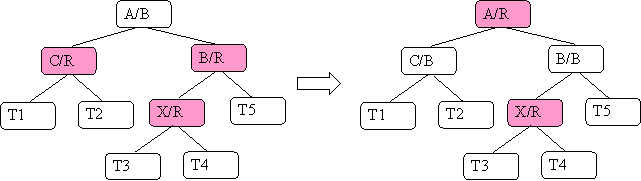
• Once again, the red root of this subtree might need to be fixed.

Case B.2) XP (X's parent) is a right child and XA (X's auncle) is black and X is a left child

Here are the steps:

1. apply a right rotation to X and XP
2. apply case B.3).

Here is what it looks like:

Case B.3) XP (X's parent) is a right child and XA (X's auncle) is black and X is a right child

Here are the steps:

1. reverse the coloring on XP (X's parent) and XGP (X's grandparent)
2. apply a left rotation to XP and XGP

Here is what it looks like:

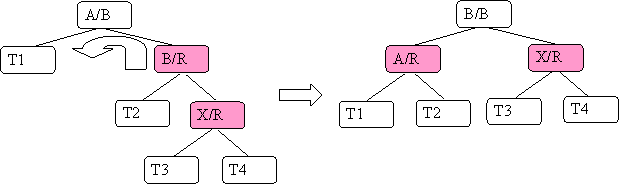
Here are a few examples of insertion:

Red-Black deletion

We will not discuss deletion in detail. However, consider the possibilities:

1. node to delete has no children:



 

S1 is an appropriate subtree so this is a red-black tree at start.

If you delete D and it is black then you change the black-height and this is a problem. Since the node to delete has no children (null black) you don't have a red following red problem.

2. node to delete has 1 child:

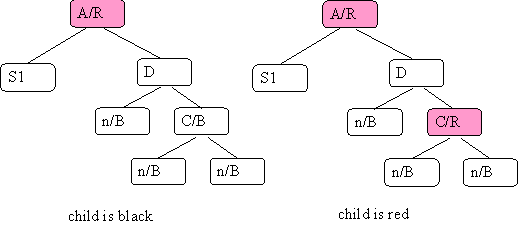
• If the node to delete is black you have a black-height problem as before
• If the parent is red and the child is red then you get a red-red problem

3. node to delete has 2 children:

Here you have more possibilities. Recall you find the smallest successor and replace the deleted node with that.

Note: Weiss makes all null black "nodes" (nB) into same node called null node. This node is black without any element (data value). When doing a search, the code sets the element in null node to key to act as a sentinel. This stops the search from going past the end of the tree.

Quick Highlight

• With a BST you have log(n) £ height £ n
• the expected time for find, add, delete is O(log(n))
• the worst case is O(n)
• With a red-black tree you have log(n) £ height £ 2 * log(n)
• the complexity for find, add, delete is always O(log(n))