The value shown in the tree is the key. It shows the value to use to find an item. There may be other information included with the record associated with the key.General Trees
So far we have mostly looked at the details of ADTs that implement lists:
Both of these structures are linear: one item follows another.
Trees will be our first non-linear structure:
Advantages:
Trees have many uses:
Terminology
Trees have terminology you need to know to discuss them.
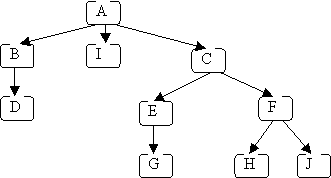
We will use this example of a tree for now:
The value shown in the tree is the key. It shows the value to use to find an item. There may be other information included with the record associated with the key.
All of our trees will have one root
Notice you can define this recursively:
We will use recursion a lot with trees.
Representation
Unlike a linked list, the number of items following a given item can be arbitrary. Thus, using individual fields to store is not practical (like next). Here are other choices:
Let's look at the example where we assume the array is size 4 in every node:
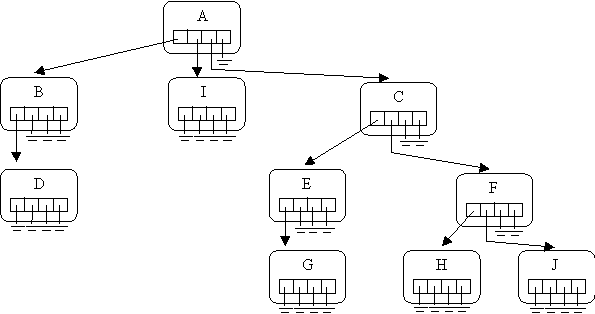
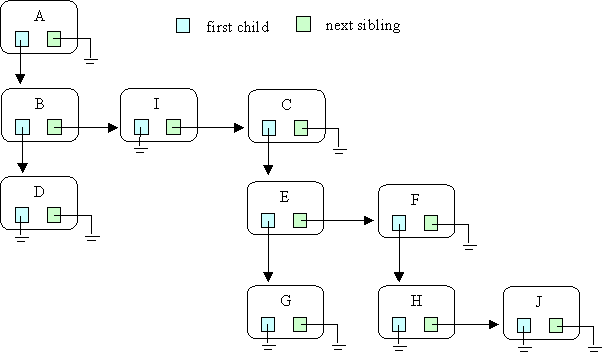Here is the example:
Binary Tree
A binary tree is an important special case of a tree:
The original example is not a binary tree because node A is degree 3.
Here are two examples of binary trees that are different:
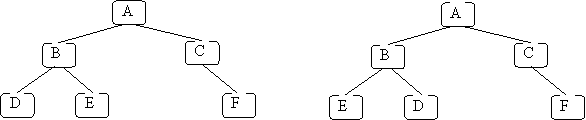The are different because D and E switched places. The left and right child are different.
I have not drawn the edges as arrows. In many places the arrow is implicit from the node higher up to the lower node.
Here are some important special cases:
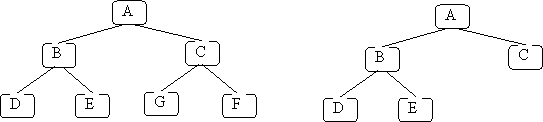The left example is a full binary tree. The right example is not because leaf C is not the same depth as leaves D and E. The two previous examples of binary trees are not full because not all nodes that are not leaves are degree 2.
Traversals
Often one needs to look at every item in a data structure:
Because linked lists were linear, there was one clear choice: go from one item to the next one.
Trees are nonlinear so there are several possible orders that make sense. For a tree this is known as a traversal.
Since you go to every node in the tree, the complexity is at best O(n). All the algorithms we will see achieve this.
You can traverse a general tree but it is more common to talk about it in terms of a binary tree. That is what we will do here.
For a binary tree, the different traversals vary by when you visit the node, its left child and its right child.
The easiest way to view the traversals is with recursion. Section 17.4 of the book shows how to do it without recursion. The code is more complicated but can be faster in some cases. It involves using a stack to mimic the recursion.
Notice you don't need to know how a binary tree ADT works to describe the traversals. The logical operations are independent of the implementation. We will talk about the implementation and storage of a binary tree later.
For these examples, I will use this binary tree:
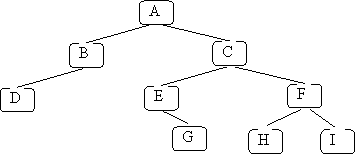
When you visit a node in a traversal you could do any operation you want. In these examples I will print out the data stored at the node. I assume only the key is stored.
It is convention that you visit the left child before the right child in a normal order traversal.
preorder traversal:
Pseudo-code for this would be:
void preorder() {
print data at node
if (there is a left child) {
left_child.preorder ()
}
if (there is a right child) {
right_child.preorder ()
}
}
For the above example the output would be: A B D C E G F H I
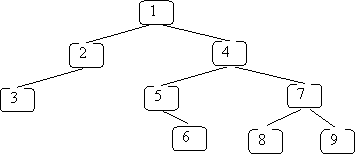
If you replace the key with a number representing the order in which the nodes are visited in a preorder traversal you get:
inorder traversal:
Pseudo-code for this would be:
void inorder() {
if (there is a left child) {
left_child.inorder ()
}
print data at node
if (there is a right child) {
right_child.inorder ()
}
}
For the above example the output would be: D B A E G C H F I
If you replace the key with a number representing the order in which the nodes are visited in an inorder traversal you get:
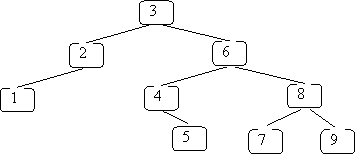
postorder traversal:
Pseudo-code for this would be:
void postorder() {
if (there is a left child) {
left_child.postorder ()
}
if (there is a right child) {
right_child.postorder ()
}
print data at node
}
For the above example the output would be: D B G E H I F C A
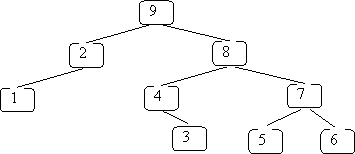If you replace the key with a number representing the order in which the nodes are visited in a postorder traversal you get:
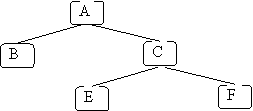All of these traversals are good examples of recursion. To make it shorter, let's use this example:
For the postorder traversal, the call tree looks like:
postorder(A)
postorder(B)
output B
postorder(C)
postorder(E)
output E
postorder(F)
output F
output C
output A
The different traversals are just a matter of what order you do the steps. This is what you do before or after the recursive call. We saw when we studied recursion this makes a big difference as shown above.
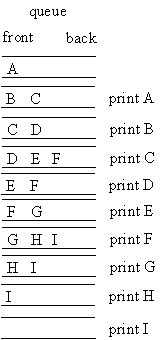
level-order traversal:
Unlike the other three traversals which are easiest to see as a recursive algorithm, level-order traversal uses a queue (recall recursion implicitly uses a stack). In this traversal, you visit all nodes with the same level (same depth) where you do the normal convention of visiting the left child first. For our example from the other 3 you would get for output: A B C D E F G H I
If you replace the key with a number representing the order in which the nodes are visited in a level-order traversal you get:
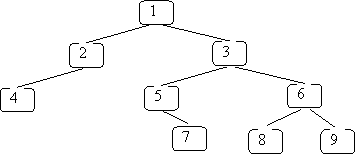The pseudo-code is:
enqueue root
while (queue not empty) {
x = dequeue
print data at x
if (there is a left child of x) {
enqueue left child of x
}
if (there is a right child of x) {
enqueue right child of x
}
}
For our standard example this gives:
The book talks about iterators on trees. They are the same idea as a linked list but the mechanics are different. How you advance depends on the ordering.
A good exercise is to calculate the height of a tree recursively. It is shown in section 17.3.