CS/ECE 252 Introduction to Computer Engineering

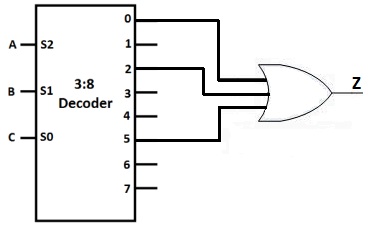
Implement the following truth table, in which A, B and C are in the inputs and Z is the output, using a 3:8 decoder and a 3-input OR gate. Use Figure 1 to represent the 3:8 decoder.

Problem 2 (2 points)

Suppose the number of address bits in memory is decreased by 8 bits and the addressability is doubled. By what factor has the size of memory changed relative to the original one?

2^-7

Problem 3 (4 points)

An instruction takes 7 cycles to execute in a processor with a clock frequency of 70 MHz. Find the following:

1. Clock cycle period

   1/(clock frequency) = 10^-7/ 7

2. Instructions per second

   (70 * 10⁶ cycles/second) / (7 cycles/instruction) = 10⁷ instructions/second

3. What is the execution time of a program in which 250 instructions are executed?

   (250 instructions) / (10⁷ instructions/second) = 2.5 * 10^-5 seconds

Problem 4 (6 points)

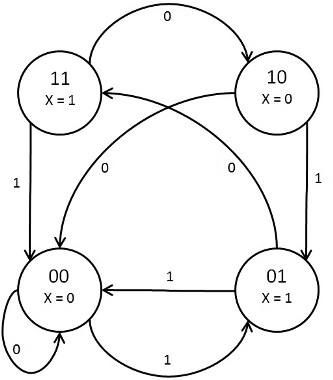
Consider the State Diagram shown below. Each state is denoted as a 2-bit value, the values on the arrows represent the input, and X in each state represents the output.

1. Fill out the Output truth table for the above state diagram.

   State	Output
   00	0
   01	1
   10	0
   11	1

2. Fill out the next state logic in a State table for the above state diagram.

   Current State	Input	Next State
   00	0	00
   00	1	01
   01	0	11
   01	1	00
   10	0	00
   10	1	01
   11	0	10
   11	1	00

3. How many storage elements (flip-flops) are needed to implement the given state machine? Explain your answer.

   Number of flops needed = Number of bits used to represent a state = 2

Problem 5 (6 points)

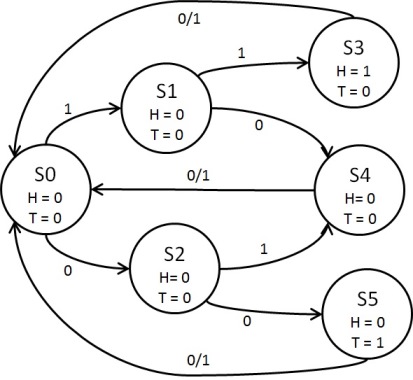
Design a Moore finite state machine (FSM) that counts the number of Heads and Tails in 2 consecutive tosses of a fair coin. The input to the FSM is a sequence of bits, where 1 represents a Head and 0 represents a Tail. After each toss, the FSM should output a 1-bit value (H) which specifies if it has seen 2 Heads and a 1-bit value (T) which specifies if it has seen 2 Tails. After every second toss, the next toss resets the system, i.e., the outputs H and T are set to 0, irrespective of whether the result of that toss is a Head or a Tail.
For example, (X shows the initial state of the system)

Input sequence  X 1 0 0 1 1 1 0 0 0 0 0 1 ...
Output H        0 0 0 0 0 1 0 0 0 0 0 0 0 ...
Output T        0 0 0 0 0 0 0 0 1 0 0 1 0 ...

S0 is the start state

Problem 6 (6 points)

Consider a machine which implements an ISA in which every instruction is 20 bits long and has the following format:

OPCODE

DR

SR1

SR2

Unused bits (if any)

Where DR = Destination register, SR1 = Source Register 1, and SR2 = Source register 2. The fields DR, SR1 and SR2 are represented using the same number of bits.

1. If the Opcode field is 5 bits wide, what is the maximum number of instructions supported by the ISA?

   2⁵ = 32

2. If the total number of bits for DR, SR1 and SR2 fields is 12, what is the total number of registers present in the machine?

   Number of bits to represent a register = 12/3 = 4
   Therefore, number of registers = 2⁴ = 16

3. What is the total number of registers if the number of unused bits is 0 and the total number of opcodes is unchanged from (a)? Show your work.

   Number of bits for DR, SR1 and SR2 = 20 - 5 = 15
   So, per register number of bits = 5
   Therefore, number of registers = 32

Problem 7 (4 points)

Consider the 6 stage Instruction Cycle as discussed in the lecture (or Section 4.3.2 or your textbook). The time taken to execute a stage of the Instruction cycle is defined as follows:

• Any stage that accesses memory (read or write) will take 10 clock cycles
• All stages that don't access memory, complete in 1 clock cycle.
• If a stage is not required in the execution an instruction, it takes 0 clock cycles to complete that stage (in other words that stage is skipped during the execution of that instruction).

1. Load a value from the memory location specified by a register R1, to a register R2.

   Fetch = 10
   Decode = 1
   Evaluate Address = 1
   Fetch Operands = 10
   Execute = 0
   Store Result = 1
   Total = 23

2. Add the values of two registers, R1 and R2, and write the result in a register R3.

   Fetch = 10
   Decode = 1
   Evaluate Address = 0
   Fetch Operands = 1
   Execute = 1
   Store Result = 1
   Total = 14

3. Store the value of a register R1 to a memory location specified by a register R2.

   Fetch = 10
   Decode = 1
   Evaluate Address = 1
   Fetch Operands = 1
   Execute = 0
   Store Result = 10
   Total = 23