CS/ECE 552-1: Introduction to Computer Architecture
Spring 2005
Problem Set #4
Problem 1 (25 points) cache mapping strategy
Problem 7.7 on page 628 of the textbook. Problem 7.20, 7.22 on page 630 of the textbook.
7.7 Here is a series of address references given as word addresses: 1, 4, 8, 5, 20, 17, 19, 56, 9, 11, 4, 43, 5, 6, 9, 17. Assuming a direct-mapped cache with 16 one-word blocks that is initially empty, label each reference in the list as a hit or a miss and show the final contents of the cache.
#of blocks = 16
|
Address reference |
Binary address |
Hit/Miss |
Assigned cache block |
|
1 |
0001 |
Miss |
0001 |
|
4 |
0100 |
Miss |
0100 |
|
8 |
1000 |
Miss |
1000 |
|
5 |
0101 |
Miss |
0101 |
|
20 |
10100 |
Miss |
0100 |
|
17 |
10001 |
Miss |
0001 |
|
19 |
10011 |
Miss |
0011 |
|
56 |
111000 |
Miss |
1000 |
|
9 |
1001 |
Miss |
1001 |
|
11 |
1011 |
Miss |
1011 |
|
4 |
0100 |
Miss |
0100 |
|
43 |
101011 |
Miss |
1011 |
|
5 |
0101 |
Hit |
0101 |
|
6 |
0110 |
Miss |
0110 |
|
9 |
1001 |
Hit |
1001 |
|
17 |
10001 |
Hit |
0001 |
Final Contents of Cache after references
|
Index |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
Contents |
|
M(17) |
|
M(19) |
M(4) |
M(5) |
M(6) |
|
|
Index |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
Contents |
M(56) |
M(9) |
|
M(43) |
|
|
|
|
7.20 Using the series of references given in Exercise 7.7, show the hits and misses and final cache contents for a two-way set-associative cache with one-word blocks and a total size of 16 words. Assume LRU replacement.
#of sets = 16 blocks /2blocks per set = 8
|
Address reference |
Binary address |
Hit/Miss |
Assigned cache set |
|
1 |
0001 |
Miss |
001 |
|
4 |
0100 |
Miss |
100 |
|
8 |
1000 |
Miss |
000 |
|
5 |
0101 |
Miss |
101 |
|
20 |
10100 |
Miss |
100 |
|
17 |
10001 |
Miss |
001 |
|
19 |
10011 |
Miss |
011 |
|
56 |
111000 |
Miss |
000 |
|
9 |
1001 |
Miss |
001 |
|
11 |
1011 |
Miss |
011 |
|
4 |
0100 |
Hit |
100 |
|
43 |
101011 |
Miss |
011 |
|
5 |
0101 |
Hit |
101 |
|
6 |
0110 |
Miss |
110 |
|
9 |
1001 |
Hit |
001 |
|
17 |
10001 |
Hit |
001 |
Final Contents of Cache after references
|
Index |
000 |
000 |
001 |
001 |
010 |
010 |
011 |
011 |
|
Contents |
M(8) |
M(56) |
M(9) |
M(17) |
|
|
M(43) |
M(11) |
|
Index |
100 |
100 |
101 |
101 |
110 |
110 |
111 |
0111 |
|
Contents |
M(4) |
M(20) |
M(5) |
|
M(6) |
|
|
|
7.22 Using the series of references given in Exercise 7.7, show the hits and misses and final cache contents for a fully associative cache with four-word blocks and a total size of 16 words. Assume LRU replacement.
# of set = 1
|
Address reference |
Binary address |
Hit/Miss |
Assigned cache block |
|
1 |
0001 |
Miss |
00 |
|
4 |
0100 |
Miss |
01 |
|
8 |
1000 |
Miss |
10 |
|
5 |
0101 |
Hit |
01 |
|
20 |
10100 |
Miss |
11 |
|
17 |
10001 |
Miss |
00 |
|
19 |
10011 |
Hit |
00 |
|
56 |
111000 |
Miss |
10 |
|
9 |
1001 |
Miss |
01 |
|
11 |
1011 |
Hit |
01 |
|
4 |
0100 |
Miss |
11 |
|
43 |
101011 |
Miss |
00 |
|
5 |
0101 |
Hit |
11 |
|
6 |
0110 |
Hit |
11 |
|
9 |
1001 |
Hit |
01 |
|
17 |
10001 |
Miss |
10 |
Final Contents of Cache after references
|
Index |
00 |
00 |
00 |
00 |
01 |
01 |
01 |
01 |
|
Contents |
M(40) |
M(41) |
M(42) |
M(43) |
M(8) |
M(9) |
M(10) |
M(11) |
|
Index |
10 |
10 |
10 |
10 |
11 |
11 |
11 |
11 |
|
Contents |
M(16) |
M(17) |
M(18) |
M(19) |
M(4) |
M(5) |
M(6) |
M(7) |
Problem 2 (10 points) cache of unusual size
Problem 7.25 on page 631 of the textbook
7.25 This exercise concerns caches of unusual sizes. Can you
make a fully associative cache containing exactly 3K words of data? How about a
set-associative cache containing exactly 3K words of data? How about a
set-associative cache or a direct-mapped cache containing exactly 3K words of
data? For each of these, describe how or why not. Remember that 1K=210
The important key to this problem is to note that anything addressed by the address must be a power of two: the number of sets, the number of words per block, the number of bytes per word, etc.
A fully associative cache containing 3K words of data is possible. There is only one set, and all words/blocks in the set have their tags checked in parallel, so there can be an odd number of words.
As for a set-associative cache, again, there only must be a power of 2 number of sets. We can make a 3-way set-associative set, with each set containing 1K words. The address looks at a set number, and the 3 blocks in that set have their tags checked in parallel.
A direct-mapped cache is not possible without extra cumbersome lookup logic (negating the access time advantage of DM caches). With a single way, all 3K blocks would have to be in that way, so 1/4 of the address space cannot be cached.
Problem 3 (15 points) Associativity & replacement policy vs. performance
Problem 7.23 on page 630 of the textbook. Please add an explanation as to why your answer is correct. An answer without explanation will NOT receive any credit.
7.23 Associativity usually improves the miss ratio, but not always. Give a short series of address references for which a two-way set-associative cache with LRU replacement would experience more misses than a direct-mapped cache of the same size.
The key to this problem is to note that two addresses that map to the same set in a set-associative cache may map to a different block in a direct-mapped cache. A simple example is with a four-word cache and 1 word blocks. The example sequence is addresses 0, 2, 4, 0, 2. In the direct-mapped cache, 0 and 4 map to block 0, while 2 maps to block 2. Accesses to 0 and 4 miss because they conflict in block 0, but the second access to 2 hits. The hit rate is 1/5
With a 2-way set-associative cache, all three address map to the first set. Thus after the first two misses, 4 kicks out 0, 0 kicks out 2, and 2 kicks out 4. The hit rate is 0/5.
Problem 4 (20 points) cache performance analysis
Exercise 7.27 on page 631 of the textbook.
7.27 Consider three machines with different cache configurations:
- Cache 1: Direct-mapped with one-word blocks
- Cache 2: Direct-mapped with four-word blocks
- Cache 3: Two-way set associative with four-word blocks
The following miss rate measurements have been made:
- Cache 1: Instruction miss rate is 4%; data miss rate is 8%.
- Cache 2: Instruction miss rate is 2%; data miss rate is 5%.
- Cache 3: Instruction miss rate is 2%; data miss rate is 4%.
For these machines, one-half of the instructions contain a data reference. Assume that the cache miss penalty is 6 + Block size in words. The CPI for this workload was measured on a machine with cache 1 and was found to be 2.0. Determine which machine spends the most cycles on cache misses.
Memory-stall clock cycles = Instructions/ Program * Misses/Instruction * Miss penalty
Misses/Instruction = Instruction miss rate + (Data miss rate* Data references/Instruction)
Miss penalty = 6 + Block size in words
Data references/Instruction = 50%
Cache 1: Block size = 1 word
Miss penalty = 6+1 =7 cycles
Instruction miss rate = 4%
Data miss rate = 8%
CPIstall
= (Instruction miss rate + (Data miss rate* Data references/Instruction) * Miss penalty
= (4% + (8%*50%)) * 7 = 0.56
CPI = CPIstall + CPIperfect = 2.0
CPIperfect = 2.0 ? 0.56 = 1.44
Cache 2:
Block size = 4 words
Miss penalty = 6+4 = 10 cycles
Instruction miss rate = 2%
Data miss rate = 5%
CPIstall
= (Instruction miss rate + (Data miss rate* Data references/Instruction) * Miss penalty
= (2% + (5%*50%)) * 10 = 0.45
Cache 3:
Block size = 4 words
Miss penalty = 6+4 = 10 cycles
Instruction miss rate = 2%
Data miss rate = 4%
CPIstall
= (Instruction miss rate + (Data miss rate* Data references/Instruction) * Miss penalty
= (2% + (4%*50%)) * 10 = 0.4
So cache 1 spends the most cycles on cache misses.
Problem 5 (15 points) virtual memory page tables
Exercise 7.32 on page 632 of the textbook.
Consider a virtual memory memory system with the following properties: 40-bit virtual byte address, 16 KB pages, 36-bit physical byte address. What is the total size of the page table with valid, protection, dirty, and use bits per entry?
With 16 KB pages, the lower 14 bits of the virtual and physical address is the page offset. 26 bits are left over in the virtual address, so the number of page table entries = 2^26. The page offset is not stored in the page table (since it is the same in the physical and virtual address), so 36 - 14 + 4 = 26 bits is stored in each entry. The total size = 2^26 * 26 bits = 208 MB. Alternatively, since 26 bits is close to 32 bits, each entry can be padded up to 4 bytes, making the total size 256 MB.
Problem 6 (15 points)
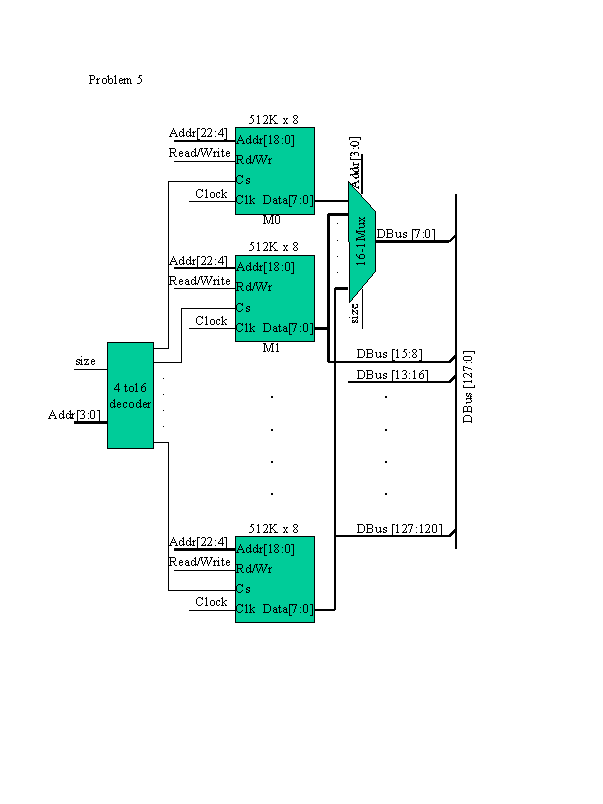
Design an 8MB memory that is 128b wide, using 512K x 8b static RAMs. Please make your figure neat and legible. Otherwise, you may lose points even if your design happens to be correct.
Note: A generally accepted notation is B for byte, b for bit, MB for megabyte, and Mb for megabit.
- Give a block diagram of the design. Describe the external interface of the 512K x 8b chip that you are using.
- Suppose the memory must be both byte and word addressable, with the mode of access specified by an extra control line called size. You will need four more address bits to specify a byte address. Modify your design to include byte addressability.
8MB memory will use
8M*8 / (512K *8) = 16 chips
128 b width will need
128/8 = 16 chips in a row
8MB memory has
8M*8 / 128 = 512K words
The 8MB memory need 19 bits as address for word access, the lower 4 bits can be used for byte access, select 1 byte from 16 bytes in a word.
When size=0, word access, the Cs outputs are all ?1?s
When size=1, byte access, the Cs outputs will be one-hot, 1 chip will be selected, Data from other chips will be ?Don?t care? in this case.