We presented processes from the “user's” point of view bottom-up: starting with the process concept, then introducing semaphores as a way of synchronizing processes, and finally adding a higher-level synchronization facility in the form of monitors. We will now explain how to implement these things in the opposite order, starting with monitors, and finishing with the mechanism for making processes run.
Some text books make a big deal out of showing that various synchronization primitives are equivalent to each other. While this is true, it kind of misses the point. It is easy to implement semaphores with monitors,
class Semaphore {
private int value;
public Semaphore(int initialValue) { value = initialValue; }
public synchronized void up() { value++; notify(); }
public synchronized void down() {
while (value == 0) wait();
value--;
}
}
but that's not the
way it usually works. Normally, semaphores (or something very like
them) are implemented using lower level facilities, and then they
are used to implement monitors.
Since monitors are a language feature, they are implemented with the help of a compiler. In response to the keywords monitor, condition, signal, wait, and notify, the compiler inserts little bits of code here and there in the program. We will not worry about how the compiler manages to do that, but only concern ourselves with what the code is and how it works.
The monitor keyword in “standard” monitors says that there should be mutual exclusion between the methods of the monitor class (the effect is similar to making every method a synchronized method in Java). Thus the compiler creates a semaphore mutex initialized to 1 and adds
muxtex.down();
to the head of each method. It also adds a chunk of code that we
call exit (described below) to each place where a method may return--at
the end of the procedure, at each return statement, at each point where
an exception may be thrown, at each place where a goto might leave the
procedure (if the language has gotos), etc. Finding all these return
points can be tricky in complicated procedures, which is why we want the
compiler to help us out.
When a process signals or notifies a condition variable on which some other process is waiting, we have a problem: We can't let both of the processes continue immediately, since that would violate the cardinal rule that there may never be more than one process active in methods of the same monitor object at the same time. Thus we must block one of the processes: the signaller in the case of signal and the waiter in the case of notify We will first show how signal-style monitors are implemented, and later show the (simpler) solution for notify-style monitors.
When a process calls signal, it blocks itself on a semaphore we will call highPriority since processes blocked on it are given preference over processes blocked on mutex trying to get in “from the outside.” We will also need to know whether any process is waiting for this semaphore. Since semaphores have no method for asking whether anybody is waiting, we will use an ordinary integer variable highCount to keep track of the number of processes waiting for highPriority. Both highPriority and highCount are initialized to zero.
Each condition variable c is replaced by a semaphore cSem, initialized to zero, and an integer variable cCount, also initialized to zero. Each call c.wait() becomes
cCount++;
if (highCount > 0)
highPriority.up();
else
mutex.up();
cSem.down();
cCount--;
Before a process blocks on a condition variable, it lets some other
process go ahead, preferably one waiting on the highPriority
semaphore.
The operation c.signal() becomes
if (cCount > 0) {
highCount++;
cSem.up();
highPriority.down();
highCount--;
}
Notice that a signal of a condition that is not awaited has
no effect, and that a signal of a condition that is awaited
immediately blocks the signaller.
Finally, the code for exit which is placed at every return point, is
if (highCount > 0)
highPriority.up();
else
mutex.up();
Note that this is the code for c.wait() with the code manipulating
cCount and cSem deleted.
If a signal call is the very last thing before a return the operations on highPriority and highCount may be deleted. If all calls of signal are at return points (not an unusual situation), highPriority and highCount can be deleted altogether, along with all code that mentions them.
The variables highCount and cCount are ordinary integer variables, so there can be problems if two or more processes try to access them at the same time. The code here is carefully written so that a process only inspects or changes one of these variables before calling up() on any semaphore that would allow another process to become active inside the monitor.
In systems that use notify (such as Java), c.notify() is replaced by
if (cCount > 0) {
cCount--;
cSem.up();
}
In these systems, the code for c.wait() also has to be modified
to delay waking up until the notifying process has blocked itself or left the
monitor.
One way to do this would be for the process to call highPriority.down
immediately after waking up from a wait. A simpler solution
(the one actually used in Java) is get rid of the highPriority
semaphore and make the waiter call mutex.down.
In summary, the code for c.wait() is
cCount++;
mutex.up();
cSem.down();
mutex.down();
and the code for exit is
mutex.up();
Note that when a language has notify instead of signal
it has to implement wait and exit differently.
No system offers both signal and notify.
In summary,
| source code | signal implementation | notify implementation |
|---|---|---|
| method start | mutex.down() | mutex.down() |
| c.wait() | cCount++; if (highCount > 0) highPriority.up(); else mutex.up(); cSem.down(); cCount--; | cCount++; mutex.up(); cSem.down(); mutex.down(); |
| c.signal() | if (cCount > 0) { highCount++; cSem.up(); highPriority.down(); highCount--; } | |
| c.notify() | if (cCount > 0) { cCount--; cSem.up(); } | |
| c.notifyAll() | while (cCount > 0) { cCount--; cSem.up(); } | |
| method exit | if (highCount > 0) highPriority.up(); else mutex.up(); mutex.up();
| |
Finally, note that we do not use the full generality of semaphores in
this implementation of monitors.
The semaphore mutex only takes on the values 0 and 1 (it is a
so-called binary semaphore) and the other semaphores never
have any value other than zero.
Implementing Semaphores
A simple-minded attempt to implement semaphores might look like this:
class Semaphore {
private int value;
Semaphore(int v) { value = v; }
public void down() {
while (value == 0) {}
value--;
}
public void up() {
value++;
}
}
There are two things wrong with this solution:
First, as we have seen before, attempts to manipulate a shared variable without
synchronization can lead to incorrect results, even
if the manipulation is as simple as value++.
If we had monitors, we could make the modifications of value atomic
by making the class into a monitor (or by making each method
synchronized), but remember that monitors are implemented with
semaphores, so we have to implement semaphores with something even more
primitive.
For now, we will assume that we have critical sections:
If we bracket a section of code with beginCS and endCS,
beginCS()
do something;
endCS()
the code will execute atomically, as if it were protected by a semaphore
mutex.down();
do something;
mutex.up();
where mutex is a semaphore initialized to 1.
Of course, we can't actually use a semaphore to implement semaphores!
We will show how to implement beginCS and endCS in the
next section.
The other problem with our implementation of semaphores is that it includes a busy wait. While Semaphore.down() is waiting for value to become non-zero, it is looping, continuously testing the value. Even if the waiting process is running on its own CPU, this busy waiting may slow down other processes, since it is repeatedly accessing shared memory, thus interfering with accesses to that memory by other CPU's (a shared memory unit can only respond to one CPU at a time). If there is only one CPU, the problem is even worse: Because the process calling down() is running, another process that wants to call up() may not get a chance to run. What we need is some way to put a process to sleep. If we had semaphores, we could use a semaphore, but once again, we need something more primitive.
For now, let us assume that there is a data structure called a PCB (short for “Process Control Block”) that contains information about a process, and a procedure swapProcess that takes a pointer to a PCB as an argument. When swapProcess(pcb) is called, state of the currently running process (the one that called swapProcess) is saved in pcb and the CPU starts running the process whose state was previously stored in pcb instead. Given beginCS, endCS, and swapProcess, the complete implementation of semaphores is quite simple (but very subtle!).
class Semaphore {
private PCBqueue waiters; // processes waiting for this Semaphore
private int value; // if negative, number of waiters
private static PCBqueue ready; // list of all processes ready to run
Semaphore(int initialValue) { value = initialValue; }
public void down() {
beginCS()
value--;
if (value < 0) {
// The current process must wait
// Find some other process to run instead
PCB pcb = ready.removeElement();
swapProcess(pcb);
// Now pcb contains the state of the process that called
// down(), and the currently running process is some
// other process.
waiters.addElement(pcb);
}
endCS
}
public void up() {
beginCS()
value++;
if (value <= 0) {
// The value was previously negative, so there is
// some process waiting. We must wake it up.
PCB pcb = waiters.removeElement();
ready.addElement(pcb);
}
endCS
}
} // Semaphore
Although a semaphore can never have a negative value, the implementation
allows the private value field to go below zero. If s.value ==
n, where n is zero or positive, s represents a
semaphore with value n. If s.value ==
-n, where n is positive, s represents a
semaphore with value 0 and also indicates that waiters.size() ==
n (there are n processes waiting to do
down operations on it). As the comments indicate, this coding trick
prevents the implementation from calling waiters.removeElement() when
waiters is empty. But is is possible that it calls
ready.removeElement() when ready is empty?
If there is only one CPU, that situation can only arise in the case of a global
deadlock (all processes are waiting to do down on various semaphores).
However, if there are multiple CPUs, it will happen whenever the number of
ready processes is less than the number of CPUs. For a multiple-cpu system,
the code needs to be modified to add a busy wait, something like this:
while (read.empty()) { /* do nothing */ }
PCB pcb = ready.removeElement();
The implementation of swapProcess is “magic”:
/* This procedure is probably really written in assembly language,
* but we will describe it in Java. Assume the CPU's current
* stack-pointer register is accessible as "CPU.sp".
*/
void swapProcess(PCB pcb) {
int newSP = pcb.savedSP; // (s1)
pcb.savedSP = CPU.sp; // (s2)
CPU.sp = newSP; // (s3)
}
As we mentioned
earlier,
each process has its own stack with a stack frame for
each procedure that process has called but not yet completed.
Each stack frame contains, at the very least, enough information
to implement a return from the procedure:
the address of the instruction that called the procedure, and a pointer
to the caller's stack frame.
It also contains space for all variables declared inside the procedure.
Each CPU devotes one of its registers (call it SP) to point to
the current stack frame of the process it is currently running.
When the CPU encounters a return statement, it reloads its
SP and PC (program counter) registers from the stack frame.
An approximate description in pseudo-Java might be something like this.
class StackFrame {
InstructionAddress callersPC;
StackFrame callersSP;
// space for local variables
}
class CPU {
static StackFrame sp; // the current stack pointer
static InstructionAddress pc; // the program counter
// other registers, condition codes, etc.
}
// Here's the code generated by the compiler for a procedure call
StackFrame newSP = new StackFrame(); // (c1)
newSP.callersSP = CPU.sp; // (c2)
newSP.callersPC = returnAddress; // (c3)
CPU.sp = newSP; // (c4)
goto startOfProcedure; // (c5)
returnAddress:
// And here's the code generated for a return statement
register InstructionAddress rtn = CPU.sp.callersPC; // (r1)
CPU.sp = CPU.sp.callersSP; // (r2)
goto rtn; // (r3)
Of course, there isn't really a goto statement in Java, and this
would all be done in the hardware or a sequence of assembly language
statements. Notice that rtn is declared to be a register
variable (another feature not available in Java). Otherwise, the space
for rtn would be inside the procedure's stack frame.
Statement (r2) removes that stack frame, so statement (r3) would not be able
to access the variable rtn. Most modern CPU's have a single
instruction that has the effect of statements (r1) to (r3).
Suppose process P0 calls swapProcess(pcb), where
pcb.savedSP points to a stack frame representing a call of
swapProcess by some other process P1.
Statements (c1)-(c4) in the call to swapProcess create a frame on
P0's stack and makes CPU.sp point to it.
Statement (s2) in swapProcess saves a pointer to that stack
frame in pcb.
Statement (s3) then loads SP with a pointer to P1's
stack frame for swapProcess.
Now, when the procedure returns, statement (r1) will cause rtn to point
to whatever procedure called swapProcess in process P1,
statement (r2) will make the CPU point to P1's stack, and (r3) will cause
P1 to resume execution just after its call to swapProcess.
Implementing Critical Sections
[Silb., 6th ed, Section 7.2]
The final piece in the puzzle is to implement beginCS and endCS. There are several ways of doing this, depending on the hardware configuration. First suppose there are multiple CPU's accessing a single shared memory unit. Generally, the memory or bus hardware serializes requests to read and write memory words. For example, if two CPU's try to write different values to the same memory word at the same time, the net result will be one of the two values, not some combination of the values. Similarly, if one CPU tries to read a memory word at the same time another modifies it, the read will return either the old or new value--it will not see a “half-changed” memory location. Surprisingly, that is all the hardware support we need to implement critical sections.
The first solution to this problem was discovered by the Dutch mathematician T. Dekker. A simpler solution was later discovered by Gary Peterson [Silb., 6th ed, Figure 7.4, p. 195]. Peterson's solution looks deceptively simple. To see how tricky the problem is, let us look at a couple of simpler--but incorrect--solutions. For now, we will assume there are only two processes, P0 and P1. The first idea is to have the processes take turns.
shared int turn; // 0 or 1
void beginCS(int i) { // process i's version of beginCS
while (turn != i) { /* do nothing */ }
}
void endCS(int i) { // process i's version of endCS
turn = 1 - i; // give the other process a chance.
}
This solution is certainly safe, in that it never allows both
processes to be in their critical sections at the same time.
The problem with this solution is that it is not live.
If process P0 wants to enter its critical section and turn == 1,
it will have to wait until process P1 decides to enter and then
leave its critical section.
Since we will only used critical sections to protect short operations
(see the implementation of semaphores
above), it is reasonable to assume that
a process that has done beginCS will soon do endCS,
but the converse is not true: There's no reason to assume that the
other process will want to enter its critical section any time in the
near future (or even at all!).
To get around this problem, a second attempt to solve the problem uses a shared array critical to indicate which processes are in their critical sections.
shared boolean critical[] = { false, false };
void beginCS(int i) {
critical[i] = true;
while (critical[1 - i]) { /* do nothing */ }
}
void endCS(int i) {
critical[i] = false;
}
This solution is unfortunately prone to deadlock.
If both processes set their critical flags to true at
the same time, they will each loop forever, waiting for the other
process to go ahead.
If we switch the order of the statements in beginCS, the solution
becomes unsafe.
Both processes could check each other's critical states at the same
time, see that they were false, and enter their critical sections.
Finally, if we change the code to
void beginCS(int i) {
critical[i] = true;
while (critical[1 - i]) {
critical[i] = false;
/* perhaps sleep for a while */
critical[i] = true;
}
}
livelock can occur.
The processes can get into a loop in which each process sets its own
critical flag, notices that the other critical flag is
true, clears its own critical flag, and repeats.
Peterson's (correct) solution combines ideas from both of these attempts. Like the second “solution,” each process signals its desire to enter its critical section by setting a shared flag. Like the first “solution,” it uses a turn variable, but it only uses it to break ties.
shared int turn;
shared boolean critical[] = { false, false };
void beginCS(int i) {
critical[i] = true; // let other guy know I'm trying
turn = 1 - i; // be nice: let him go first
while (
critical[1-i] // the other guy is trying
&& turn != i // and he has precedence
) { /* do nothing */ }
}
void endCS(int i) {
critical[i] = false; // I'm done now
}
Peterson's solution, while correct, has some drawbacks. First, it employs a busy wait (sometimes called a spin lock) which is bad for reasons suggested above. However, if critical sections are only used to protect very short sections of code, such as the down and up operations on semaphores as above, this isn't too bad a problem. Two processes will only rarely attempt to enter their critical sections at the same time, and even then, the loser will only have to “spin” for a brief time. A more serious problem is that Peterson's solution only works for two processes. Next, we present three solutions that work for arbitrary numbers of processes.
Most computers have additional hardware features that make the critical section easier to solve. One such feature is a “test and set” instruction that sets a memory location to true and at the same time loads the previous value of that memory location into the CPU. For example, the old value might be loaded into a register, or a condition code might be set to indicate whether the old value was false. The text presents a solution using test-and-set [Silb., 6th ed, Figure 7.7, p. 198] [Tanenbaum, Figure 2-22, p 105]. Here is a version using Java-like syntax
shared boolean lock = false; // true if any process is in its CS
void beginCS() { // same for all processes
for (;;) {
register boolean key = testAndSet(lock);
if (!key)
break;
}
}
void endCS() {
lock = false;
}
Some other computers have a swap instruction that swaps the
value in a register with the contents of a shared memory word.
shared boolean lock = false; // true if any process is in its CS
register boolean key = true; // each thread has its own copy of this
void beginCS() { // same for all processes
for (;;) {
swap(key, lock)
if (!key)
return;
}
}
void endCS() {
swap(key, lock)
}
The problem with both of these solutions is that they do not necessarily prevent starvation. If several processes try to enter their critical sections at the same time, only one will succeed (safety) and the winner will be chosen in a bounded amount of time (liveness), but the winner is chosen essentially randomly, and there is nothing to prevent one process from winning all the time. The “bakery algorithm” of Leslie Lamport solves this problem [Silb., 6th ed, Figure 7.5, p. 197]. When a process wants to get service, it takes a ticket. The process with the lowest numbered ticket is served first. The process id's are used to break ties.
static final int N = ...; // number of processes
shared boolean choosing[] = { false, false, ..., false };
shared int ticket[] = { 0, 0, ..., 0 };
void beginCS(int i) {
choosing[i] = true;
ticket[i] = 1 + max(ticket[0], ..., ticket[N-1]);
choosing[i] = false;
for (int j=0; j<N; j++) {
while (choosing[j]) { /* nothing */ }
while (ticket[j] != 0
&& (
ticket[j] < ticket[i]
|| (ticket[j] == ticket[i] && j < i)
) { /* nothing */ }
}
}
void endCS(int i) {
ticket[i] = 0;
}
Finally, we note that all of these solutions to the critical-section
problem assume multiple CPU's sharing one memory.
If there is only one CPU, we cannot afford to busy-wait.
However, the good news is that we don't have to.
All we have to do is make sure that the short-term scheduler (to be
discussed in the next section) does not switch processes while
a process is in a critical section.
One way to do this is simply to block interrupts.
Most computers have a way of preventing interrupts from occurring.
It can be dangerous to block interrupts for an extended period of time,
but it's fine for very short critical sections, such as the ones used
to implement semaphores.
Note that a process that blocks on a semaphore does not need mutual exclusion
the whole time it's blocked; the critical section is only long enough to
decide whether to block.
Short-term Scheduling
Earlier, we called a process that is not blocked “runnable” and said that a runnable process is either ready or running. In general, there is a list of runnable processes called the ready list. Each CPU picks a process from the ready list and runs it until it blocks. It then chooses another process to run, and so on. The implementation of semaphores above illustrates this. This switching among runnable processes is called short-term scheduling 1 and the algorithm that decides which process to run and how long to run it is called a short-term scheduling policy or discipline. Some policies are preemptive, meaning that the CPU may switch processes even when the current process isn't blocked.
Before we look at various scheduling policies, it is worthwhile to think about what we are trying to accomplish. There is a tension between maximizing overall efficiency and giving good service to individual “customers.” From the system's point of view, two important measures are

Each “job”2 also wants good service. In general, “good service” means good response: It is starts quickly, runs quickly, and finishes quickly. There are several ways of measuring response:
Since we are concentrating on short-term (CPU) scheduling, one useful way to look at a process is as a sequence of bursts. Each burst is the computation done by a process between the time it becomes ready and the next time it blocks. To the short-term scheduler, each burst looks like a tiny “job.”
The simplest possible scheduling discipline is called First-come, first-served (FCFS). The ready list is a simple queue (first-in/first-out). The scheduler simply runs the first job on the queue until it blocks, then it runs the new first job, and so on. When a job becomes ready, it is simply added to the end of the queue.
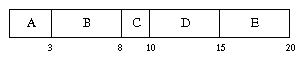
Here's an example, which we will use to illustrate all the scheduling disciplines.
| Burst | Arrival Time | Burst Length |
|---|---|---|
| A | 0 | 3 |
| B | 1 | 5 |
| C | 3 | 2 |
| D | 9 | 5 |
| E | 12 | 5 |
The main advantage of FCFS is that it is easy to write and understand, but it has some severe problems. If one process gets into an infinite loop, it will run forever and shut out all the others. Even if we assume that processes don't have infinite loops (or take special precautions to catch such processes), FCFS tends to excessively favor long bursts. Let's compute the waiting time and penalty ratios for these jobs.
| Burst | Start Time | Finish Time | Waiting Time | Penalty Ratio |
|---|---|---|---|---|
| A | 0 | 3 | 0 | 1.0 |
| B | 3 | 8 | 2 | 1.4 |
| C | 8 | 10 | 5 | 3.5 |
| D | 10 | 15 | 1 | 1.2 |
| E | 15 | 20 | 3 | 1.6 |
| Average | 2.2 | 1.74 |
Favoring long bursts means favoring CPU-bound processes (which have very long CPU bursts between I/O operations). In general, we would like to favor I/O-bound processes, since if we give the CPU to an I/O-bound process, it will quickly finish its burst, start doing some I/O, and get out of the ready list. Consider what happens if we have one CPU-bound process and several I/O-bound processes. Suppose we start out on the right foot and run the I/O-bound processes first. They will all quickly finish their bursts and go start their I/O operations, leaving us to run the CPU-bound job. After a while, they will finish their I/O and queue up behind the CPU-bound job, leaving all the I/O devices idle. When the CPU-bound job finishes its burst, it will start an I/O operation, allowing us to run the other jobs. As before, they will quickly finish their bursts and start to do I/O. Now we have the CPU sitting idle, while all the processes are doing I/O. Since the CPU hog started its I/O first, it will likely finish first, grabbing the CPU and making all the other processes wait. The system will continue this way, alternating between periods when the CPU is busy and all the I/O devices are idle with periods when the CPU is idle and all the processes are doing I/O. We have destroyed one of the main motivations for having processes in the first place: to allow overlap between computation with I/O. This phenomenon is called the convoy effect.
In summary, although FCFS is simple, it performs poorly in terms of
global performance measures, such as CPU utilization and throughput.
It also gives lousy response to interactive jobs (which tend to be
I/O bound).
The one good thing about FCFS is that there is no starvation:
Every burst does get served, if it waits long enough.
Shortest-Job-First
A much better policy is called shortest-job-first (SJF). Whenever the CPU has to choose a burst to run, it chooses the shortest one. (The algorithm really should be called “shortest burst first”, but the name SJF is traditional). This policy certainly gets around all the problems with FCFS mentioned above. In fact, we can prove the SJF is optimal with respect to average waiting time. That is, any other policy whatsoever will have worse average waiting time. By decreasing average waiting time, we also improve processor utilization and throughput.
Here's the proof that SJF is optimal. Suppose we have a set of bursts ready to run and we run them in some order other than SJF. Then there must be some burst that is run before shorter burst, say b1 is run before b2, but b1 > b2. If we reversed the order, we would increase the waiting time of b1 by b2, but decrease the waiting time of b2 by b1. Since b1 > b2, we have a net decrease in total, and hence average, waiting time. Continuing in this manner to move shorter bursts ahead of longer ones, we eventually end up with the bursts sorted in increasing order of size (think of this as a bubble sort!).
Here's our previous example with SJF scheduling
| Burst | Start Time | Finish Time | Waiting Time | Penalty Ratio |
|---|---|---|---|---|
| A | 0 | 3 | 0 | 1.0 |
| B | 5 | 10 | 4 | 1.8 |
| C | 3 | 5 | 0 | 1.0 |
| D | 10 | 15 | 1 | 1.2 |
| E | 15 | 20 | 3 | 1.6 |
| Average | 1.6 | 1.32 |

As described, SJF is a non-preemptive policy. There is also a preemptive version of the SJF, which is sometimes called shortest-remaining-time-first (SRTF). Whenever a new job enters the ready queue, the algorithm reconsiders which job to run. If the new arrival has a burst shorter than the remaining portion of the current burst, the scheduler moves the current job back to the ready queue (to the appropriate position considering the remaining time in its burst) and runs the new arrival instead.
With SJF or SRTF, starvation is possible. A very long burst may never get run, because shorter bursts keep arriving in the ready queue. We will return to this problem later.
There's only one problem with SJF (or SRTF): We don't know how long a burst is going to be until we run it! Luckily, we can make a pretty good guess. Processes tend to be creatures of habit, so if one burst of a process is long, there's a good chance the next burst will be long as well. Thus we might guess that each burst will be the same length as the previous burst of the same process. However, that strategy won't work so well if a process has an occasional oddball burst that unusually long or short burst. Not only will we get that burst wrong, we will guess wrong on the next burst, which is more typical for the process. A better idea is to make each guess the average of the length of the immediately preceding burst and the guess we used before that burst: guess = (guess + previousBurst)/2. This strategy takes into account the entire past history of a process in guessing the next burst length, but it quickly adapts to changes in the behavior of the process, since the “weight” of each burst in computing the guess drops off exponentially with the time since that burst. If we call the most recent burst length b1, the one before that b2, etc., then the next guess is b1/2 + b2/4 + b4/8 + b8/16 + ....
Another scheme for preventing long bursts from getting too much priority is a preemptive strategy called round-robin (RR). RR keeps all the bursts in a queue and runs the first one, like FCFS. But after a length of time q (called a quantum), if the current burst hasn't completed, it is moved to the tail of the queue and the next burst is started. Here are Gantt charts of our example with round-robin and quantum sizes of 4 and 1.
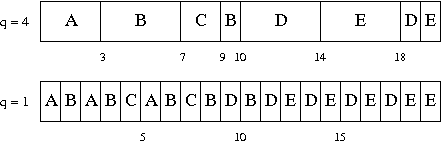
The limit, as q approaches zero, is called processor sharing (PS). PS causes the CPU to be shared equally among all the ready processes. In the steady state of PS, when no bursts enter or leave the ready list, each burst sees a penalty ratio of exactly n, the length of the ready queue. In this particular example, burst A arrives at time 0 and for one millisecond, it has the CPU to itself, so when B arrives at time 1, A has used up 1 ms of its demand and has 2 ms of CPU demand remaining. From time 1 to 3, A and B share the CPU equally. Thus each of them gets 1 ms CPU time, leaving A with 1 ms remaining and B with 4 ms remaining. After C arrives at time 3, there are three bursts sharing the CPU, so it takes 3 ms -- until time 6 -- for A to finish. Continuing in a similar manner, you will find that for this example, PS gives exactly the same results as RR with q = 1. Of course PS is only of theoretical interest. There is a substantial overhead in switching from one process to another. If the quantum is too small, the CPU will spend most its time switching between processes and practically none of it actually running them!
There are a whole family of scheduling algorithms that use priorities. The basic idea is always to run the highest priority burst. Priority algorithms can be preemptive or non-preemptive (if a burst arrives that has higher priority than the currently running burst, does do we switch to it immediately, or do we wait until the current burst finishes?). Priorities can be assigned externally to processes based on their importance. They can also be assigned (and changed) dynamically. For example, priorities can be used to prevent starvation: If we raise the priority of a burst the longer it has been in the ready queue, eventually it will have the highest priority of all ready burst and be guaranteed a chance to finish. One interesting use of priority is sometimes called multi-level feedback queues (MLFQ). We maintain a sequence of FIFO queues, numbered starting at zero. New bursts are added to the tail of queue 0. We always run the burst at the head of the lowest numbered non-empty queue. If it doesn't complete in complete within a specified time limit, it is moved to the tail of the next higher queue. Each queue has its own time limit: one unit in queue 0, two units in queue 1, four units in queue 2, eight units in queue 3, etc. This scheme combines many of the best features of the other algorithms: It favors short bursts, since they will be completed while they are still in low-numbered (high priority) queues. Long bursts, on the other hand, will be run with comparatively few expensive process switches.
This idea can be generalized. Each queue can have its own scheduling discipline, and you can use any criterion you like to move bursts from queue to queue. There's no end to the number of algorithms you can dream up.
It is possible to analyze some of these algorithms mathematically. There is a whole branch of computer science called “queuing theory” concerned with this sort of analysis. Usually, the analysis uses statistical assumptions. For example, it is common to assume that the arrival of new bursts is Poisson: The expected time to wait until the next new burst arrives is independent of how long it has been since the last burst arrived. In other words, the amount of time that has passed since the last arrival is no clue to how long it will be until the next arrival. You can show that in this case, the probability of an arrival in the next t milliseconds is
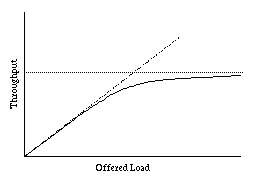
The ratio ρ = α/β is of particular interest. If ρ > 1, bursts are arriving, on the average, faster than they are finishing, so the ready queue grows without bound. (Of course, that can't happen because there is at most one burst per process, but this is theory!) If ρ = 1, arrivals and departures are perfectly balanced.
It can be shown that for FCFS, the average penalty ratio for bursts of length t is
For processor sharing, as we noticed above, all processes have a penalty ratio that is the length of the queue. It can be shown that on the average, that length is 1/(1−ρ).
1We will see medium-term and long-term scheduling later in the course.
2A job might be a batch job (such as printing a run of paychecks), an interactive login session, or a command issued by an interactive session. It might consist of a single process or a group of related processes.