Section#14: All-to-all scatter algorithms
(CS838: Topics in parallel computing, CS1221, Thu, Mar 18, 1999, 8:00-9:15 a.m.)
The contents
- Combining model with SF switching
- Hypercube
- 1-D torus
- Higher-dimensional mesh/torus
- Combining model with WH switching
- Hypercube
- Meshes/tori
- Noncombining model with SF switching
- All-port full-duplex hypercube
- Noncombining model with WH switching
- Direct exchange AAS on hypercube
- Meshes/tori
In all-to-all scatter, called also complete exchange or all-to-all personalized communication, every node holds N-1 packets of size \mu, one specific packet for every other node. The total number of packets is therefore N(N-1) and the lower bound on the number of rounds is determined by the bisection width or the overall communication throughput of the network.
A typical application which requires AAS is a transposition of a matrix AN,N, mapped row-wise to N-node distributed memory machine. Each node i owns row i of AN,N and an element ai,j of AN,N, 0<= i,j<= N-1, is stored in i's local memory location j. It is easy to see that a parallel transposition of AN,N, when elements ai,j and aj,i exchange their positions in distributed memory, corresponds exactly to an AAS. Each node i has to exchange an element with every other node k, i\not=k.
Combining model with SF switching
Hypercube
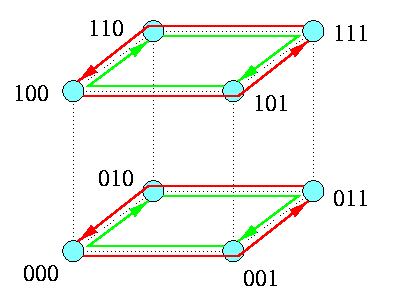
An obvious algorithm for AAS is called the standard exchange (SEX) and it is based on recursive dividing the cube into half subcubes. SEX in Qn is just a sequence of n rounds, each implementing a perfect matching: in round i, i=1,...,n, every node takes all the 2n-1=N/2 packets destined for the nodes in the opposite subcube of dimension n-i, permutes and combines them into one block, sends them to its counterpart in the matching, receives reciprocally its block, and adds the new packets to its pool of packets. The blocks of packets have the same size in all the rounds. The communication time is
tAAS(Qn,\mu)=n(ts + \mu tm2n-1).
Figure shows the first two rounds of AAS on Q3. Note that in both rounds, messages consist of 4 packets. In the first round, one node sends 4 distinct packets destined for the opposite 2-cube. In the second round, each node sends its own two packets and 2 packets from its first-round partner to the opposite 1-cube. In round 3, each node will send all 4 packets from its 2-cube destined exclusively for its partner in the last perfect matching.
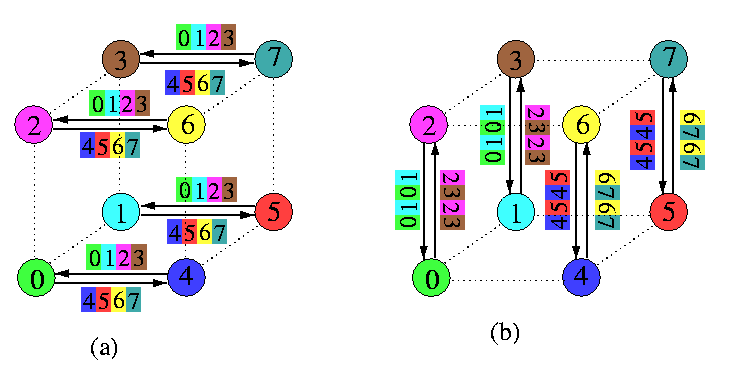
CAPTION: The first 2 rounds of a 3-round AAS in a combining 1-port hypercube Q3.
1-D torus
1-port half-duplex links
A naive trivial scheme, which is surprisingly optimal, is to pipeline cyclically all the messages. Each node forms a combined message of size (z-1)\mu and sends it to its right successor. In each round k < z, each node receives from its left neighbor a combined message of size (z-k+1)\mu, extracts from it one packet destined for himself, and forwards the remaining part of the message of size (z-k)\mu to the right. The communication time is
tAAS(T(z),\mu)=\sumi=1z-1(ts+\mu tm(z-i))=(ts + \mu tmz/2)(z-1).
It can be shown that this is optimal with respect to communication bandwidth of T(z). The number of rounds equals to the diameter of oriented T(z). The total communication work is z times the work of one OAS, which is \mu tm(\sumi=1z-1i)=z(z-1)\mu tm/2 and this work must be carried by z edges. That is why wormhole routing requires the same number of rounds and cannot improve anything.
CAPTION: AAS on a 1-port half-duplex combining SF cycle T(8)
All-port full-duplex links
All-port assumption allows to reduce the number of rounds and the total communication latency to at least one half, messages will be pipelined in both directions and will be smaller. For example, for z odd,
tAAS(T(z),\mu)=\sumi=1(z-1)/2(ts+\mu tm((z+1)/2-i))=ts(z-1)/2 + \mu tmz2/8.
Higher-dimensional mesh/torus
Lower bound on the communication latency
The lower bound for higher dimensional meshes can be derived similarly.
Lemma
Consider n-dimensional T(z1,...,zn) such that for all i, zi>= zi+1. The lower bound on the communication latency of AAS is
1/2[z1/2] [z1/2] \Pii=2n zi.
Proof
Cut T(z1,...,zn into T1=T([ z1/2],...,zn) and T2=T([ z1/2],...,zn). The number of full-duplex channels joining T1 with T2 is 2\Pii=2n zi. The amount of data that must be exchanged between T1 and T2 is |V(T1)|.|V(T2)|=[ z1/2][ z1/2]\Pii=2n zi2.
A usual approach is to apply cartesian product decomposition. Perform AAS in one dimension in all corresponding submeshes/subtori in parallel, then in second dimension, and so forth. For simplicity, consider only T(z,z). Each node must send z2-1 packets in total. First, nodes form z-1 messages for one column each, and combine them together into messages of size z(z-1)\mu, and pipeline them within all rows in parallel. Each receiver extracts z packets destined for its column, stores them, and forwards the rest. After the row AAS is finished, each node has packets from all z-1 colleagues within its row plus its own packets destined for its column. So the column AAS has exactly the same complexity and communication pattern as the row ASS.
tAAS(T(z,z))=2\sumi=1z-1(ts+\mu tmz(z-i))=(2ts+\mu tmz2)(z-1).
Analogous algorithm for 2-D mesh is similar.
Combining model with WH switching
Hypercube
Even with WH switching, we can apply the SF scheme from Subsection . Whether it will provide an optimal performance or not, depends on the ratio between ts and \mu tm. If ts\approx \mu tm, then SF algorithm will be optimal. Otherwise, distance insensitive routing can reduce the communication latency. Let us prove that SF is not optimal under these conditions.
In SF hypercube Qn, 2n(2n-1) packets of size \mu must be transmitted over distances from 1 to n and the average distance is n/2. Hence the total communication work is \mu tm2n(2n-1)n/2. The total number of arcs of Qn is n2n, and therefore the lower bound on the communication latency is
(\mu tm2n(2n-1)n/2)/(n2n)=\mu tm(2n-1)/2,
which is n times less than the latency provided by SF perfect-matching algorithm in Subsection . There really exists an optimal AAS algorithm for WH hypercubes, but surprisingly, it does not use the packet combining! We will introduce it in Subsection .
Meshes/tori
Similarly to one-to-all communication, a simple approach in low-dimensional WH meshes is to simulate AAS on SF hypercubes. Of course, it works best on meshes with side lengths equal to powers of two.
Binary exchange AAS (BEX)
The idea of the first solution for 2-D mesh, called binary exchange (BEX), is depicted on Figure . Mesh \mu(2k,2l) is recursively halved, alternately in the X and Y dimensions. If k=l, then X and Y dimensions are alternated till the end and the number of phases is k+l=log N. One phase requires more rounds, due to WH channel contention. In each round, a block of N/2 packets is exchanged between partners and packets must be then reorganized into new blocks exactly as in the hypercube SEX algorithm.
CAPTION: Binary exchange AAS on \mu(8,8).
If N=4k is the size of \mu(2k,2k), then the communication latency is roughly
tAAS(M(\sqrt{N},\sqrt{N}),\mu)= \sqrt{N}ts+2Ntd/3+N\sqrt{N}\mu tm.
Quadrant exchange AAS (QEX)
Another algorithm was designed specifically for WH meshes.
- Mesh M(2k,2k) is recursively split into quarters, one splitting corresponds to one phase.
- A phase corresponding to quarters of size 2l× 2l consists of 2l steps.
- In step i, 1<= i<= 2l, all elements on i-th diagonal of all four quarters perform a micro-AAS, represented by a rectangular in Figure (b,c).
- One micro-AAS consists in exchanging information among 4 corners of a rectangular, which takes 3 rounds, as follows form Figure (a).
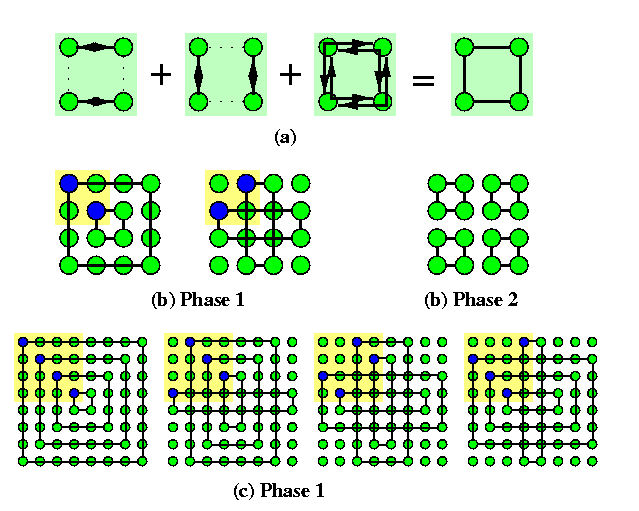
CAPTION: The idea of the quadrant-exchange AAS on WH mesh M(2k,2k). (a) The 3-round micro-AAS step between four corners of a rectangular. (b) 2 phases (2-round and 1-round ones) of AAS on M(4,4). (c) Phase 1 of QEX AAS consisting of 4 micro-AASs on M(8,8)
Noncombining model with SF switching
All-port full-duplex hypercube
In the following we will describe an both time- and transmission-optimal algorithm for AAS. The lower bound on the number of rounds is 2n-1 (see the table in Section #11.3). This optimality can be achieved only if all n2n hypercube arcs will be used at each of 2n-1 rounds and if the data are routed always along the shortest paths. For simplicity assume that it is the matrix-transposition AAS. Hence, consider a matrix AN,N, where N=2n, stored row-wise in Qn so that each node Pi owns row i of AN,N and an element ai,j of AN,N, 0<= i,j<= N-1, is stored in its local memory location j. Each node Pi, 0<= i<= N-1, has to exchange an element with every other node Pk, i\not=k.
Let \hmdn(i,j) denote the Hamming distance of vertices i,jin V(Qn). Let (i,j) denote the distributed-memory address of ai,j. Binary string i\XOR j will be referred to as the relative address of ai,j. During the matrix transposition, an element ai,j in Pi has to cross, in some, not yet known, order, \hmdn(i,j) hypercube arcs to get to its destination memory location i in Pj. All the neighbor-to-neighbor exchanges of data across all communication links simultaneously represent one global communication round.
Since the destination and source locations have the same relative address, the basic idea of the AAS algorithm is
to preserve the relative addresses of packets in each intermediate round.
For example, if n=5, i=5, and j=22, then three communication rounds are needed to exchange ai,j and aj,i, since \hmd5(5,22)=3. One possible relative-address-preserving path is (5,22)->(7,20)->(6,21)->(22,5).
In general, we need a scheduling table saying for every global communication round k in {1,..,2n-1} which relative addresses rk,0,...,rk,n-1 are assigned to dimensions 0,...,n-1, respectively.
In other words, in round k, all 2n elements with the same relative address rk,i, i in {0,..,n-1}, will be exchanged simultaneously along all the 2n-1 full-duplex links of direction i. Due to the all-port assumption, we can do it for all n directions simultaneously. The schedule table has 2n-1 rows (one row per one round) and n columns (one column per one direction). The elements ri,j, 1<= i<= 2n-1, 0<= j<= n-1, of the schedule table, are n-bit binary nonzero strings. Let ri,j[k], 0<= k<= n-1, denote the k-th bit of ri,j. The schedule table must fulfill the following constraints:
- (a)
- for all i (ri,j[j]=1). The j-th bit of all relative addresses in column j is 1 (since column j contains relative addresses of matrix elements that must cross arcs of direction j).
- (b)
- for all i; for all j1\not=j2 (ri,j1\not=ri,j2). Any relative address can appear at most once in each row (since data corresponding to one relative address can be sent in at most one direction in one communication round).
- (c)
- Every relative address r, r in {1,...,2n-1}, must appear exactly once in all the columns j, 0<= j<= n-1, such that r[j]=1 (since an element must cross exactly once all hypercube arcs corresponding to unity bits in its relative address).
The design of an optimal AAS algorithm in this communication model is therefore reduced to the problem of constructing the schedule table fulfilling the conditions (a)--(c). The table can be constructed for example in the following way.
Algorithm for constructing the schedule table:
Let mi=2i+1, i=0,..,2n-1-1, represented as an n-bit string. Elements ri,j, 0<= j<= n-1, are constructed from mi as follows:
- (i)
- ri,j=\nonj+1(mi) for 0<= j<= n-2 and ri,n-1=mi;
- (ii)
- swap bits 0 and j in ri,j.
Lemma
The schedule table constructed by this algorithm fulfills conditions (a)--(c).
Proof
(a) Since 2i+1 is odd and in any round (i) we never invert bit 0, swapping bits 0 and j results in ri,j[j]=1. (b) Any two numbers ri,j1 and ri,j2 differ in at least one bit due to inverting different bits in different columns in round (i). To prove that the condition (c) holds, it is sufficient to prove that ri1,j\not=ri2,j for all i1\not=i2. But this follows immediately from the fact that all mi=2i+1, i=0,..,2n-1-1, are distinct, and this property is preserved by inverting one bit and swapping two bits.
Table shows a schedule table for n=4.
| Round | j=0 | j=1 | j=2 | j=3
| |
1 | 0011 | 0110 | 1100 | 1000
| |
2 | 0001 | 0111 | 1110 | 1010
| |
3 | 0111 | 0010 | 1101 | 1100
| |
4 | 0101 | 0011 | 1111 | 1110
| |
5 | 1011 | 1110 | 0100 | 1001
| |
6 | 1001 | 1111 | 0110 | 1011
| |
7 | 1111 | 1010 | 0101 | 1101
| |
8 | 1101 | 1011 | 0111 | 1111
| |
|
CAPTION: Optimal scheduling table for AAS in all-port full-duplex SF Q4.
We assume that the schedule table is precomputed and stored in local memories of all nodes. The AAS will consist of successive communication rounds i, 1<= i<= 2n-1. In every round i, each node Pk sends the number from its memory location ri,j\XOR k along the communication link j, 0<= j<= n-1, (hence to node Pl where l=\nonj(k)) and subsequently stores the number received from link j in the opposite direction into the same memory location ri,j\XOR x.
Noncombining model with WH switching
Direct exchange AAS on hypercube
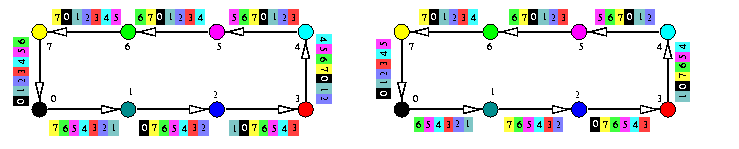
As mentioned in Subsection , if ts<< \mu tm, the standard exchange on Qn with combining packets is not optimal and there exists asymptotically optimal algorithm on WH hypercube. It is called the direct exchange (DEX) algorithm: every pair of nodes exchanges directly its two packets. The algorithm is based on a fact that e-cube routed hypercube can perform any permutation \pij: x-> x\XOR j, where j is an n-bit string, contention-free in one round (we have proved this fact in Section #10). So that DEX consists of 2n-1 permutations \pij, j=1,...,2n-1. Each node executes the following algorithm in lock-step way.
|
for i=1,...,2n-1 do
|
begin
|
mate \leftarrow {my\id()} \XOR i;
|
exchange packets with mate using e-cube routing;
|
|
]
where my\id() is a function which returns the address of the local hypercube node.
CAPTION: AAS on a noncombining WH hypercube
The communication latency of this solution is simply
tAAS(Qn,\mu)=(2n-1)(ts+ntd/2+\mu tm)
which is only twice as large as the lower bound derived in Equation in Subsection .
Meshes/tori
Hypercube DEX algorithm can be of course simulated on meshes, especially if their sizes are powers of two. If we assign binary addresses to the mesh nodes, the algorithm uses the same permutations as in the hypercube, only instead of e-cube we have XY routing. The only difference is that XY routing will produce link congestions for some permutations due to sparsity of mesh links. The maximum congestion in M(z1,z2) in any step is max(z1,z2)/2. Figure shows 6 from 7 possible permutations on M(2,4). In three of them, middle horizontal arcs suffer from link congestion 2. The exact formula for the communication latency depends on the way how the communication system handles link congestion.
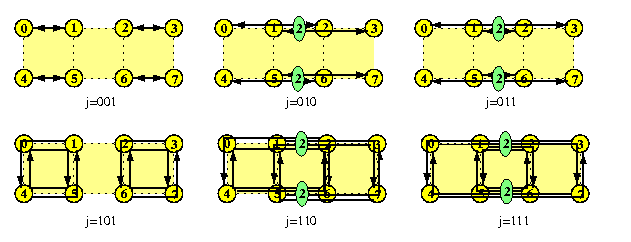
CAPTION: Direct exchange AAS on M(2,4).
Another algorithm is a little bit more involved. It also uses dimension-order routing and it achieves asymptotically optimal number of rounds even though it needs only 1-port capability! It is based on a similar idea as the quadrant-exchange algorithm, however, it works optimally for a larger family of meshes and it is not combining.
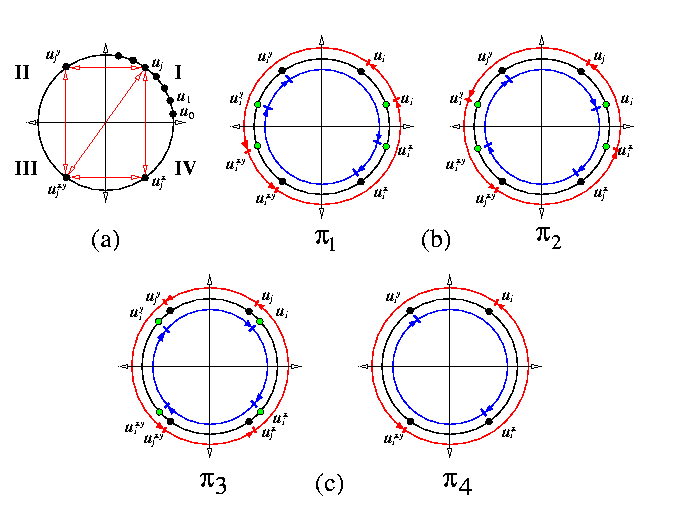
CAPTION: Direct exchange AAS on a cycle.
First, we will explain the idea of the algorithm on 1-D torus. For simplicity, assume T(z) with z=4t.
- arrange T(z) in an xy-plane as in Figure (a). The X+Y+ quadrant is called quadrant I and the other three are denoted II, III, and IV anticlockwise.
- denote nodes in quadrant I by u1,...,ut.
- denote by uix, uiy, and uixy the nodes symmetric to ui with respect to axis x, y, and origin, respectively (see Figure (a)).
- for each of t(t-1) possible pairs of distinct nodes ui and uj in quadrant I,
|
perform the following two contention-free micro-permutations (see Figure (b)).
- \pi1(ui,uj): {ui->uj,uj->uixy,uixy->ujxy,ujxy->ui;
uix->ujx,ujx->uiy,uiy->ujy,ujy->uix}
- \pi2(ui,uj): {ui->ujx,ujx->uixy,uixy->ujy,ujy->ui;
uj->uiy,uiy->ujxy,ujxy->uix uix->uj}
It follows that any possible pair of nodes on the cycle has exchanged directly packets except for quadruples ui,uix,uiy,uixy. This is performed now.
for each of possible t nodes ui in quadrant I, define uj=ui+1 \mod t and
perform the following two contention-free micro-permutations (see Figure (c)).
- \pi3(ui): {ui->uix,uix->uixy,uixy->uiy,uiy->ui;
uj->ujy,ujy->ujxy,ujxy->ujx,ujx->uj}
- \pi4(ui): {ui->uixy,uixy->ui,uix->uiy,uiy->uix}
Lemma
In T(z), this AAS takes 2[ z/2]2 rounds.
In higher-dimensional meshes, this can be generalized using the cartesian product property.
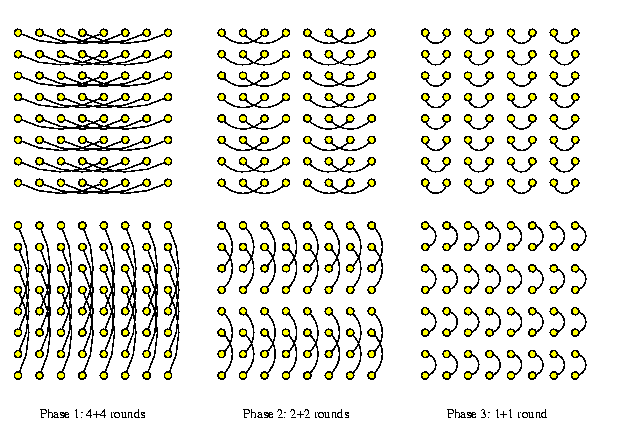
A naive solution is to apply one horizontal and one vertical micro-permutation in one round, but this decreases the efficiency. It follows that for M(z,z), where z=4t, up to t horizontal and vertical disjoint micro-permutations can be interleaved simultaneously, so that all mesh links are used in each round, as is illustrated by Figure .
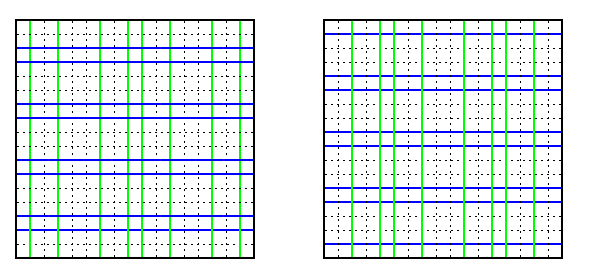
CAPTION: Interleaving of horizontal and vertical disjoint micro-permutations in M(8,8)
|








