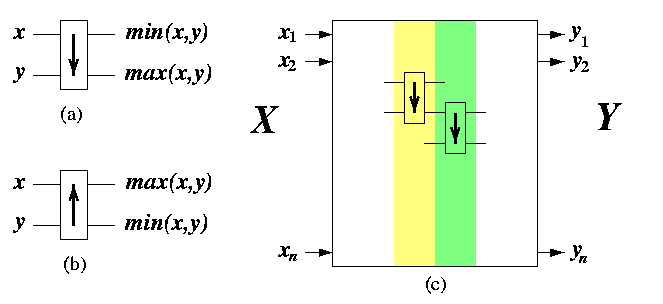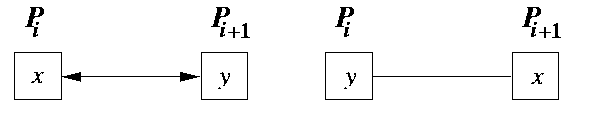Section#15: Introduction to parallel sorting on mesh-based topologies
(CS838: Topics in parallel computing, CS1221, Tue, Mar 23, 1999, 8:00-9:15 a.m.)

1. Introduction to comparison-based sorting
   1. Sorting networks
   2. Direct sorting
   3. Oblivious sorting and 0-1 lemma
2. Mesh-based oblivious sorting
   1. Even-odd transposition sorting on 1-D meshes
   2. ShearSort on 2-D meshes
   3. Lower bound on 2-D mesh snakelike sorting
   4. Lexicographic sorting on 3-D meshes

Back to the beginning of the page	Back to the CS838 class schedule

Introduction to comparison-based sorting

A vast number of parallel sorting algorithms have been described in the literature and the state-of-the-art is briefly the following:

• there exist time- and cost-optimal PRAM parallel sorting algorithms. The most fundamental is called Cole's Merge sort. It sorts N numbers in EREW PRAM memory using N processors in time O(log N). This will be covered in Section 18.
• There exist asymptotically optimal mesh-sorting algorithms. For example, N=n² numbers can be sorted on N-node 2-D mesh M(n,n) in time kn, where k is a constant between 2 and 3. This is optimal up to a multiplicative constant, since the number of sorting steps is bounded by the diameter of M(n,n), which is 2n-2. One such algorithm will be described in Section 16.
• The most important and useful parallel sorting algorithm for sorting N numbers on N-node hypercubic networks is Batcher's Merge Sort which needs O(log²N) steps. This will be covered in Section 17.
• There exist deterministic parallel algorithms for sorting N numbers on N-node hypercubic networks in O(log N(loglog N)) CE steps, but the hidden constant is very large.
• The only asymptotically cost-optimal parallel sorting algorithm is based on so called expander graphs, but these algorithms are very complicated and the hidden constants are too large so that for practical applications, the asymptotically non-optimal algorithms perform better. These two last groups of algorithms will not be covered in this course.

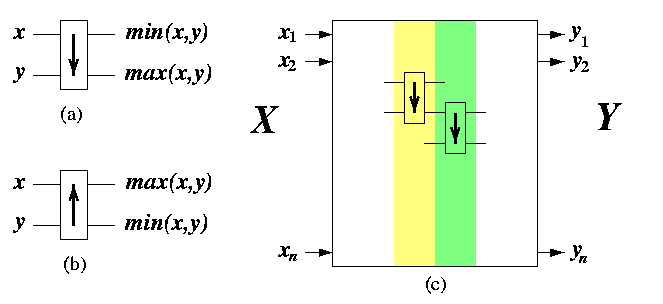
CAPTION: Architecture of comparison-exchange sorting networks. (a) The default type of comparator (b) The second type of comparator. (c) Sorting network composed from columns of basic comparators.

Sorting networks consist of comparators, which are in fact hardware implementations of the CE operation. A comparator has two inputs and two outputs. Depending on the sense of ordering, comparators can be of two kinds, see Figure (a),(b). By default, we will assume case (a). A sorting network is an end-to-end network composed of columns of comparators (see Figure (c)). It is similar to a multistage interconnection network, except that the building block is a comparator rather than a 2× 2 switch. Unsorted input sequence X=x₁,...,x_N placed on input wires of the leftmost column of comparators passes through the network so that it becomes sorted output sequence (ascending, descending, bitonic) Y=y₁,...,y_N on output wires on the rightmost column.

The way how columns of comparators are interconnected determines the sorting algorithm. We will assume static networks with fixed interconnection of comparators. Then, each sorting network is a HW implementation of a sorting algorithm whose behavior is data-insensitive: the order in which the CE operations are applied to pairs of input elements does not depend on their input values. The sorting algorithm induced by the sorting network is called oblivious. Hence, an oblivious sorting algorithm performs the same steps for randomly generated input data as for completely sorted data. Terms ``oblivious sorting algorithm'' and ``sorting network'' can be considered synonymous.

The number of parallel CE steps of an oblivious sorting algorithm is given by the depth of its sorting network. Input wires of a network have depth 0. If a comparator in the network has input wires of depth d₁ and d₂, then its output wires have depth max(d₁,d₂)+1. The depth of a sorting network is the maximum over the depths of output wires.

If N is greater than the number K of input wires of the sorting network, then we assume that the input data set is split into N/K subsequences, which are then sorted. Comparators are equipped with buffers for N/K numbers and instead of CE operation, perform Compare-and-Split (CS) operation: two input sequences are merged and split again to lower and upper half. This takes O(N/K) steps.

Direct sorting

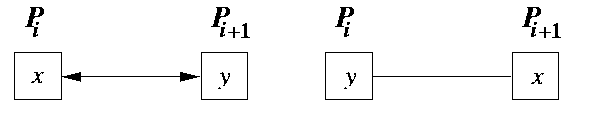
CAPTION: The effect of a compare-and-exchange operation in direct networks, if x > y.

While designing a direct sorting algorithm, we must address the following 3 issues:

• A suitable linear node indexing P₁,...,P_N. A network topology always allows various nodes indexing schemes, but those preserving adjacency are usually preferable. It is trivial if the graph has a hamiltonian path. If it is not, we know from Section #6 that there is always an indexing such that the distance between logical neighbors is at most 3. The choice of indexing scheme has impact on the complexity of sorting for given topology. Figure shows several indexing schemes suitable for meshes. The last one, denoted by zyx, applies to 3-D meshes and is called lexicographic. A 3-D point (x₁,y₁,z₁) precedes point (x₂,y₂,z₂) if z₁y₁x₁ < z₂y₂x₂, where z_iy_ix_i is viewed as a 3-digit number. Lexicographic indexing can be defined for any dimensionality.
  

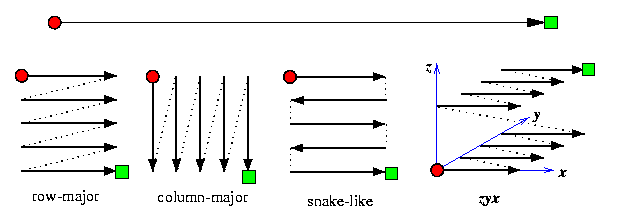
  CAPTION: Various schemes for linear indexing of mesh nodes.

• Having a node indexing, we must find perfect node matchings compliant with the indexing. Or more specifically, perfect matchings which will provide the final ordering compliant with the node indexing. One perfect matching consists of [ p/2] disjoint pairs. We will again consider only oblivious direct sorting algorithms, i.e., matchings are given irrespectively to input data values.
• scalability: If p < N, then again one node owns N/p numbers and instead of CE operations, the neighbors perform CS operations. More specifically, an oblivious sorting algorithm then consists of two parts:
  • each node sorts its N/p numbers in O((N/p)log(N/p)) steps,
  • all nodes perform the direct sorting algorithm using CS operations instead of CE.
  The CS operation between 2 nodes, say P_i and P_j, i < j, can be implemented in 2 ways.
  • (1) P_i and P_j exchange their sorted subsequences, (2) then each of them merges its subsequence with the one received from its partner into a sorted sequence of double length. (3) P_i keeps the first half of it and throws away the second one, whereas P_j does the opposite.
  • (1) P_i sends its subsequence to P_j, (2) P_j does the merging and (3) returns the first half of the result to P_i.
  For a network with duplex links, the first method is clearly faster even if the number of computational steps is double, but asymptotically, both are equivalent.

  Since CE and CS sorting differs just in the granularity of the basic step of sorting, we will for the sake of simplicity always assume than p=N. In practice, however, we have always p<< N, so we will always investigate scalability. It should be noted here that sorting algorithms have extremely large isoefficiency functions.

Lemma

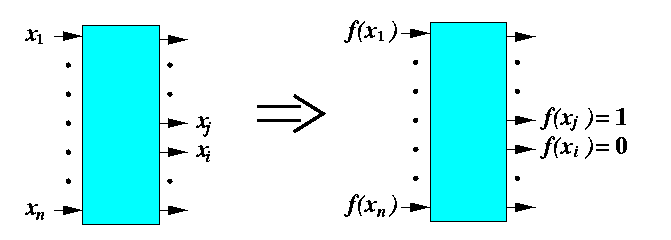
Let f be a monotonically increasing function on a linearly ordered set S, i.e.,

for all  x,y in  S; x<= y iff f(y)<= f(y).

If a comparator network transforms an input sequence X=x₁,...,x_n of elements from S into an output sequence Y=y₁,...,y_n, then it transforms the input sequence f(X)=f(x₁),...,f(x_n) into the output sequence f(Y)=f(y₁),...,f(y_n).

1. A single comparator is oblivious to f.
   • Consider a comparator with input values x and y.
   • Then its upper output will be min(x,y) and lower output max(x,y).
   • If we apply inputs f(x) and f(y), we will get min(f(x),f(y)) on the upper output and max(f(x),f(y)) on the lower output.
   • Since f is monotonically increasing, x<= y implies f(x)<= f(y).
   • But this implies that min(f(x),f(y))=f(min(x,y)) and max(f(x),f(y))=f(max(x,y)).
   

   CAPTION: Proof that one comparator is oblivious to any monotonically increasing function f.

   Hence, we have shown that

   for x,y in S, a comparator exchanges f(x) and f(y) iff it exchanges x and y.
2. Induction step. Using induction on the depth of the network, we can prove even a stronger statement than is the lemma: If a wire in the network carries value x_i when the input sequence is X, then it carries value f(x_i) when the input is f(X).
   • Basis of induction (trivial): If an input wire at depth 0 carries x_i, then it carries f(x_i) after applying f(X) to the network.
   • The induction step:
     • Assume that the induction hypothesis holds for all wires of depth d-1, d>= 1.
     • Take any wire of depth d. It is an output wire of a comparator whose input wires are at depth strictly less than d.
     • By induction hypothesis, if these input wires carry x_i and x_j when the input sequence X is applied, then they must carry f(x_i) and f(x_j) when f(X) is applied.
     • Since the comparator is oblivious to f, its output wires will carry f(min(x_i,y_j)) and f(max(x_i,y_j)).
     • But the same output wires carried min(x_i,y_j) and max(x_i,y_j) when the input sequence X was applied.

Lemma

(The 0-1 Sorting Lemma.) If a comparison network with N inputs sorts all 2^N possible sequences of 0's and 1's correctly, then it sorts all input sequences of arbitrary numbers correctly.

• Assume that the network sorts all zero-one sequences, but there exists a sequence X=x₁,...,x_n of arbitrary numbers such that the network fails to sort it correctly.
• This means that the input sequence contains two input numbers x_i and x_j, x_i < x_j, that the network places in wrong order on the output wires, i.e., x_j is placed before x_i in the output sequence.
• Let us define function f by

  f(z)= 0  if z<= xi
        1  if z > xi
  

• Then f is clearly monotonically increasing.
• Since the network places x_j before x_i in the output sequence when input X is applied, it follows from Lemma that it places f(x_j)=1 before f(x_i)=0 when the input sequence f(X) is applied.
• But f(X) is a zero-one sequence --- a contradiction.

CAPTION: A failure to sort X leads to a failure to sort a binary sequence.

Back to the beginning of the page	Back to the CS838 class schedule

Mesh-based oblivious sorting

for j=1...[ N/2] do_sequentially
     begin
       for i=1,3,..,2[ N/2]-1 do_in_parallel
           if xi > xi+1 then CE(xi,xi+1);
       for i=2,4,..,2[ (N-1)/2] do_in_parallel
           if xi > xi+1 then CE(xi,xi+1);
  end

Lemma

Even-odd transposition algorithm sorts N numbers on M(N) in N steps.

• The rightmost 1 has only 0's on its right hand, so it starts moving to the right at latest in the second step and keeps moving without interruption until it reaches its final position.
• The second rightmost element starts moving at latest in the third step, and proceeds similarly.
• Finally, the k-th rightmost 1 starts moving in (k+1)-th step to reach position N-k+1.
• Therefore, in the worst case, the total number of steps is k+(N-k)=N.

T(N,p)=\Theta((N/p)log(N/p))+\Theta(N).

• the parallel time is \Omega(N),
• the parallel time is O(N) only if p=\Omega(log N),
• E(N,p)=O(1) only if p=O(log N).

for i=1,..., 2log n+1 do_sequentially
  if (i is odd) 
        then SORT_ALL_ROWS_SNAKELIKE ( Figure, Phase 1,3,5)
        else SORT_ALL_COLUMNS ( Figure, Phase 2,4)

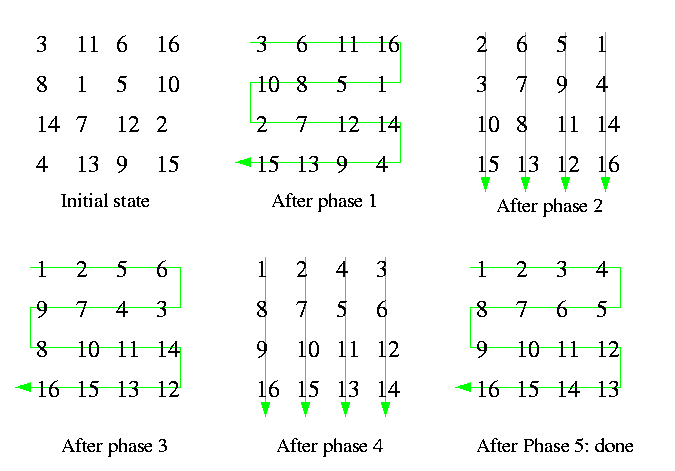
CAPTION: Five phases of ShearSort on M(4,4).

Shearsort on M(n,m) consists of 2log n+1 phases. In odd-numbered phases, individual rows are sorted alternately rightward and leftward. In even-numbered phases, individual columns are sorted downward. In both cases, we can use even-odd transposition sorting. Figure shows five phases of ShearSort on M(4,4).

Lemma

ShearSort needs [log n]+1 row phases and [log n] column phases to sort nm numbers on M(n,m) in a snakelike order.One row (column) phase takes \Theta(n) (\Theta(m), respectively) computational and communication steps.

• Assume any zero-one n× m matrix. It may contain rows of three kinds.
  1. all-one rows containing only 1's,
  2. all-zero rows containing only 0's,
  3. dirty rows containing both 0's and 1's.
• Initially, the input matrix can contain n dirty rows in the worst case.
• The final matrix sorted snakelike contains at most one dirty row.
• Proposition: One row and one column phase reduce the number of dirty rows to at least one half.
  Proof. By a simple case analysis. Consider all dirty rows after one row phase. One half of them is sorted rightward, whereas the other half reversely. If we consider pairs of leftward and rightward rows, there can exist pairs of at most three different types, as shown on Figure .
  

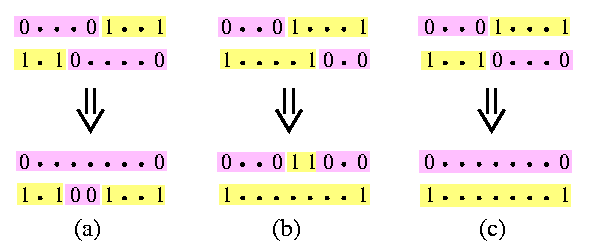
  CAPTION: Three kinds of pairs of dirty rows.

  After applying one column phase, one dirty row disappears in cases (a) and (b), and both dirty rows disappear in case (c).

• Hence, after 2log n phases, at most one dirty row remains and one more row sort completes sorting.

Lemma

Any oblivious snakelike sorting on mesh M(n,n) requires at least 3n-2\sqrt(n)-4 CE steps.

• Partition M(n,n) into the upper left triangular region R with sides 2\sqrt(n)× 2\sqrt(n) (i.e., comprising of 2n nodes) and the rest of the mesh, called region S.
• Consider the following input data:
  • each node in region S holds initially an arbitrary number from set {1,...,N-1},
  • each node in region R holds either 0 or N.
  

  CAPTION: Initial configuration of input data on M(n,n).

• Let r be the contents of the lower right corner node in step 2n-2\sqrt(n)-3 of A (see Figure ).
• Since the distance between this corner and any node in region R is 2n-2\sqrt(n)-2, the value of r could not be affected by any number initially located in region R, i.e., r is independent on whatever the contents of R initially was.
• For 0<= q<= 2n, let C(q) be the correct column for r if R contains initially q 0's and 2n-q N's.
• Note that in a row-major snakelike ordering starting in the upper left corner, the tail of the snake is either in the left or right lower corner of the mesh, depending on the parity of n.
• As we vary q between 0 and 2n, the value of C(q) varies between 1 and n, achieving each possible value between 1 and n at least twice.
• Therefore, for n odd or even, we can always find q' such that C(q')=1.
• It follows that by a suitable choice of input values, we can always force algorithm A to perform at least n-1 steps after its step 2n-2\sqrt(n)-3.

Phase 1.  sort all xz-planes in zx-order;
Phase 2.  sort all yz-planes in zy-order;
Phase 3.  sort all xy-planes in yx-order snakelike (in direction y);
Phase 4.  perform one odd-even and one even-odd transposition within all columns in parallel;
Phase 5.  sort all xy-planes in yx-order.

Proof
(by 0-1 Sorting Lemma) Consider any input sequence of 0's and 1's.

• After Phase 1, in every xz-plane, there is at most one dirty row and therefore:
  • any two yz-planes can differ in at most n 0's,
  • and all n yz-planes contain in their dirty rows at most n² elements.
• Therefore, after Phase 2, all dirty rows can span at most 2 xy-plane.
• If the dirty xy-plane is just one, we can go directly to Phase 5 and we are done,
• If there are 2 dirty xy-planes, Phases 3 and 4 eliminate at least one of them and Phase 5 completes the sorting.

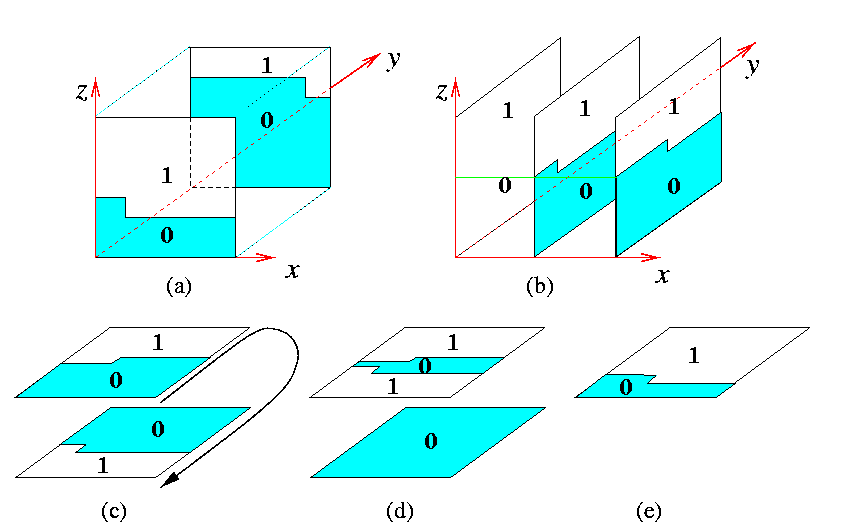
CAPTION: 3-D mesh lexicographic sorting.

Back to the beginning of the page	Back to the CS838 class schedule