| Back to the beginning of the page | Back to the CS838 class schedule |

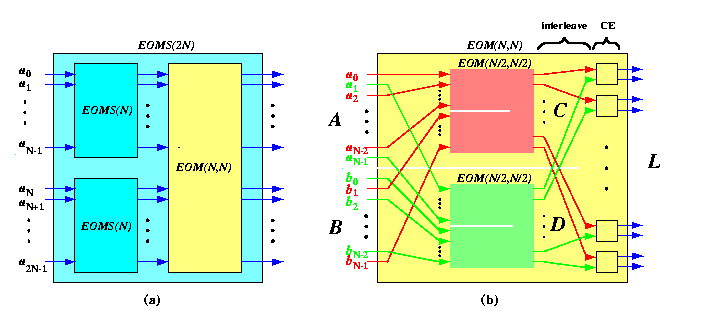
CAPTION: The structure of Even-Odd MergeSort (a) and Merge (b) network.
Functional description of the EOMS algorithm implemented by the network on Figure (a) is then
{EOMergeSort}(a0,...,a2N-1)=
{EOMerge}({EOMergeSort}(a0,...,aN-1),{EOMergeSort}(aN,...,a2N-1)).
Clearly, the key trick of the EOMS algorithm is hidden in the structure of the merge network. It turns out that it can also be constructed recursively!!!
Consider two sorted sequences A=a0,a1,..,aN-1 and B=b0,b1,..,bN-1. The sorted sequence L={EOMerge}(A,B) of length 2N can be constructed as follows:
even(A)=a0,a2,..,aN-2odd(A)=a1,a3,..,aN-1 even(B)=b0,b2,..,bN-2 odd(B)=b1,b3,..,bN-1 Note that since A and B are sorted, so are their odd and even subsequences. - Recursively,
- merge even(A) with odd(B) into a sorted sequence C=c0,c1,..,cN-1,
- merge odd(A) with even(B) into a sorted sequence D=d0,d1,..,dN-1.
- Interleave C and D to form a sequence L'=c0,d0,c1,d1,..,cN-1,dN-1 (see the last stage in Figure (b)).
- Apply compare-and-exchange to each pair ci,di. The resulting Even-Odd Merge network is depicted in Figure (b). Its functional specification is as follows:
The main trick of this merge algorithm was discovered first by Batcher: to merge A and B, we just need to interleave C and D and we are almost done. Formally, it can be proven as follows.
C={EOMerge}(even(A),odd(B)) D={EOMerge}(odd(A),even(B)) L'={Interleave}(C,D) L={EOMerge}(A,B)={Pairwise_CE}(L') Lemma
Even-Odd Merge algorithm merges 2 sorted sequences of length N into a sorted sequence of length 2N in log N+1 parallel CE steps using N(log N+1) comparators.Proof
(By 0-1 Sorting Lemma.) The lemma obviously holds for N=1. Let N=2k, k>= 1.Let us prove the complexity. Let dm(2N) be the depth of EOM(N,N). For N=1, we can do the merge using one comparator, hence dm(2)=1. Since EOM(N,N) is recursive and each level of recursion adds just one column of comparators, we have dm(2N)=dm(N)+1 which gives dm(2N)=log N+1=log(2N). The number of comparators of M(N,N) is cm(2N)=Ndm(2N)=Nlog(2N).
- Consider two sorted binary sequences A and B of equal length N.
- Assume that A consists of \alpha 0's followed by N-\alpha 1's and B consists of \beta 0's followed by N-\beta 1's.
- Then the sequence C={EOMerge}(even(A),odd(B)) has \gamma=[\alpha/2]+[\beta/2] 0's, whereas the sequence D={EOMerge}(odd(A),even(B)) has \delta=[\alpha/2]+[\beta/2] 0's (see Figure ).
- Since |\gamma-\delta|<= 1, it follows that
the number of 0's in C and D can differ by at most one. CAPTION: The proof of correctness of EOMS using the 0-1 Sorting Lemma.
- So, if we form L'={Interleave}(C,D)=c0,d0,c1,d1,..,cN-1,dN-1, only three cases can occur.
- (a)\gamma-\delta=1. Then C has one additional zero compared to D and L' is already sorted.
- (b) \gamma-\delta=0. Then C and D have exactly the same number of 0's and L' is sorted as well.
- (c) \gamma-\delta=-1. Then the number of 0's in C is by one less than in D and we get only one incorrectly sorted pair (c\gamma,d\gamma)=(1,0) in L'. By applying the compare-and-exchange operation to this pair, we get a sorted sequence L.
And the overall complexity of EOMS easily follows.
Lemma
EOMS sorts N numbers in O(log2N) parallel CE steps using O(Nlog2N) comparators.Proof
Let ds(N) denote the depth of EOMS(N) ( Figure (a)). Then ds(2)=1 and ds(2N)=ds(N)+dm(2N). Since dm(N)=log N, it follows that ds(N)=log N(log N+1)/2. For the number of comparators cs(N), we have similarly cs(2)=1 and cs(2N)=2cs(N)+cm(2N) which gives cs(N)=Nds(N)/2=O(Nlog2N).CAPTION: Unfolded Even-Odd Merge Sorting network. The numbers denote the depth of the corresponding Merge network. In all stages, the subsequences are sorted monotonically.
Back to the beginning of the page Back to the CS838 class schedule Even-Even MergeSort
There exists another slightly modified merging scheme which is equivalent to EOMS in terms of the main idea and performance. It is called Even-Even MergeSort (EEMS). It differs from EOMS in just two details.Figure illustrates the structure and the way it differs from the Even-Odd MergeSort network. The functional specification of the Even-Even Merge network is therefore.
- EEMS merges recursively
- even(A) with even(B) to produce C
- odd(A) with odd(B) to produce D
- The final CE operation does not touch the first element c0 and the last element dN-1 (since c0 is always the least and dN-1 always the greatest number) and compares only odd-even pairs di,ci+1 for i=0,...,N-2.
C={EEMerge}(even(A),even(B)) D={EEMerge}(odd(A),odd(B)) {EEMerge}(A,B)={Pairwise_CE}({Even_Odd_Interleave}(C,D)) {EEMergeSort}(a0,...,a2N-1)={EEMerge}({EEMergeSort}(a0,...,aN-1),{EEMergeSort}(aN,...,a2N-1)) CAPTION: The structure of Even-Even MergeSort (a) and Merge (b) network.
Back to the beginning of the page Back to the CS838 class schedule Bitonic MergeSort
Bitonic Sort (BS) is yet another variant of MergeSort which has easier implementation on hypercubic networks. The parallel time and work complexity is the same as in EOMS. Instead of monotonically sorted sequences, BS works with bitonic sequences. A bitonic sequence has a valley and a peak.Definition
A sequence of numbers A=a0,a1,...,aN-1 is bitonic ifInstead of merging two ascending sequences of length N to produce an ascending sequence of length 2N, the basic operation used in Bitonic Sort is a merge of one ascending and one descending sequence, both of length N, into one ascending sequence of length 2N. It can be viewed as a transformation of a bitonic sequence into a monotonic one of the same length. This is called Bitonic Merge and its basic operation is called Bitonic Split.
- either there is an index i, 0<= i<= N-1, such that a0,...,ai is ascending and ai+1,...,aN-1 is descending,
- or there is a rotation of A such that the previous condition holds.
Definition
If A=a0,a1,...,a2N-1 is bitonic, defineThe following observation is of key importance.AL=min(a0,aN),min(a1,aN+1),...,min(aN-1,a2N-1)andAH=max(a0,aN),max(a1,aN+1),...,max(aN-1,a2N-1).Then the concatenation ALAH is called the bitonic split of A.Lemma
If A=a0,a1,...,a2N-1 is bitonic, thenProof
- AL and AH are again bitonic
- every number in AL is smaller than every number in AH.
Figure shows the Bitonic Split of A and the statement of the lemma easily follows from the figure.CAPTION: The Bitonic Split transforms one bitonic sequence A into two bitonic sequences. (a) Cutting A into left half A1 and right half A2. (b) Overlapping A1 with A2. (c) The Bitonic Split.
We can easily observe that if Bitonic Split is applied recursively to an input bitonic sequence A of length N, the sequence will become sorted into ascending order after log N steps. This is exactly what the Bitonic Merge, denoted by BM and depicted on Figure (b), does. The Bitonic Sort algorithm works similarly as EOMS, but it uses Bitonic Merge. Assume again that N is a power of two.
Figure shows again the recursive structure of the Bitonic MergeSort network and the Bitonic Merge network. BS{}+(N) denotes the Bitonic MergeSort network sorting sequences of length N in ascending order (BS{}-(N) sorts in descending order) and BM(N) denotes the Bitonic Merge network transforming bitonic sequences of length N into monotonic ones.
- The input unsorted sequence of 2N numbers is first split into N pairs.
- By passing through a comparator, each pair becomes a sorted sequence of length 2. However, the comparators in the first column are alternatively of ascending and descending type. Hence after the first step, every quadruple consists of an ascending and descending half, i.e., it forms a bitonic sequence of length 4.
- In the next step, Bitonic Merge networks of depth 2 transform bitonic sequences of length 4 into monotonic sequences so that again adjacent sequences are alternatively ascending and descending. This step produces bitonic sequences of length 8, and so on.
- Finally, the last Bitonic Merge network uses bitonic split to produce a monotonic sequence of length 2N form a bitonic one.
CAPTION: Recursive structure of Bitonic MergeSort (a) and the Bitonic Merge (b) networks.
The Bitonic Merge network on Figure (b) produces ascending sequences, but if we reverse the sense of ordering of all comparators, we get the descending case. Functionally, the networks can be specified as follows.
If we unfold the bitonic-merge stages, we again get a cascade of comparator stages of growing depth, so that the parallel time and cost is the same as in EOMS.
(ALAH)={Bitonic_Split}(A) {BMerge}(A)={BMerge}(AL){BMerge}(AH) {BSort+}(a0,...,a2N-1)={BMerge}({BSort+}(a0,...,aN-1){BSort-}(aN,...,a2N-1)) CAPTION: Unfolded Bitonic Sorting network.
Back to the beginning of the page Back to the CS838 class schedule MergeSort algorithms in hypercubic networks
Implementation of Even-Odd MergeSort
EOMS of N=2n numbers can be nicely implemented on ordinary butterfly oBFn in O(n2) steps. The implementation exploits the recursive structure of the butterfly, precisely matching the requirements of the algorithm.CAPTION: Even-odd Merge operation of two sorted sequences A and B of length 4 implemented on oBF3.
Let us describe the butterfly implementation of the Even-Odd Merge of two sorted sequences.
- Assume an oBFn and two sorted sequences A and B of 2n-1 numbers.
- Initially, A is input into the upper half of column 0 of oBFn and B into the lower half.
- During the first step, the numbers are moved to column 1 using straight edges for A and cross edges for B.
- After the first step, we use recursion to form
- C by merging even(A) with odd(B) in the blue subbutterfly oBFn-1 induced by the even rows (the numbering of rows starts from zero from the top)
- D by merging odd(A) with even(B) in the red subbutterfly oBFn-1 induced by the odd rows.
- After the recursion has finished, the elements of C and D are located in nodes of column 1 of oBFn in the order c0,d0,c1,d1,.... oBFn arranges the elements of C and D so that they are interleaved and directly form the sequence L'!!!
- The final sequence L={EOMerge}(A,B) is produced by moving the data to nodes in column 0 of oBFn using straight or cross edges depending on whether the numbers ci and di are out-of-order or not.
CAPTION: Even-Odd MergeSort of 16 numbers on Q4.
If we unfold the recursion, we find out that data move in n steps forward and sequence B is reversed when it reaches the rightmost column, whereas sequence A gets there unchanged. During the backward n-step phase, the data use the cross edges whenever adjacent pairs are out of order. Analogously, Even-Odd Merge of sorted sequences of length 2k is implemented as exactly the same forth and back sweep of data through oBFn, but only using its first k stages. The implementation on an N-node hypercube is straightforward by contracting the rows of the ordinary butterfly into hypercube nodes, as shown on Figure . It is obvious that the hypercube implementation requires some extra steps after each merge operation to bring the corresponding even-odd subsequences into correct positions. A more detailed investigation reveals that basically
every other ascending subsequence is reversed into a descending one. But this is exactly what the Bitonic Sort does for free!!!!Implementation of Bitonic Sort
Bitonic Sort has almost the same implementation on the butterfly, adjacent butterflies just sort the corresponding subsequences alternatively as ascending and descending. But this means that in the hypercube, no extra permutation steps are needed and the number of parallel CE steps equals exactly the depth of the Bitonic Sort network (see Figure ). Note that the hypercube dimensions used by Bitonic Sort are used in the following order: 1, 2, 1, 3, 2, 1, 4, 3, 2, 1, ...CAPTION: Bitonic MergeSort of 16 numbers on Q4.
Bitonic MergeSort has a simple implementation on shuffle-based networks. This follows from that fact that it always compares numbers with indexes that differ by exactly one bit in their representation and corresponding pairs of numbers can be brought together by shuffle operation on the SE graph.
Back to the beginning of the page Back to the CS838 class schedule