Section#3: Parallel complexity theory - NC algorithms
(CS838: Topics in parallel computing, CS1221, Tue, Jan 26, 1999, 8:00-9:15 a.m.)

1. Basics notions of sequential complexity theory
2. Highly parallel feasibility
3. NC algorithms
4. Drawbacks of the class NC theory

Obviously, a sequentially intractable problem remains intractable in parallel if we use at most polynomial number of processors. And polynomial number of processors is the maximum we can hope for in practice. Hence, parallel complexity theory deals only with sequential polynomial problems. Most of the machinery of the parallel complexity theory is derived from the sequential one, which uses specific formal framework to make its results and conclusions independent on particular implementation details of algorithms and robust with respect to various models and architectures of computing devices. So before explain the basic ideas of the parallel complexity, we review the basic notions of the classical complexity theory, so that we can understand how the parallel complexity theory relates to the classical one.

Back to the beginning of the page	Back to the CS838 class schedule

Basics notions of sequential complexity theory

• Complexity class: a collection of problems of some characteristic worst cases difficulty. Some problems in a class may be easier than the others, but all of them can be solved within the same resource bounds associated with the class.
• Abstract problem: a binary relation between a set of problem instances and a set of the problem solutions. The size of an instance is the number of symbols (digits, letters, delimiters, etc) in the full problem specification.
  Example: SPP = Shortest Path Problem: Given graph G and two vertices u,v, find in G a shortest path between u and v. The set of instances is the set of all triples ( G,u,v) and a given instance may have zero, one, or more solutions - paths from u to v.
• Decision problem: a problem with solutions Yes/No. Optimization problems can be formulated as decision problems, typically by imposing bounds on the values to be optimized.
  Example: PATH = the decision problem for SPP: Given G, u,v and an integer k, does a path exist in G between u and v whose length is at most k?
• Observation: If a decision problem is hard, so is the related optimization problem (since easy optimization problem makes the decision problem easy). Therefore, the complexity theory deals only with decision problems. We will examine this in mode detail later!!
• Compact encoding: Any abstract notions, such as numbers, graphs, functions, polygons, programs, can be encoded using strings over some finite alphabet Z. An encoding is compact if the length of the encoded instance is of the same order as the size of the abstract instance. That is, they must be equivalent within a polynomial factor. This usually translates into the equirement that any value n must be encoded with O(log_m n) symbols of Z, where m=|Z|. Other obvious requirements on an encoding scheme are that it is must be easy to produce the encoding of any instance of the problem and that it may not produce more computational hints than any other encoding.
• Concrete problem: an abstract problem encoded for a computing device using some compact encoding, typically a binary one (such as ASCII).
• Input size: the length of a binary encoding of a problem instance, denoted by |x| for input x.
  Example: A graph G on n vertices can be encoded by an adjacency matrix of n² bits, hence |G|=n².
• Sequential time: A sequential algorithm solves a concrete problem in time T(n) if it produces a solution in time O(T(|x|)) for any input x.
• Polynomial class P: the set of all problems with T(n)=O(n^O(1)). A polynomial problem remains polynomial regardless of which ``compact'' encoding is chosen, since any such encoding can be converted into a binary one in polynomial time. That is why the complexity theory deals only with binary encoding.
• Binary language: a subset of binary strings. Any decision problem Q can be viewed as a language
  L<sub>Q</sub>={x in {0,1}<sup>*</sup>; Q(x)=1} of ``yes'' instances.
  Example: L_PATH: {( G,u,v,k); G is a graph with vertices V, u,v in V, k>= 0 is an integer, and there is a path between u and v in G whose length is at most k}.
• Input accepted/rejected by an algorithm: Algorithm A accepts (rejects) binary string x if A outputs 1 (0) for input x.
• Acceptability: L is accepted in time T(n) if any x in L is accepted in time T(n). To accept a language, the algorithm needs only to worry about strings in the language. If x is not accepted, then it is either rejected or A may loop forever for input x.
• Characteristic function of language L: function f_L:{0,1}^*->{0,1} such that f_L(x)=1 if x in L and f_L(x)=0 otherwise.
• Decidability: Language L is decidable in sequential time T(n) iff f_L is computable in O(T(n)) time. (Hence, if there is an algorithm which accepts every string x in L and rejects every x\not in L in time O(T(|x|))). There are problems such as Turing Halting Problem for which there is an accepting algorithm, but there is no deciding algorithm.
• Polynomial class P: the set of all languages decidable in sequential polynomial time.
• Verification algorithm: an algorithm A with arguments x and y where x is an ordinary input set and y is a certificate. A verifies x if there is a certificate y such that A(x,y)=1. The language verified by a verification algorithm A is L_A={x in {0,1}^*;\exists y in {0,1}^* such that A(x,y)=1}. If x\not in L_A, then there must be no certificate y such that A(x,y)=1.
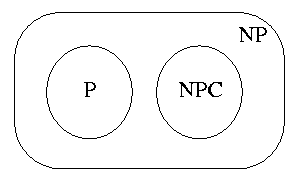
• Complexity class NP: the class of all languages that can be verified by polynomial-time verification algorithms. More precisely, L is in NP iff there is a verification algorithm A such that L={x in {0,1}^*; \exists certificate y such that |y|=O(|x|^O(1)) and A(x,y)=1}. (Historically, NP stands for nondeterministic polynomial).
  Example: Hamiltonian-cycle problem (HC): Given graph G, does it have a Hamiltonian cycle. No polynomial-time algorithm is known to decide HC. However, HC is in NP, since given a graph G and a permutation of its vertices, we can verify in polynomial time whether the permutation is a Hamiltonian cycle of G.

Famous open problem P\not=NP?

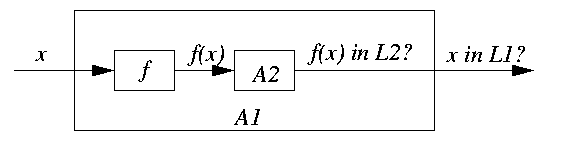
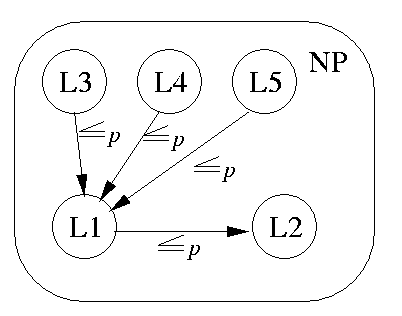
• Polynomial-time reduction: L₁ is polynomial-time reducible to L₂, L₁<=_pL₂, if there exists a polynomial-time function f:{0,1}^*-> {0,1}^* such that for all x in {0,1}^* (x in L₁ iff f(x) in L₂).
• NP-complete problem: L is NP-complete if L in NP and L'<=_pL for every L' in NP.

Lemma

Lemma

Corollary: If there exists an NP-complete problem such that is in P, then P=NP. If there exists an NP-complete problem which is proved not to be in P, then no NP-complete problem is in P. There is a strong evidence for the second case to be true. There are hundreds of NP-complete problems. To show that a language L is NP-complete, we have to show that L is in NP (which is usually easy) and then there are two choices:

• We show that any NP language can be reduced to L in polynomial time. This was necessary for the first NP-complete problems, such as CIRCUIT-SAT: ``Given a Boolean combinatorial circuit composed of AND, OR, and NOT gates, with inputs x₁, x₂, ..., x_n and designated output y, is there an input set such y is true?''
• If there exist already some NP-complete problems, then we
  1. select a suitable NP-complete L',
  2. given an algorithm that computes a function f mapping instances of L' into instances of L,
  3. prove that x in L' iff f(x) in L for all x in {0,1}^*,
  4. prove that f is in P.

• Parallel decidability: A language L is decided in parallel time T(n,p) with p(n) processors iff f_L is computable in parallel time T(n,p) with p(n) processors. By default, we assume PRAM computation.

Lemma

However, the goal of parallel computation is to achieve a highly parallel feasibility: to reduce the sequential polynomial complexity of problems to subpolynomial parallel time!!!! For that, we must use polynomial number of processors, since

p(n).T(n,p(n))>= SU(n).

1. ``Which polynomial number of processors is acceptable/affordable?'' In practice, the polynomial number of processors is meant to be linear or close.
2. ``Which subpolynomial time is achievable''? It turned out that almost all highly parallel feasible problems can achieve polylogarithmic parallel time.

Again, we may assume PRAM model, and as we have seen in the previous lecture, if some algorithm is in NC, it remains in NC regardless of which PRAM submodel we assume. More generally, the class NC is robust with respect to any other accepted model of parallel computation (Bollean circuit model, LogP, Parallel memory hierarchy model, etc). The class NC includes:

1. parallel prefix (scan) computation
2. parallel sorting and selection
3. matrix operations (matrix multiplication, solving special cases of systems of linear equations)
4. parallel tree contraction and expression evaluation
5. Euler tour technique and derived algorithms
6. parallel algorithms for connected components of graphs
7. parallel graph biconnectivity and triconnectivity
8. parallel algorithms for many problems in computational geometry
9. parallel string matching algorithms

All parallel algorithms included in this course are NC, so that we will see many examples in detail during the course.

On the other hand, there are many problems for which no NC algorithms are known. Within this theory, they are considered badly parallelizable and usually called inherently sequential. This is going to be discussed in the next lecture. But before that, we take a look on problems with the NC class theory.

Back to the beginning of the page	Back to the CS838 class schedule

Drawbacks of the class NC theory

1. The class NC may include some algorithms which are not efficiently parallelizable. The most infamous example is parallel binary search. The trouble is that this problem has polylogarithmic time complexity even for p(n)=1. If we apply p>1 processors, we get T(n,p)=log_p+1n and therefore the cost C(n,p)=(p/log p)log n and the speedup is S(n,p)=log(p+1) which is far from what could be considered as a highly parallel solution.

   Any sequential algorithm with logarithmic time is in NC regardless of its parallel feasibility!!!

2. NC theory assumes situations where a huge machine (polynomial number of processors, e.g., millions) solves very quickly (polylogarithmic time, e.g., seconds) moderately sized problems (e.g., hundred of thousands input items). In practice, however, moderately sized machines (hundreds, at most thousands of processors) are used to solve large problems (e.g., millions of input items). So that the number of processors tends to be subpolynomial, even sublinear.
3. Some problems in P have sublinear parallel time O(n^x), 0<x<1, and are not therefore in NC. But sublinear functions may be less progressive for practical values of n and the asymptotic behavior becomes relevant only for impractically large n. For example, \sqrt{n}<log³n for n<= 0.5 x 10⁹. So, sublinear parallel time algorithms may run faster than NC algorithms.

Last modified: Mon Jan 25 by Pavel Tvrdik