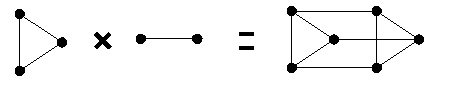Section#5: Direct interconnection networks I+II
(CS838: Topics in parallel computing, CS1221, Tue+Thu, Feb 2+4, 1999, 8:00-9:15 a.m.)

1. Basic notions and terminology
2. Requirements on interconnection networks
3. Mesh-based topologies
4. Hypercubic topologies
5. Tree-based topologies
6. Shuffle-based topologies

Back to the beginning of the page	Back to the CS838 class schedule

Basic notions and terminology

Alphabets and strings

d-ary alphabet

is denoted by Z_d={0,1,..,d-1}. The operation + modulo n is denoted by +_n.

n-letter d-ary strings

Z_dⁿ={x_n-1... x₀; x_i in Z_d}, n>= 1. The length of string x is denoted by len(x). The empty string (i.e., of length 0) is denoted by e. The i-fold concatenation of string x is denoted by xⁱ.

Binary alphabet

is denoted by B. The inversion of bit b_i is \non(b_i)=1-b₁. If b=b_n-1.. b_i+1b_ib_i-1.. b₀ in Bⁿ, then \non_i(b)=b_n-1.. b_i+1\non(b_i)b_i-1.. b₀.

Graph theory

Vertex and edge set

of graph G is denoted by V(G) and E(G), respectively. Two adjacent vertices u and v form edge ( u,v). They are incident with the edge. Edges ( u,v) and ( v,w) are adjacent.

H = subgraph

of G, H\subset G, if V(H)\subset V(G) and E(H)\subset E(G).

H = induced subgraph

of G if it is a maximal subgraph of G with vertices V(H).

H = spanning subgraph

of G if V(H)=V(G).

Union

of two disjoint graphs G₁ and G₂, G₁\cup G₂, is a graph with vertices V(G₁)\cup V(G₂) and edges E(G₁)\cup E(G₂).

Cartesian product

of G₁ and G₂ is graph G=G₁ x G₂ with V(G)={(x,y); x in V(G₁), y in V(G₂)} and E(G)={( (x₁,y),(x₂,y)); ( x₁,x₂) in E(G₁)}\cup {( (x,y₁),(x,y₂)); ( y₁,y₂) in E(G₂)}.

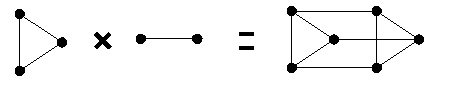
CAPTION: An example of a cartesian product

Degree of vertex

u, deg_G(u), is the number of neighbors of u.

Degree set of graph

G, deg(G), is the set {deg_G(u); u in V(G)}.

Maximum degree

of G is \triangle(G)=max(deg(G)).

Minimum degree

of G is \delta(G)=min(deg(G)).

k-regular graph

G has \triangle(G)=\delta(G)=k.

Connected graph

Every pair u, v of vertices is joined by a path P(u,v), a sequence of adjacent edges.

Path length

len(P(u,v)), is the number of edges P(u,v).

Distance

between vertices u and v, dist_G(u,v), is the length of a shortest path joining u and v.

Average distance

in G, dist_G(u,v), is \Sigma_u,vdist_G(u,v)/(N(N-1)).

Diameter

of G, diam(G), is the maximum distance between any two vertices of G.

Cycle

is a closed path.

Vertex-disjoint paths

P₁(u,v) and P₂(u,v) have no vertices in common except for u and v

Edge-disjoint paths

P₁(u,v) and P₂(u,v) have no edges in common.

Connectivity

(Vertex) connectivity of G, \kappa(G), is the minimum number of vertices whose removal results in a disconnected graph. Edge connectivity of G, \lambda(G), is the minimum number of edges whose removal results in a disconnected graph. It follows that

\kappa(G)<= \lambda(G)<=\delta(G).

CAPTION: Example of a graph G with \kappa(G)=1 and \lambda(G)=\delta(G)=2.

k-connected graph

has \kappa(G)=k. Similarly, k-edge-connected graph has \lambda(G)=k.

Optimal connectivity

\kappa(G)=\lambda(G)=\delta(G).

Menger's theorem

Between any two distinct vertices of G, there are at least \kappa(G) vertex-disjoint paths and at least \lambda(G) edge-disjoint paths.

Fault diameter

of a connected graph G is the maximum over the lengths of all the shortest vertex-disjoint paths between any two vertices in G. Similarly, we can define the fault distance between any two vertices.

Bipartite graph

There exists a bipartition (or 2-coloring) of its vertex set V, which is a partitioning of V into two disjoint subsets V₁ and V₂ such that each edge of G has one vertex in V₁ and the other vertex in V₂.

Balanced bipartite graph

has a bipartition (V₁,V₂) with |V₁|=|V₂|.

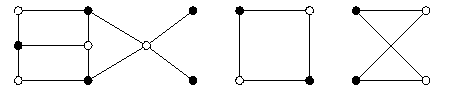
CAPTION: Examples of bipartite graphs, the first one is not balanced

Hamiltonian path/cycle

of a connected G is a path/cycle joining all vertices of G. A graph having a hamiltonian cycle is hamiltonian. A bipartite graph can have a hamiltonian cycle only if it is balanced.

(Edge) bisection width

of G, bw_e(G), is the smallest number of edges removal of which divides G into two parts of equal size (up to one vertex).

Vertex bisection width

of G, bw_v(G), is the smallest number of vertices removal of which divides G into two parts having at most [|V|/2] vertices each.

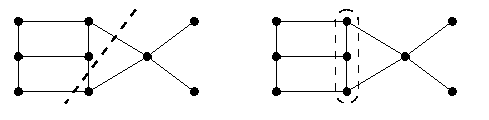
CAPTION: An example of a graph with both edge and vertex bisection width 3

Isomorphism

Two graphs are isomorphic if they can be made identical by relabeling vertices.

Automorphism

of G is any isomorphic mapping of G to itself.

Vertex-symmetric

graph looks the same independently of from which vertex you look at it, i.e., for any two distinct vertices u and v, there is an automorphism of the graph sending u to v.

Edge-symmetric

graph looks the same independently of from which edge you look at it, i.e., for any two distinct edges e₁ and e₂ in E(G), there is an automorphism of G sending e₁ to e₂. Graph G on Figure is edge symmetric, but it is not vertex symmetric. It becomes vertex symmetric if the vertices 1 and 3 are merged. A vertex symmetric graph must be regular.

Digraphs = Oriented graphs

A digraph G has arc set A(G). Arc ( u->v) is incident from u to v u,v in V(G). Vertex u (v) is incident from (to) arc ( u->v), respectively. Arcs ( u->v) and ( v->w) are adjacent. The in-degree and out-degree of u in V(G), denoted by \indeg_G(u) and \outdeg_G(u), is the number of arcs incident to and incident from u, respectively. The other notions are derived similarly, digraphs have oriented paths (dipaths), oriented diameters, strong connectedness, and strong connectivity.

Small diameter and small average distance

Small average distance allows small communication latency, especially for distance sensitive routing, such as store-and-forward. But it is also crucial for distance insensitive routing, such as wormhole routing, since short distances imply less used links and buffers, and therefore less communication contention.

Small and fixed vertex degree

Small and constant vertex degree allows simple and low-cost universal (i.e., independent of the network size) routers which amortizes the design costs. On the other hand, it implies less links and lower connectivity and larger distances. Ideally, we would like to get low constant vertex degree and at most logarithmic diameter simultaneously. Given N-vertex graph such that \triangle(G)<= k for some constant k, the number of vertices reachable in G within i steps from any vertex is O(kⁱ). Hence, N=O(k^diam(G)), which is equivalent to diam(G)=\Omega(log N). Fixed-degree networks cannot have better than logarithmic diameter.

Large bisection width

Many problems can be solved in parallel using binary divide-and-conquer: split the input data set into two halves and solve them recursively on both halves of the IN in parallel, and then merge the results in both halves into the final result. Small bisection width implies low bandwidth between both halves and it can slowdown the final merging phase. On the other hand, a large bisection width is undesirable for a VLSI design of the IN, since it implies a lot of extra chip wires.

High connectivity and fault tolerance

The network should provide alternative paths for delivering messages in case of link or node faults or communication congestions. Large packets can be delivered faster if they can be split into smaller chunks sent along disjoint paths.

Small fault average distance and diameter

To have these alternative or parallel disjoint paths as short as possible, small fault average distances and small fault diameter are naturally desirable.

Hamiltoniaty

The existence of at least a hamiltonian path is not the most important requirement, but it is useful whenever we need to label processors with numbers 1,...,p so that adjacent processors get successive numbers (for example in sorting algorithms).

Hierarchical recursivity

INs are usually defined using some independent parameters, called dimensions. The set of all graphs of different dimensions based on a given definition forms a topology. A topology is hierarchically recursive if a higher-dimensional graph contains lower-dimensional graphs with the same topology as subgraphs. Many INs used in parallel systems are hierarchically recursive, topologies based on cartesian product are one example. Recursiveness makes the design and technology of manufacturing INs easier. Large scale problems that can be solved in parallel by recursive decomposition into smaller subproblems can be easily and efficiently mapped on the hierarchically recursive topologies using induction.

Incremental extendability and incremental scalability

If the definition of the topology allows graphs of any size, the topology is said to be incrementally extendable. There are incrementally extendable topologies, and some are at least partially extendable, since they allow size granularity only greater than 1. Some hierarchically recursive topologies allow graphs of specific discrete sizes, such as powers of two. If a topology is incrementally extendable, a very important question is how the structure of an instance of size n differs from the structure of an instance of size n+k for some integer constant k>=1. An (n+k)-vertex instance can be obtained from a n-vertex one by removing r(k) edges (to get a subgraph of the larger instance) and by adding additional vertices and corresponding edges to this subgraph. If r(k)=O(k), the topology is said incrementally scalable. Very few topologies are incrementally scalable. For example, 2-D meshes are incrementally extendable, but not scalable.

Symmetry

This is a very important requirement. Many IN topologies are vertex or edge symmetric. Intuitively, a symmetric network is easy to understand and the design of parallel and communication algorithms is very much easier, since it is irrelevant where the computation and/or communication starts or in which directions it will evolve. Also, the symmetry is helpful for solving issues related to VLSI design.

Support for routing and collective communication

This is a crucially important property and we will devote it several lectures. The network topology should enable an simple shortest path routing, so that the basic routing algorithm could be implemented in hardware. Equally important parameters of an IN are complexities of permutation routing and one-to-all and all-to-all communication operations. The design of efficient communication algorithms is very simplified if the topology is symmetric and it also depends on the communication technology and router architecture.

Embeddability of and into other topologies

The efficiency of a parallel algorithm running on a parallel machine depends on the similarity between the process graph and the underlying physical IN topology. We need a suitable mapping or embedding of the process graph into the topology. Desirable are those topologies which are able to simulate efficiently other topologies.

Simple VLSI or 3-D layout

Any VLSI implementation of an IN implies VLSI-related requirements, such as easy mapping to rectangular grid, decomposition of a large IN into building blocks so that the lengths and numbers of inter-chip wires is minimal (recall the bisection width above). Except for the bisection width, the discussion of VLSI design issues is beyond the scope of this course.

Binary hypercube of dimension n, Q_n

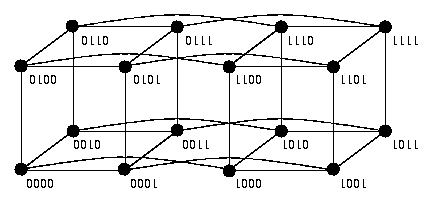
CAPTION: Hypercube Q₄

• The hypercube is a regular balanced bipartite hamiltonian graph.
• The distance between two vertices u and v in Q_n is the Hamming distance.
• It has logarithmic diameter. The average distance in Q_n is n/2.
• It is not a constant-degree topology, the vertex degree grows logarithmically with the number of vertices. If the number of nodes of a parallel computer doubles, the degree of each vertex increases by one. A router with k communication ports can be used for building a machine with at most 2^k nodes. This problem is solved by constant-degree and logarithmic-diameter derivatives of the hypercube, called hypercubic networks, see Page.
• The hypercube has the largest possible bisection width. Each vertex in one half is adjacent to its image in the other half.
• The connectivity of Q_n is n, which is optimal. If k<= n is the distance between vertices u and v, then there are n vertex-disjoint (therefore edge-disjoint) paths between u and v such that k of these paths have length k and n-k paths have length k+2.
• The fault diameter of Q_n is n. If we remove n-1 edges from Q_n, there still exists a path of length at most n between any two vertices.
• Fault tolerance is also excellent, there are k! different shortest paths between two vertices in distance k, since k! is the number of permutations of k coordinates in which the addresses differ.
• The hypercube is hierarchically recursive. Q_n is a cartesian product of subcubes:

  Qn=Qk x  Qn-k,  k in {1,...,n-1}.
  

  There are n\choosek ways how to make this decomposition. In particular, for any j in N there exists a canonical decomposition of Q_n into two (n-1)-cubes Q_n-1[j=0] and Q_n-1[j=1] (This gives the optimal bisection width.) For example, since Q₆=Q₃ x Q₃, we can view a Q₆ as a 3-cube, whose vertices are 3-cubes (Figure shows a simplified picture of that). But also Q₆=Q₂ x Q₄=Q₂ x Q₂ x Q₂, and so on. Each k-dimensional subcube S of Q_n is uniquely specified by its address s_n-1... s₁s₀, where s_i in {0,1,*}, with exactly k appearances of the don't care symbol *. 0-dimensional subcubes are vertices and subcubes are generalized ``internally structured" vertices. Vertices correspond to minterms and subcubes to terms in Boolean algebra.
• The hypercube topology is not incrementally extendable, it is defined only for powers of two. However, many incrementally extendable generalizations have been proposed, such as incomplete hypercubes.
• The hypercube is both vertex- and edge-symmetric graph. The automorphism group of Q_n consists of 2ⁿ x n! translations and rotations. A translation is a systematic renaming of vertices. Let \XOR denote the bitwise XOR operation. Translation from u to v is a mapping for all x in V(Q_n) (x-> (u\XOR v)). A rotation is a permutation (renaming) of dimensions.
• The basic routing algorithm is trivial and optimal, usually hardwired, and called e-cube routing: The bits in which the sender and receiver differ are compared in a fixed order, usually left to right.
• There exist optimal algorithms for collective communication in almost all communication models.
• The hypercube can also simulate efficiently almost any other topology.

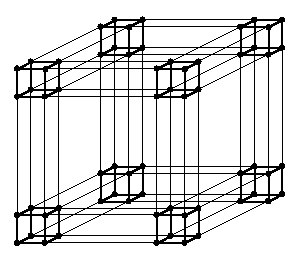
CAPTION: Q₆=Q₃ x Q₃.
The notion of subcubes is extremely important for using a hypercube multiprocessor as a multiuser multitasking machine. Users declare the numbers of required nodes for their tasks and the operating system allocates, if possible, subcubes of the appropriate size, which are released upon completion of the tasks. This is called the subcube allocation problem and there exist many algorithms for it which must maintain lists of allocated and free subcubes. Dynamic allocation and releasing of subcubes lead to the fragmentation problem in the hypercube similar to segment fragmentation of dynamic or virtual memory. The hypercube is the best topology for implementing most parallel and communication algorithms. It serves as a testbed for parallel feasibility of problems on distributed memory architectures. Its only drawback is the logarithmic vertex degree and lack of scalability. Several families of older massively parallel multiprocessors were based on the hypercube: nCUBE series 1 and 2, Intel's iPSC/2 and iPSC/860, TMC's CM-2, and several others. Currently, SGI Origin's interconnection network uses hypercube topology.

n-dimensional mesh of dimensions z₁,z₂,..,z_n, M(z₁,z₂,..,z_n)

• When dealing with a mesh, we usually assume that its dimension n is fixed. If we want to change its size, we change the side lengths. All the properties explained in what follows are stated under the assumption of fixed mesh dimension.
• The most practical meshes are, of course, 2-D and 3-D ones: they have trivial VLSI or 3-D design (2-D meshes are planar) and allow simple and natural mapping of 2-D and 3-D space problems with locality of interprocessor interactions (computer graphics and virtual reality, fluid mechanics, modeling of 3-D systems in earth sciences or astronomy, etc). They are also natural, even though not optimal, topologies for linear algebra problems (parallel solvers of linear or differential equations). 1-D meshes are called linear arrays and they are incrementally scalable.
• The mesh M(k,k,..,k) is called k-ary n-cube.
• A mesh is a bipartite (not necessarily balanced) graph. If at least one side has even length, the mesh has a hamiltonian cycle. A hamiltonian path exists always.
• Meshes are not regular, but the degree of any vertex is bounded by 2n. Of course, the degree of a corner vertex is less than the degree of an internal vertex.
• Therefore, meshes are not vertex symmetric. This complicates the design of some parallel and communication algorithms, but on the other hand, there are problems taking advantage of the asymmetry between boundary and internal vertices, e.g., parallel finite difference schemes for solving differential equations in 2-D and 3-D space.
• The distance between two vertices is the sum of differences in corresponding coordinates.
• The diameter is n-th root of the size of graph. It is large for lower-dimensional meshes, and therefore, they are not optimal for algorithms with global interactions, e.g., parallel sorting, or problems where global broadcasting or permutations are required, such as in parallel solvers of linear equations. So, 2-D or 3-D mesh are simple extendable INs with small fixed vertex degree.
• The exact value of bisection width is known only if max_iz_i is even. Then removing the middle edges of linear paths in the longest-side direction results in a bisection of minimal size. However, if max_iz_i is odd, the exact value of the bisection width is not known for n>= 4. However, it is easy to calculate it for 2- or 3-D meshes. For example, bw_e(M(11,9,6))=64. (Can you show that?) Lower-dimensional meshes have very low bisection width, which creates a bottleneck for many parallel mesh-based algorithms.
• The connectivity is optimal. The proof is similar to that for hypercubes. Also, the shortest path redundancy is optimal.
• The fault diameter is optimal, equal to the nonfaulty diameter. Fault distances are by at most 4 larger than nonfaulty ones.
• Meshes are also hierarchically recursive. They can be decomposed into cartesian products of lower-dimensional meshes, up to the canonical decomposition into a cartesian product of linear arrays: M(z₁,z₂,..,z_n)=M(z₁,z₂,.., z_n-1) x M(z_n)=M(z₁,..,z_i) x M(z_i+1,..,z_j) x M(z_j+1,..,z_n)=M(z₁) x M(z₂) x ... x M(z_n). Submeshes are also denoted by strings with don't-care symbols.
• Meshes are incrementally extendable, but not incrementally scalable. You can define a mesh of any size, but the amount of edges that must be removed from a smaller one to construct a larger one, can be very large.
• The basic shortest-path routing in general meshes is also trivial. It is called dimension ordered routing. Again, addresses of the sender and receiver are inspected in a prespecified order and the message is sent via the first port corresponding to a coordinate in which the addresses differ. In 2- and 3-D meshes, this is called XY and XYZ routing.
• Many optimal communication and parallel algorithms have been developed for meshes (optimal in the sense of matching the mesh lower bounds due to large diameter, low bisection width, etc), namely for 2-D and 3-D meshes. Many of them will be treated in detail in this course.
• Besides standard meshes, various modifications have been proposed, such reconfigurable meshes, meshes of buses, and so on. We will not deal with these variants here.

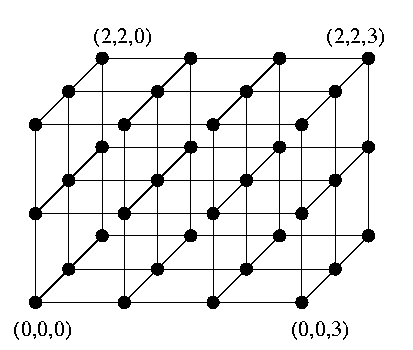
CAPTION: Mesh M(3,3,4)

n-dimensional torus of dimensions z₁,z₂,..,z_n, T(z₁,z₂,..,z_n)

• A 1-dimensional torus is simply a cycle or ring.
• The torus T(k,k,..,k) is called k-ary n-torus.
• Tori are bipartite iff all side lengths are even. But then, they are balanced.
• Any torus has a hamiltonian cycle.
• Tori are regular and vertex symmetric. The automorphism group consists of translations. k-ary n-tori are also edge symmetric and have rotations as automorphisms.
• The diameter and average distance of a torus drops to nearly one half compared to a mesh with the same dimensionality, and the connectivity and the bisection width doubles. Hence, the connectivity of n-dimensional torus, 2n, is also optimal.
• They are also hierarchically recursive, again thanks to cartesian product structure. Each torus can be canonically decomposed into a cartesian product of cycles.
• Scalability properties are even slightly worse here than at meshes.
• Cyclic structure of tori makes shortest path routing algorithms more complicated, but the basic approach remains dimension ordered routing.
• Similarly to meshes, many fundamental problems are known to have topologically optimal solutions on tori and we will demonstrate many of them here.

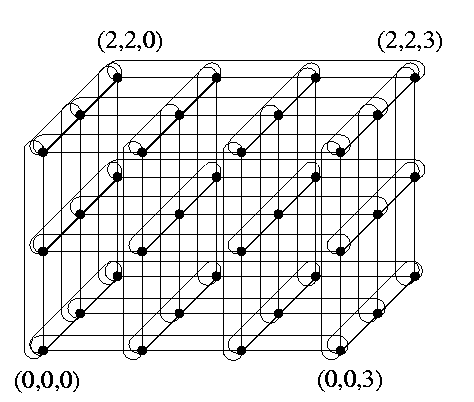
CAPTION: Torus T(3,3,4).

Comparisons of hypercubes, meshes, and tori

• M(2,2,..,2) is isomorphic Q_n
• n-dimensional meshes and tori are generalizations of Q_n
• For some k and n, k<n, a k-dimensional mesh/torus can be a subgraph of Q_n.

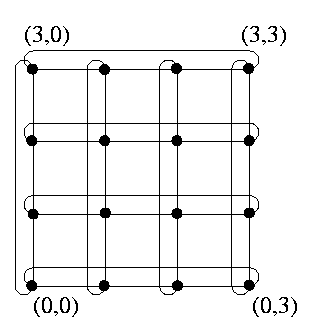
CAPTION: T(4,4)= Q₄.
Table shows the tradeoff between the diameter, number of edges, and bisection width of M(8,8,4), T(8,8,4), and Q₈. All these graphs have the same size |V()|=256 and M(8,8,4)\subset T(8,8,4)\subset Q₈.

Cube-connected cycles of dimension n, CCC_n

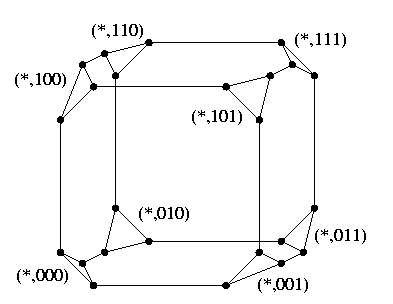
CAPTION: Cube Connected Cycles CCC₃.

• CCC_n is balanced bipartite iff n is even.
• Any CCC_n has a hamiltonian cycle.
• CCC is a regular and vertex-symmetric topology. Figure(b) shows it clearly. It is not an edge-symmetric graph, there are two kinds of edges: hypercube edges and cycle edges.
• It has optimal connectivity 3. Between two arbitrary vertices, there are at most two shortest paths.
• Shortest path routing is based on e-cube routing and Figure(b) is helpful in understanding it.
• In contrast to the hypercube, CCC is not hierarchically recursive. We can split a CCC_n into two halves which are very similar to CCC_n-1, but they have one abundant vertex in each cycle.

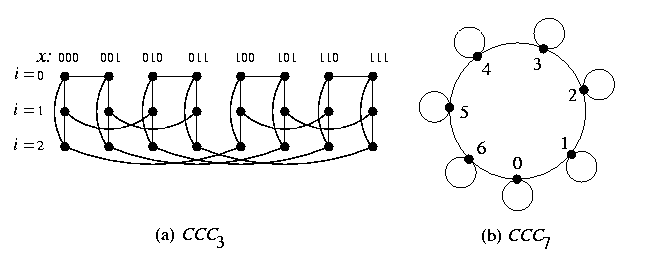
CAPTION: Another view of CCC.

Butterfly of dimension n

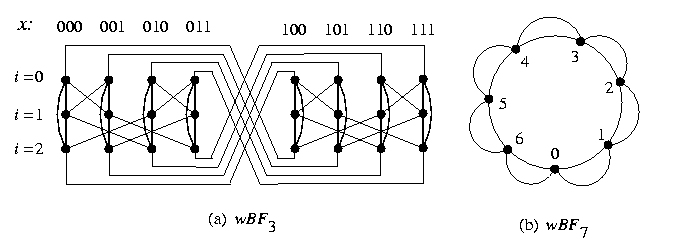
CAPTION: Wrapped butterflies
An n-dimensional ordinary butterfly, oBF_n, can be made form wBF_n by replacing n-vertex cycles with (n+1)-vertex paths (or in other words, an ordinary butterfly is a hypercube with each vertex unfolded into a path).

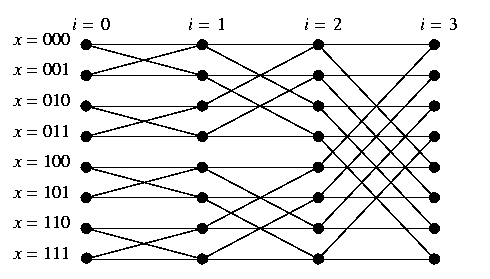
CAPTION: Ordinary butterfly oBF₃.

• The vertices of oBF_n are organized into columns (stages) i, 0<= i<= n, and rows x, 0<= x<= 2ⁿ-1. There are also two kinds of edges in the ordinary butterfly: straight edges and cross (hypercube) edges (see Figure). Edges linking vertices of stages i and i+1 are said to be of stage i.
• The ordinary butterfly is not vertex symmetric, it is not even regular.
• It is not hamiltonian.
• On the other hand, it is hierarchically recursive: oBF_n contains two oBF_n-1 as subgraphs.
• The connectivity is 2, which is optimal.
• There exists only one shortest path between any pair of vertices (0,x) and (n,y). The path traverses each stage exactly once using a cross edge of stage i iff the row numbers x and y differ in the i-th bit. It follows that the basic shortest-path routing is basically the e-cube routing from hypercubes, see Page.

2-D mesh of trees of height n, MT_n

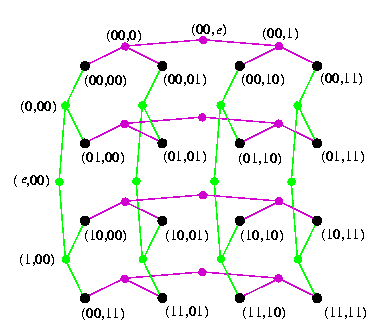
CAPTION: Mesh of trees MT₂.

• The mesh-of-trees topology can be defined for any mesh M(2^k,2^l). It can be even defined for any n-dimensional mesh with side lengths equal to powers of two. We will discuss only the 2-D square case for simplicity.
• Informally, a mesh-of-trees is a 2-D mesh whose linear rows and columns are replaced with row and column complete binary trees of height n, CBT_n. The original mesh vertices are leaves in the intersections of the row and column trees and the additional vertices are exactly the internal vertices of the trees. It follows that MT_n\subsetCBT_n x CBT_n.
• An N-vertex mesh-of-trees is constant vertex degree O(log N)-diameter and \Omega(\sqrtN)-bisection width topology.
• The mesh-of-trees topology is bipartite, but not balanced, therefore it is not hamiltonian.
• It is hierarchically recursive. By removing row- or column-tree roots, it decomposes into disjoint submeshes-of-trees. Low-level submeshes-of-trees can be used for local computations and the root nodes can be used for global communication and coordination.
• It is neither regular neither vertex symmetric.
• Its extendability is rather poor.
• Shortest-path routing is simple, it alternates routing in 2-D meshes and trees. Assume source vertex u and destination vertex v.
  • If u is in a row tree and v in a column tree, the shortest path from u to v is uniquely defined via the intersection leaf of both trees.
  • If u and v are in two different row trees T_u and T_v, compare the level of u and v in their trees. If u is lower than v, then go down in T_u to any leaf in the subtree, use the corresponding column tree to get to T_v, and use the tree routing in T_v to get to v (hence pass through the root of the smallest common subtree of v and of the homothetic image of u in T_v). If u is higher than v, then go first to the image of v in T_u and via any leaf get to T_v then. The number of different shortest paths depends on the heights of the vertices.
  • The routing between two internal nodes of column trees is similar.

• Logarithmic diameter and constant vertex degree.
• Optimal or nearly optimal connectivity.
• Fault diameter nearly the same as non faulty one, similarly for fault average distances.
• Large bisection width of order N/log N.
• Simple shortest-path routing.
• They are neither symmetric nor hierarchically recursive.
• They are rich of cycles of various lengths, since the rotation induces equivalence classes of vertices called necklaces.
• At the same time, they are rich of subtrees and spanning trees, since the general shift operation induces subtrees.

Shuffle-exchange networks

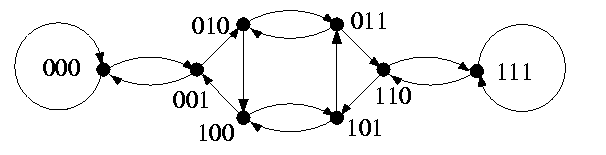
CAPTION: Digraph SE₃.

• ( x->\sigma(x)) is called a shuffle arc and ( x->\non₀(x)) is called an exchange arc.
• The distance between vertices 0ⁿ and 1ⁿ is 2n-1: we need n exchange and n-1 shuffle operations. The shortest dipath from vertex u to vertex v is constructed by finding the longest substring \alpha such that u=u'\alpha and v=\alpha v' and then by traversing the shuffle and/or exchange arcs so that prefix u' is converted into postfix v'. We need at most 2n-1 steps, which gives the diameter of SE_n.
• SE_n is a 2-regular digraph.
• The length of necklaces depends on the periodicity of strings. For example, if n=6, then the necklace containing vertex 111010 has length 6, whereas the necklace containing vertex 101101 has length 3. In general, the necklaces can have length i where i divides n. Therefore, the neighborhood of a vertex in a SE digraph depends on its periodicity and the SE topology is not vertex symmetric.
• Due to this necklace structure, digraph SE_n does not contain as subgraphs any SE_i, i<n. Fortunately, there exists so called ``approximate'' hierarchical recursivity of shuffle-exchange topology, as we will explain in further sections.
• The exact value of bw_e(SE_n) is known up to a small constant multiplicative factor.
• Undirected shuffle-exchange topology is similar. Strings can be rotated to the right, which is so called unshuffle operation \sigma^-1(x). The average distance drops, since unshuflle operation may provide shorter paths. For example, if n=10, u=1011101010, and v=1000010111, the shortest directed path from u to v has length 13, whereas the shortest undirected path has length 8. The diameter, bisection width, the number and lengths of necklaces remain the same. The shuffle-exchange graph is not regular.

De Bruijn digraph of degree d and dimension n, dB_d,n

• Vertex u of dB_d,n is adjacent to vertex v if the first n-1 letters of v equal to the last n-1 letters of u.
• Any vertex can be obtained from another one by at most n left shifts, hence the diameter. The fact that de Bruijn topologies have extremely low diameter is jeopardized by the fact that the average distance is very close to the diameter. This is a disadvantage compared to mesh-based topologies.
• dB_d,n is d-regular, each vertex is incident to d and incident from d arcs.
• The structure of necklaces depends on periodicity of strings, similarly to shuffle-exchange topology, which destroys both the symmetry and the recursivity.
• Even though the topology is not recursive, the problem how to decompose dB_2,n into isomorphic universal building blocks has been partially solved within project Galileo at JPL in Pasadena (they have built a parallel machine based on dB_2,16).
• Instead of hierarchical recursivity, de Bruijn topology has a different interesting property. dB_d,n is the line digraph of dB_d,n-1, i.e., if we replace all arcs in dB_d,n-1 with vertices and preserve adjacency, we get dB_d,n. This property is used for optimal simulations of large de Bruijn networks on small ones.
• The connectivity is nearly optimal: \kappa(dB_d,n)=\lambda(dB_d,n)=d-1. It is only d-1 due to the loops at vertices aⁿ, a in Z_d (see for example Figure).
• The fault diameter of dB_d,n is only n+1: The lengths of all d-1 vertex-disjoint paths joining two arbitrary vertices u and v are at most n+1.
• The exact value of bw_e(dB_d,n) is known up to a small constant multiplicative factor.
• The binary de Bruijn digraph dB_2,n is the state diagram of a shift register. It needs only 4 links per node to achieve the same diameter as equally sized hypercube.
• Besides digraphs, there exist also undirected graph versions. Most properties of digraphs apply to graphs, including the complexity of communication algorithms.
• Also the problem of incremental extendability and scalability was partially solved. There exist modified de Bruijn topologies, called generalized de Bruijn networks, which are incrementally extendable, and so called partial line digraphs, which are even incrementally scalable. However, the topological complexity of these variations is even higher than that of standard ones.

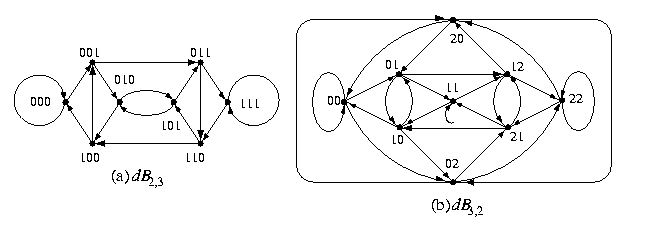
CAPTION: De Bruijn digraphs dB_2,3 and dB_3,2.

Back to the beginning of the page	Back to the CS838 class schedule

Last modified: Fri Jan 23 by tvrdik