Lecture 23: Priority Queues

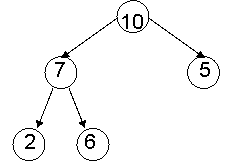
conceptual picture:

operations:

· initialize - create an empty priority queue

· insert a priority (perhaps with associated info)

· remove & return the highest priority item (& assoc. data)

· isEmpty

Example:

insert 1, 5, 10, 2, 6

then remove 5 times:

from normal queue: 1, 5, 10, 2, 6

from priority queue: 10, 6, 5, 2, 1

application: event (or task) scheduling – e.g., "To Do" list

To implement a priority queue: use a HEAP

· a balanced binary tree

height always O(log N) where N is the # of nodes

· each node has a Comparable key value

· tree has the following order and shape properties:

the order property:

for every node n,

n's key is ³ all keys in its subtrees

the shape property

1. all leaves are at depty d or d-1 (for some d)

2. all leaves at depth d are to the left of the leaves at depth d-1

3. at most one node has just one child

that child is the left child of its parent

it is the rightmost leaf at depth d

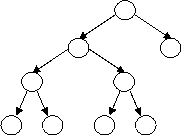
Valid heap: Valid heap shapes:

· a heap is not a BST!

Invalid heap shapes

no (leaves are at depth 2 and 4)

violates shape property 1

no (leaf at depth 2 is to the left of leaves at

depth 3 – violates property 2)

no (more than one node has just one child)

violates property 3

no (one child node is the right child)

violates property 3

no (one child is leftmost leaf at depth d)

violates property 3

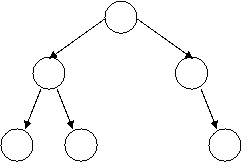
You try: which of these are heaps?

(1) (2)

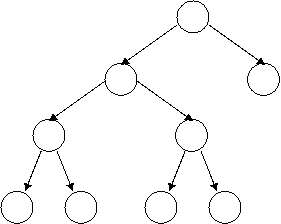
(3) (4) (5)

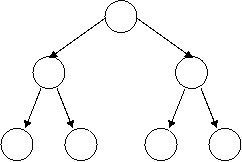
(6) (7)

Solutions yes: (2), (4), (5), (6)

no: (1), (3), (7)

More trees that have the shape property:

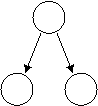
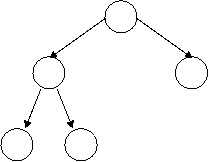
More examples

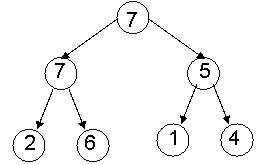
valid doesn't have the order property

Note:

· these heaps (with max at the root) are sometimes called max-heaps

· can also have min-heap (value at n is £ value of children)

To implement a heap, use an array

· each node corresponds to one position in the array

· array[0] is not used (empty or set to null)

· the root is in array[1]

· simple array indexing: for a node in array[k]

o left child is in array[2k]

o right child is in array[2k+1]

o parent is in array[k/2] - integer divide w/ truncation

Example

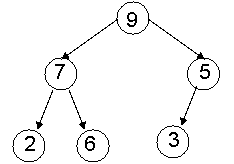
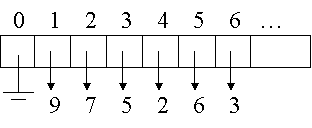
Note: shape property guarantees that there are no "holes" in the array!

Priority Queue: insert(p)

need to insert a new item (priority) so that

· heap still has the shape and order properties

· time is reasonable – i.e., O(log N) where N = # of values in the queue

step 1: add new value at the end of the array

old new

new rightmost leaf

at depth d

new leaf at depth d+1

step 2: compare new value with parent

if wrong order (child > parent) then swap

repeat up the tree until no further swaps are needed

Example: insert 8

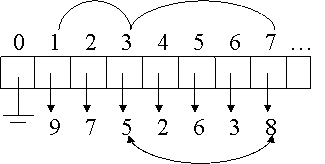
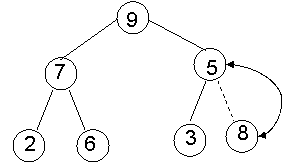
leave alone swap

You try: insert 20

2

6

7

8

9

5

20

3

0 1 2 3 4 5 6 7 8 …

9 7 8 2 6 3 5 20

solution:

Priority Queue: remove( )

· highest priority is always at array[1] (the root)

· save array[1] and return it after removing the root

· to remove the root (while keeping order and shape):

step 1:

o replace root with value at the end of the array

(rightmost leaf at depth d) –

o remove that leaf

step 2:

o if root < a child then swap with the larger child

o repeat as needed down the tree

Example:

remove ( )

(2)

(1) (3)

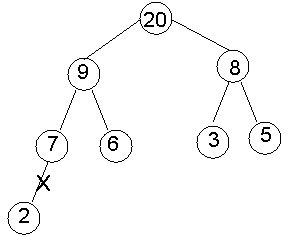
You try: remove again

Runtime efficiency for insert and remove

insert:

· add a value at the end of the array: O(1)

· swap values up the tree: worst case is all the way up

O(h) = O(log N) where N is the # of values in heap

removeMax:

· get value from root: O(1)

· replace with value at the end of the array

worst case: swap with a value at every level

O(h) = O(log N)

Note: efficiency of insert and remove for a heap

are the same as

for a priority queue implemented using a 2-3 tree,

but

· less space overhead

· much simpler to program