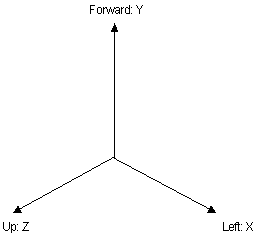
The coordinate system's x, y, z direction is define as followed
X: The cross of Y and Z to get a
Y: The branch forward direction
Z: The cross product of Y and World coordinate Up
L-system is a common way to draw tree in Graphics society. "The Algorithmic Beauty of Plants" provides detailed description about the implementation of the L-System.
Lindenmayer systems (L-systems) were conceived as a mathematical theory of plant development. The central concept of L-Systems is that of rewriting. In general, rewriting is a technique for defining complex objects by successively replacing parts of a simple initial object using a set of rewriting rules or productions. For example:
Axiom: FAB
Rules: A=F+B, B=A
1st Iteration: FAB
2nd Iteration: FF+BA
3rd Iteration: FF+AF+B
Normally, there will be a limit on the iteration. The resulting final string will be used to draw the plant or other objects depending on its interpretation of each character.
1." #" is the comment and all the context followed it will be neglected
2. The first valid line is "Recursion specification" and it should be a valid float number
3. The second valid line is "Angle specification" defined the rotation angle in turn/pitch/roll and it should be also a valid float number
4. The third valid line is "Thickness specification" defined the ratio between height and thick and it should be also a valid number represent the ratio in percentage
5. The fourth valid line is "Axiom" and it should be characters or symbols
6. The following valid line are user rules in "Char=...... " format
7. "@" denotes the end of the input
8. Example
# --- L-System
Parser/Mutator --- Lj Lapre ----------------------------------
5
18
20
c(7)"(0.25)C
C=FL>(180)L>(30)FFL>(180)L>(60)FFL>(180)L>(30)FL>(180)L>(30)FB
L=c(2)[{&&.-(30)f-(120)f+(99)"(3.205)f}]
B=c(2)[P>>W>>W>>W>>W>>W>>W>>W>>W>>W>>W]
P=FF
W=["(0.1)~(30)c(1)!(0.1).!(400)F][c(4){&&&&~.-(30)f-(120)f+(99)"(3.205)f}]
@
¡@
We first define the coordinate system used in interpreting the L-system:
|
|
The coordinate system's x, y, z direction is define as followed X: The cross of Y and Z to get a Y: The branch forward direction Z: The cross product of Y and World coordinate Up |
The turtle is a cursor that records the current processing position. The turtle will follow the following command to process and draw
Turtle Orientation commands + Rotate CCW about the Left vector +(x) Rotate x degree CCW about Left around up vector - Rotate CW about the Left vector -(x) Rotate x degree CW about the Left vector & Rotate CCW about the Up vector &(x) Rotate x degree CCW about the Up vector ^ Rotate CW about the Up vector ^(x) Rotate x degree CW about the Up vector > Rotate CCW about the forward vector >(x) Rotate x CCW about the forward vector < Rotate CW about the forward vector <(x) Rotate x CW about the forward vector Special Orientation commands | Rotate 180 deg about the Left vector % Rotate 180 deg about the up vector $ Rotatel until horizontal ~ Rotate about forward, up, and left an random degree ~(x) Rotate about forward, up, and left an random x-mean degree Movement commands in normal mode
F move forward and draw full length and draw the branch F(x) move x forward and draw and draw the branch Z move forward and draw half length and draw the branch Z(x) move x forward and draw and draw the branch Movement commands when {} active f Move forward a full distance record vertex f(x) Should not be used record vertex z Should not be used record vertex z(x) Should not be used record vertex g Move forward with full length don't record vertex g(x) Move x forward don't record vertex . Don't move record vertex Structure commands [ Push current state ] Pop current state { Start polygon shape } End polygon shape Inc/Dec commands " Multiply length with 1.1 "(x) Multiply length with x ' Multiply length with 0.9 '(x) Multiply length with x ; Multiply default angle with 1.1 :(x) Multiply angle with x also : Multiply default angle with 0.9 ;(x) Multiply angle with x also ? Multiply thickness with 1.4 ?(x) Multiply thickness with x also ! Multiply thickness with 0.7 !(x) Multiply thickness with x also t Modified with gravity which is useful when creating some tree t(x) Modified with x Additional commands c Increment color index c(x) Set color index to x @ end of object
1. I implement a line class to store the recursion, angle, thickness, axiom, and the user rule information
2. There is a LString parser used to read user file in and generated the final recursion result.
3. The L-Turtle is used to generate the shape in the maya.
The command line plug in is easy to understand and implement. The pseudo code for plug-in design is as follow.
Initialize Plug-in object: for load
Set up the command line argument
According to the argument set up the drawing Turtle class and L-String
Draw the shade in mesh
Deinitialize Plug-in object: for unload
My command line plugin provide the following arguments
| Argument Description |
Flag |
Example |
| Angle |
a |
-a Deg |
| Randomize length |
b |
-b l-rat l-dev |
| Randomize angle |
c |
-c l-rat l-dev |
| Filename |
f |
-f "U::\\Trees\\tree.LS" |
| A group of plants |
g |
-g num length width |
| Tree height |
h |
-h 0.1 ~ 10 |
| Leaf length |
l |
-l 0.1 ~ 10 |
| Mutation |
m |
-m num |
| Output Filename |
o |
-o "U::\\Trees\\tree.LS" |
| P |
p |
-p x y z |
| Recursion |
r |
-r level |
| Type |
t |
-t 0 ~ 15 |
| x position | x | -x xposition |
| y position | y | -y yposition |
| z position | z | -z zposition |
The length of each forward could determine the height of the tree and the length of each branch. In addition, the angle of each rotation could determine how the tree would be like. Thus I choose t mutate this two parameter to make trees look different even with the same kernel string. The mutation is simple
Draw-length = current-length(1 + length-ratio * Random( 0, deviation))
Draw-Angle = current-Angle(1 + Angle-ratio * Random( 0, deviation))
The randomized result will only affecting current draw won't affect the future recursion result
There are three types of mutation
1. Mutate global setting of recursion, angle, thickness
2. Mutate the axiom
3. Mutate single user rule
The setting of mutation will set up how many mutation will occur on this string. There will be a counter inside the system to adjust between the mutation of these three type. When we do mutation, the result is hard to control
I use a random generator to generate random point and each of them with certain distance limit between each other. After generating the random point, I mutate the tree's certain properties such as length, angle to produce a forest or groups of plant.
|
|
|
¡@OpenGL¡@ |
Maya |
|
¡@ |
|
¡@OpenGL¡@ |
Maya |
 |
 |
¡@Maya¡@ |
Maya |
|
|
 |
OpenGL |
¡@Maya¡@ |
 |
 |
¡@Maya¡@ |
Maya |
 |
 |
¡@Maya¡@ |
Maya |
 |
|
 |
¡@ |
|
¡@ OpenGL¡@ |
Maya |
¡@
OpenGL version: OpenGLTree.zip
Maya Command Plugin version: MayaCommandTree.zip