Prev: L10, Next: L12
Course Links: Canvas, Piazza, TopHat (212925)
Zoom Links: MW 4:00, TR 1:00, TR 2:30.
Tools
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 For visibility, you can resize all diagrams on page to have a maximum height that is percent of the screen height: .
📗 Calculator:
📗 Canvas:
pen
# Generalization Error
📗 With a large number of hidden layers and units, a neural network can overfit a training set perfectly. This does not imply the performance on new items will be good: Wikipedia.
➩ More data can be created for training using generative models or unsupervised learning techniques.
➩ A validation set can be used (similar to pruning for decision trees) to train the network until the loss (or accuracy) on the validation set begins to increase.
➩ Dropout can be used: randomly omitting units (random pruning of weights) during training so the rest of the units will have a better performance: Wikipedia.
Example
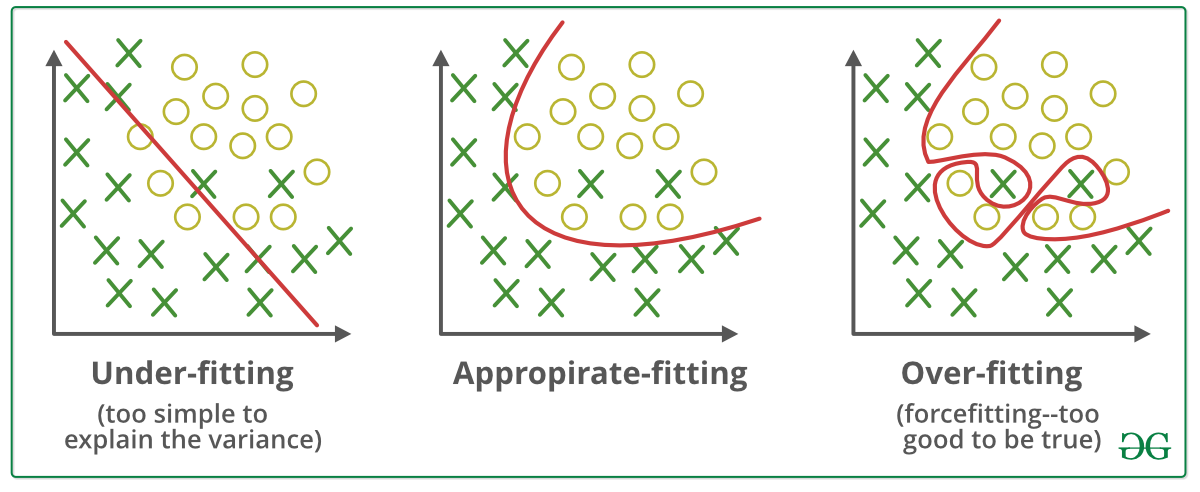
# Regularization
📗 A simpler model (with fewer weights, or many weights set to 0) is usually more generalizable and would not overfit the training set as much. A way to achieve that is to include an additional cost for non-zero weights during training. This is called regularization: Wikipedia.
➩ \(L_{1}\) regularization adds \(L_{1}\) norm of the weights and biases to the loss, or \(C = C_{1} + C_{2} + ... + C_{n} + \lambda \left\|\begin{bmatrix} w \\ b \end{bmatrix}\right\|_{1}\), for example, if there are no hidden layers, \(\left\|\begin{bmatrix} w \\ b \end{bmatrix}\right\|_{1} = \left| w_{1} \right| + \left| w_{2} \right| + ... + \left| w_{m} \right| + \left| b \right|\). Linear regression with \(L_{1}\) regularization is also called LASSO (Least Absolute Shrinkage and Selector Operator): Wikipedia.
➩ \(L_{2}\) regularization adds \(L_{2}\) norm of the weights and biases to the loss, or \(C = C_{1} + C_{2} + ... + C_{n} + \lambda \left\|\begin{bmatrix} w \\ b \end{bmatrix}\right\|^{2}_{2}\), for example, if there are no hidden layers, \(\left\|\begin{bmatrix} w \\ b \end{bmatrix}\right\|^{2}_{2} = \left(w_{1}\right)^{2} + \left(w_{2}\right)^{2} + ... + \left(w_{m}\right)^{2} + \left(b\right)^{2}\). Linear regression with \(L_{2}\) regularization is also called ridge regression: Wikipedia.
📗 \(\lambda\) is chosen as the trade-off between the loss from incorrect prediction and the loss from non-zero weights.
➩ \(L_{1}\) regularization often leads to more weights that are exactly \(0\), which is useful for feature selection.
➩ \(L_{2}\) regularization is easier for gradient descent since it is differentiable.
➩ Try \(L_{1}\) vs \(L_{2}\) regularization here: Link.
TopHat Discussion
📗 [1 points] Find the point where \(\left\|\begin{bmatrix} w_{1} \\ w_{2} \end{bmatrix}\right\| \leq d\) and minimize the cost. Use regularization.
Bound \(d\): 0.5
Cost \(C\): 0
1 slider
test rd q
📗 Notes and code adapted from the course taught by Professors Jerry Zhu, Yingyu Liang, and Charles Dyer.
📗 Content from note blocks marked "optional" and content from Wikipedia and other demo links are helpful for understanding the materials, but will not be explicitly tested on the exams.
📗 Please use Ctrl+F5 or Shift+F5 or Shift+Command+R or Incognito mode or Private Browsing to refresh the cached JavaScript.
📗 You can expand all TopHat Quizzes and Discussions: , and print the notes: , or download all text areas as text file: .
📗 If there is an issue with TopHat during the lectures, please submit your answers on paper (include your Wisc ID and answers) or this Google form Link at the end of the lecture.
📗 Anonymous feedback can be submitted to: Form.
Prev: L10, Next: L12
Last Updated: November 21, 2025 at 11:39 PM