Constant-space tunable-accuracy insertion-robust learned range indices.

Spring 2020. [A class project; CS 839: Advanced Database Systems]

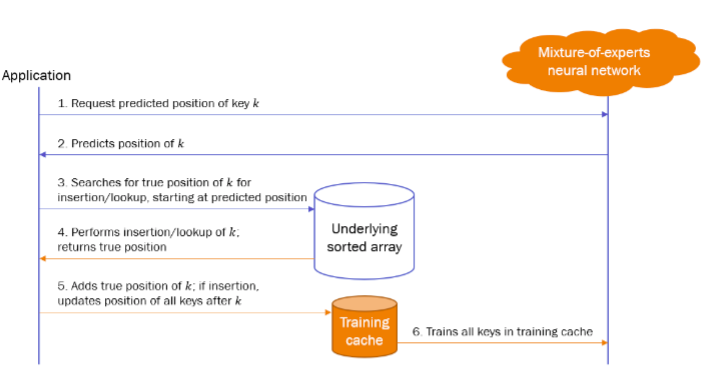
B-tree is a data structure that permits mapping a key to its position in a sorted array of keys. It is a cumulative distribution function (CDF) of a sample space of keys. The learned range index (Kraska et al., 2018) proposes the use of a machine learning model to approximate the CDF of the key space. One of the main limitations of the original learned index framework as proposed in (Kraska et al.,2018) is that it assumes the underlying data distribution (key space) to be static, which implies that a learned range index does not support any form of insertions or deletions in the key space. We address this challenge by extending the learned range index to accommodate a dynamic data distribution. Our learned index architecture accounts for various insertion and lookup patterns, by using a mixture-of-experts model trained on a training cache of recently accessed keys, and a feedback mechanism that allows the learned range index to optimize for different data access patterns. Furthermore, we analyze various conditions and parameter settings that affect the accuracy of our learned range index architecture, and show that our architecture has a tunable accuracy that allows for trading off space consumption.

If you want the report, shoot me an email.

---

A Learned Index: Optimizing Search and Insert Operations on a B-Tree Structure

Fall 2020. [A class project; CS 764: Topics in Database Management Systems]

B-trees are used prolifically as indices for databases since they achieve good lookup performance in many scenarios by subdividing the key distribution recursively. Traditionally, each node in a B-tree is sorted to enable fast searching; however, production implementations of B-trees in commercial databases do not take good advantage of this fact, as they only use elementary search algorithms, such as binary search and sequential search, within B-tree nodes. We seek to improve the performance of the insert and lookup operations in B-trees in a way that responds to the key distribution within each B-tree node without incurring the overhead of more heavy-handed approaches, such as learned indices. We present a new algorithm that makes a variety of improvements to the canonical B-tree structure. Namely, the B*DASS index uses (1) a gapped array in each B-tree node to maintain performance in the presence of nonlinear key distributions, (2) piecewise linear interpolation within each node to achieve greater initial search accuracy, enabling larger node array sizes, (3) a single marker within each node to indicate the most suitable number of interpolation points, and (4) a feedback mechanism to ensure that the lookup operation responds to poorly performing searches on frequently looked-up keys. After discussing the theoretical basis of these optimizations, we present a working implementation, which we call the B*DASS tree index, and gather performance benchmark data to compare our algorithm favorably against binary search and vanilla linear interpolation search.