Next: Infinite Cache, Finite Request
Up: On the Implications of
Previous: Trace Characteristics
Consider a cache that receives a stream of requests for Web pages.
Let N be the total number of Web pages in the universe.
Let PN(i) be the conditional probability that, given the arrival of
a page request, the arriving request is made for page i.
Let all the pages be ranked in order of their popularity where
page i is the i'th most popular page.
We assume that PN(i), defined for 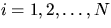 , has a
``cut-off'' Zipf distribution given by
, has a
``cut-off'' Zipf distribution given by
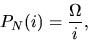
where
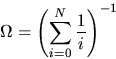
Each page request is drawn independently from the Zipf distribution,
so we are neglecting any other source of correlations in
the request stream. Moreover, we assume that, over the course of time,
no pages are invalidated by the cache. We realize
that this is an artificial model, but
our goal here is to ask what results we can obtain from such a simple
assumption.
We calculate the hit-ratio for the cache in two extreme limiting
cases and the interrival times in a limiting case, which we consider
in the following three sections.
Pei Cao
6/2/1998
![]()